Derivace funkce Pednka 2 Smrnice seny funkce f

![Směrnice sečny funkce f procházející body [a, f(a)] a [b, f(b)] ¡ ¡ poměrná Směrnice sečny funkce f procházející body [a, f(a)] a [b, f(b)] ¡ ¡ poměrná](https://slidetodoc.com/presentation_image_h/a959ab04e9d67262f027d4a29372b234/image-2.jpg)






































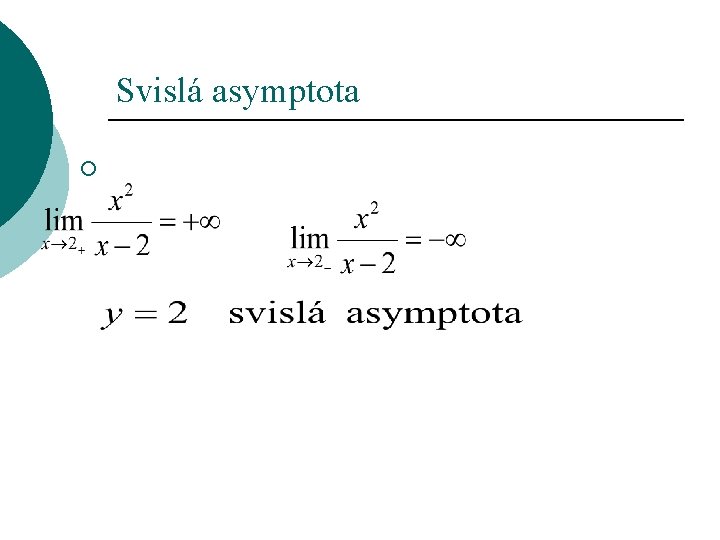





















- Slides: 78

Derivace funkce Přednáška 2
![Směrnice sečny funkce f procházející body a fa a b fb poměrná Směrnice sečny funkce f procházející body [a, f(a)] a [b, f(b)] ¡ ¡ poměrná](https://slidetodoc.com/presentation_image_h/a959ab04e9d67262f027d4a29372b234/image-2.jpg)
Směrnice sečny funkce f procházející body [a, f(a)] a [b, f(b)] ¡ ¡ poměrná diference s diferenčním krokem h=b-a Směrnice tečny k funkci f v bodě [a, f(a)]

Derivace funkce v bodě x 0 Nechť f je definována v nějakém , potom pokud existuje vlastní nebo nevlastní nazveme ji derivací funkce f v bodě Označení ¡ Ekvivalentní zápis

Derivace zprava a zleva ¡ derivace v bodě existuje, pokud existují jednostranné derivace v bodě a mají stejnou hodnotu. ¡ ¡ ¡ Lokální pojem Globální pojem

Příklad ¡ Jednostranné derivace funkce f(x)=|x|, kde x 0 =0 ¡ Derivace funkce f(x)=|x| v x 0 =0 neexistuje ¡

Derivace funkce xn

Derivace základních funkcí ¡ k je konstanta

Vlastnosti derivace Pokud funkce mají v bodě x vlastní derivaci, potom také má v bodě x vlastní derivaci a platí ¡

Příklad ¡ Zderivujte funkci

Příklad ¡ Zderivujte funkci

Derivace složené funkce ¡ Jestliže funkce je diferencovatelná v bodě a funkce f je diferencovatelná v bodě , potom složená funkce , je diferencovatelná v bodě x a platí: ¡ Derivace vyšších řádů

Příklady ¡ Zderivujte funkci ¡ Spočtěte druhou derivaci funkce

Ekonomický význam derivace ¡ Průměrný poměr změny funkce f(x) ¡ Okamžitý poměr změny funkce f(x)

l’Hospitalovo pravidlo Nechť f a g jsou spojité na nějakém okolí bodu c a nechť nebo Potom ¡ Rovnice tečny Má-li funkce v bodě x=a derivaci, potom tečna ke grafu funkce y=f(x) s dotykovým bodem A=[a, f(a)] má analytické vyjádření y- f(a)= f(a)´(x-a).

Příklad Najděte rovnici tečny grafu funkce ¡ f: y = ex - e-x v bodě T[0, ? ]. ¡

Elasticita funkce ¡ Elasticita funkce f(x) je číslo, které udává míru schopnosti závisle proměnné reagovat na změny nezávisle proměnné x. ¡ Elasticita funkce f(x) v bodě x je číslo E(x), které udává poměr procentuální změny závisle proměnné y k jednoprocentuální změně nezávisle proměnné x

Elasticita funkce poptávky

Mezní příjmy a mezní náklady Celkový příjem TR(Q) ¡ Mezní příjem MR(Q)= TR`(Q) ¡ Celkové náklady TC(Q) ¡ Mezní náklady MC(Q)= TC`(Q) ¡

Extrémy funkce na množině ¡ Definice: Funkce f nabývá na množině M svého maxima Funkce f nabývá na množině M svého minima ¡ Funkce f nabývá na množině M ostrého maxima ¡ Funkce f nabývá na množině M ostrého minima ¡

Základní vlastnosti spojitých funkcí Vlastnost: Nechť f je spojitá na uzavřeném intervalu , potom f je omezená na . ¡ Vlastnost: Nechť f je spojitá na uzavřeném intervalu , potom f nabývá maxima (minima) v . ¡ Vlastnost: Nechť f je spojitá na uzavřeném intervalu a nechť a (resp. a ) , potom existuje bod , že ¡

vztah vlastní derivace a spojitosti funkce Jestliže funkce f má vlastní derivaci v bodě , potom funkce f je v tomto bodě spojitá. ¡ Definice: Řekneme, že funkce f, definovaná na nějakém okolí bodu , má v bodě c ostré lokální maximum (ostré lokální minimum), jestliže

Vlastnosti lokálních extrémů a derivace Vlastnost I. : Má-li funkce f v bodě c lokální extrém a existujeli , pak . ¡ Vlastnost II. : Jestliže a jestliže , potom má funkce f v bodě c ostrý lokální extrém. A to pro ostré lokální minimum, resp. pro ostré lokální maximum. ¡ Vlastnost III. : Nechť a . Jestliže n je sudé, potom f má v bodě c ostrý lokální extrém a to ostré lokální maximum v případě, že nebo ostré lokální minimum v případě, že . Jestliže n je liché, potom v c lokální extrém nemá. ¡

Jak této vlastnosti využít ke zjišťování extrémů funkce f? ¡ ¡ ¡ ¡ Vyšetříme definiční obor funkce Funkci f zderivujeme Derivaci položíme rovnu 0 Nalezneme všechna x, pro která je splněna rovnice Podezřelé body z extrému Nalezneme druhou derivaci funkce f a podezřelé body z extrému dosadíme do druhé derivace funkce f Extrém nastává v těch bodech, ve kterých je druhá derivace funkce f nenulová Rozhodneme, zda se jedná o lokální maximum či lokální minimum

Příklad 1 ¡ Nalezněte lokální extrémy funkce

Příklad 2 ¡ Zjistěte, zda funkce má v bodě lokální extrém, a jaký. ¡ Lokální minimum

Extrémy funkce na intervalu I Funkce definovaná na intervalu I může mít extrémy: ¡ Ve vnitřních bodech intervalu I, v nichž je derivace nulová, ¡ Ve vnitřních bodech intervalu I, v nichž první derivace neexistuje, ¡ V bodech, které jsou krajní body intervalu I (pokud I je uzavřený nebo polouzavřený interval) ¡

Vztah derivace funkce a monotonie funkce ¡ ¡ ¡ Vlastnost IV. : Buď f definovaná na intervalu I a Je-li pro , pak funkce f je rostoucí na . Je-li pro , pak funkce f je klesající na .

Jak vyšetřit intervaly monotonie? A mohu zjistit při vyšetřování intervalů monotonie lokální extrémy funkce f? ¡ ¡ ¡ ¡ ¡ Určíme definiční obor funkce f Funkci f zderivujeme Derivaci položíme rovnu 0 Nalezneme všechna x, pro která je splněna rovnice Tyto body rozsekají definiční obor funkce na menší intervaly V každém z těchto intervalů vezmeme libovolný vnitřní bod a dosadíme ho do předpisu první derivace funkce f. Pokud je hodnota první derivace funkce f v tomto vnitřním bodě kladná, pak je funkce f rostoucí na celém tomto intervalu Pokud je hodnota první derivace funkce f v tomto vnitřním bodě záporná, pak je funkce f klesající na celém tomto intervalu V krajních bodech intervalů monotonie, ve kterých se funkce mění z rostoucí na klesající nastává lokální maximum V krajních bodech intervalů monotonie, ve kterých se funkce mění z klesající na rostoucí nastává lokální minimum

Příklad 3 ¡ Vyšetřete intervaly monotonie funkce


Konvexní a konkávní funkce Definice: Řekneme, že funkce f je na intervalu I ryze konvexní leží pod spojnicí bodů ¡ konvexní leží pod nebo na spojnici bodů ¡ ryze konkávní leží nad spojnicí bodů ¡ konkávní leží nad nebo na spojnici bodů ¡

Vztah intervalů konkavity a konvexity funkce a derivace funkce Vlastnost: Nechť funkce f je spojitá na intervalu a nechť , potom funkce f je ryze konvexní na . ¡ Jestliže funkce f je spojitá na intervalu a nechť ¡ ¡ , potom funkce f je ryze konkávní na .

Jak najít intervaly konkavity a konvexity? ¡ ¡ ¡ ¡ Vyšetříme definiční obor funkce f Nalezneme druhou derivaci funkce f Nalezneme všechna x, pro která je splněna rovnice Tyto body rozsekají definiční obor funkce na menší intervaly V každém z těchto intervalů vezmeme libovolný vnitřní bod a dosadíme ho do předpisu druhé derivace funkce f. Pokud je hodnota druhé derivace funkce f v tomto vnitřním bodě kladná, pak je funkce f konvexní na celém tomto intervalu Pokud je hodnota druhé derivace funkce f v tomto vnitřním bodě záporná, pak je funkce f konkávní na celém tomto intervalu

Příklad ¡ Nalezněte intervaly, v nichž je funkce ¡ konvexní a konkávní.

příklad ¡

Inflexní bod Definice: Nechť existuje . Řekneme, že funkce f má v bodě c inflexi (c je bodem inflexe funkce f ), jestliže a tak, že f je konkávní (resp. konvexní) v a konvexní (resp. konkávní) v Vlastnost I. : Jestliže a c je bodem inflexe, potom . Vlastnost II. : Jestliže a , potom má funkce f v bodě c inflexi. ¡

Asymptoty grafu funkce Definice : Přímku p nazveme asymptotou grafu funkce f(x), jestliže limita vzdálenosti bodu [x, f(x)]grafu funkce od přímky p je nula. ¡ Vlastnost: Přímka o rovnici x=a je svislou asymptotou grafu funkce f(x), právě když nastává alespoň jedna ze čtyř možností: ¡ nebo ¡

Šikmá asymptota grafu funkce Přímka o rovnici y=kx+q je šikmou asymptotou grafu funkce f(x), právě když nastává alespoň jedna ze dvou možností: ¡ a zároveň ¡ nebo ¡ a zároveň ¡

Příklad: Určete asymptoty ke grafu funkce f: y = x 2(x - 2)-1 ¡ Šikmá asymptota

Výpočet q ¡
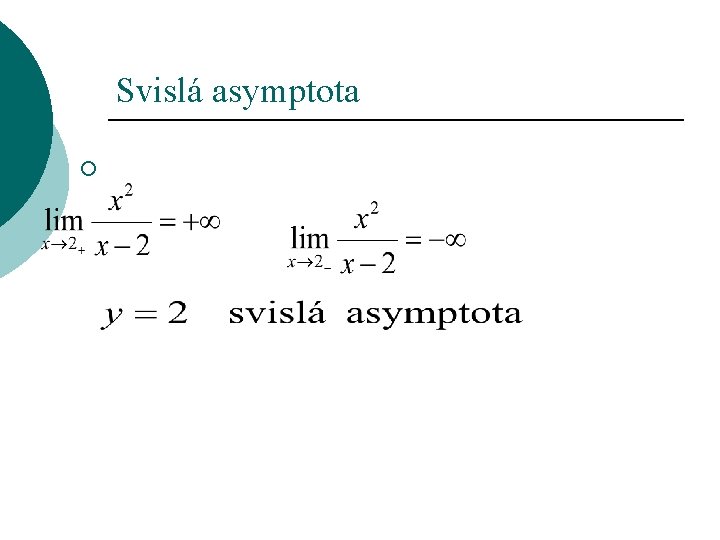
Svislá asymptota ¡

Užití derivace k minimalizaci průměrných nákladů a maximalizaci celkových příjmů ¡ Průměrné náklady ¡ Lokální extrém ¡ Množství Q 0, které zaručuje minimální průměrné náklady, je hodnota, ve které se mezní náklady vyrovnají průměrným nákladům.

Maximalizace zisku ¡ ¡ ¡ Funkce zisku Hledání lokálního maxima Množství Q 0, ve kterém dochází k maximalizaci zisku je hodnota, ve které se mezní náklady rovnají mezním příjmům.

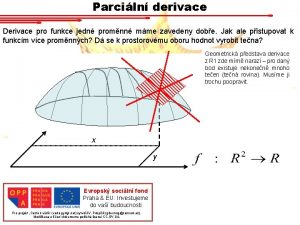
Funkce více proměnných

Funkce více proměnných ¡ ¡ ¡ Bod v rovině Bod v Graf funkce v plocha Graf funkce v Vzdálenost dvou bodů v rovině

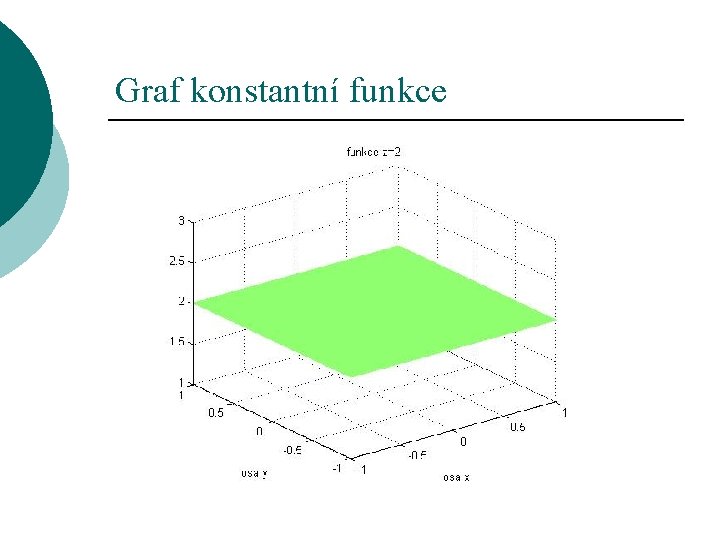
Graf konstantní funkce

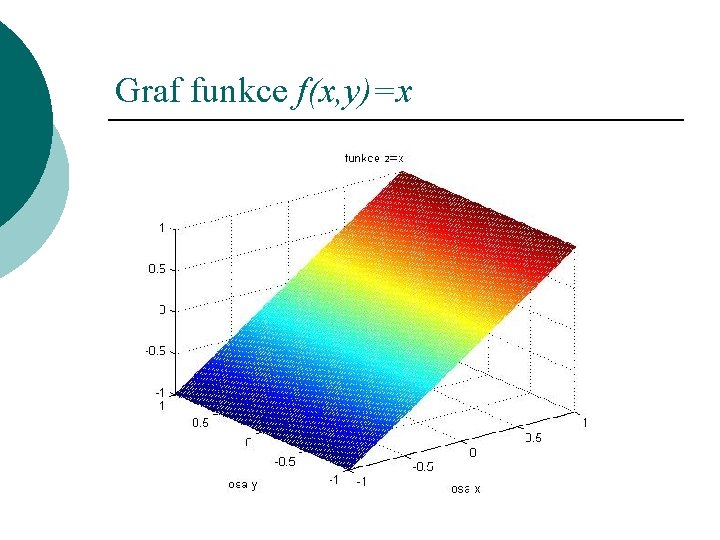
Graf funkce f(x, y)=x ¡

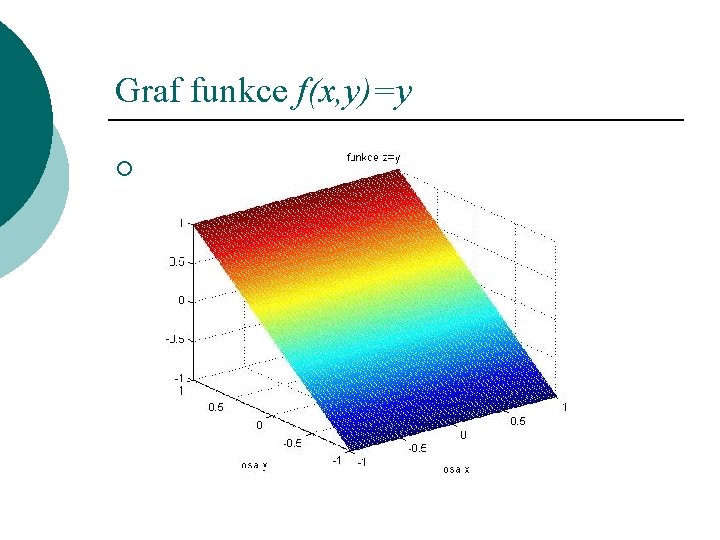
Graf funkce f(x, y)=y ¡

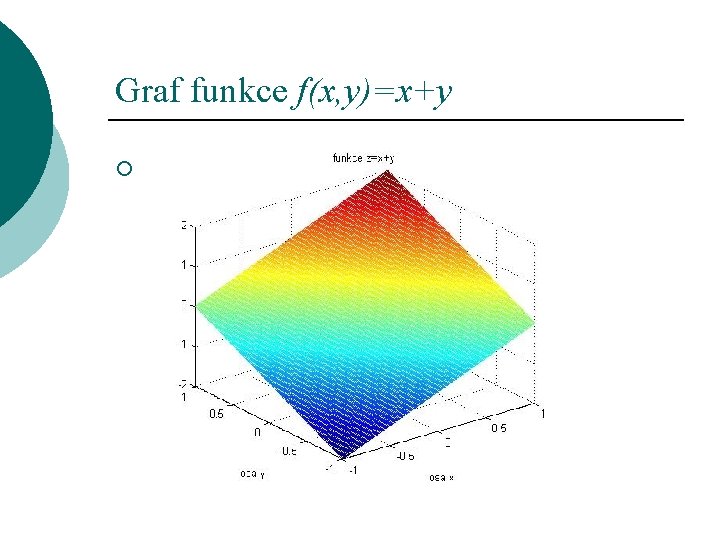
Graf funkce f(x, y)=x+y ¡

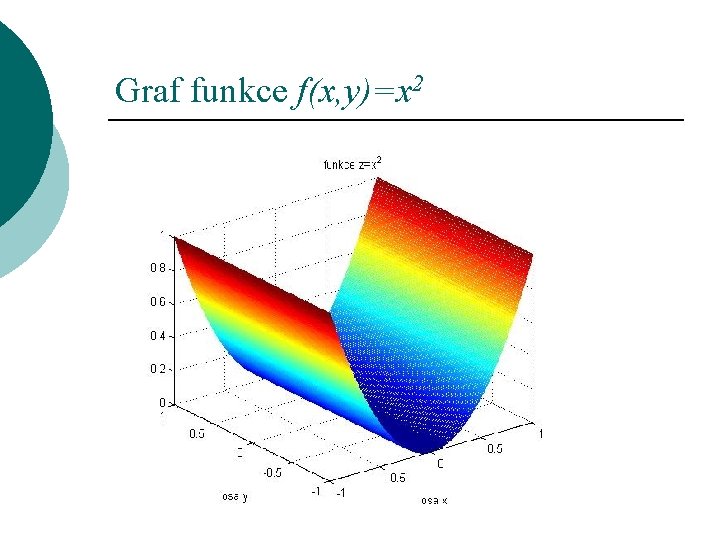
Graf funkce f(x, y)=x 2 ¡

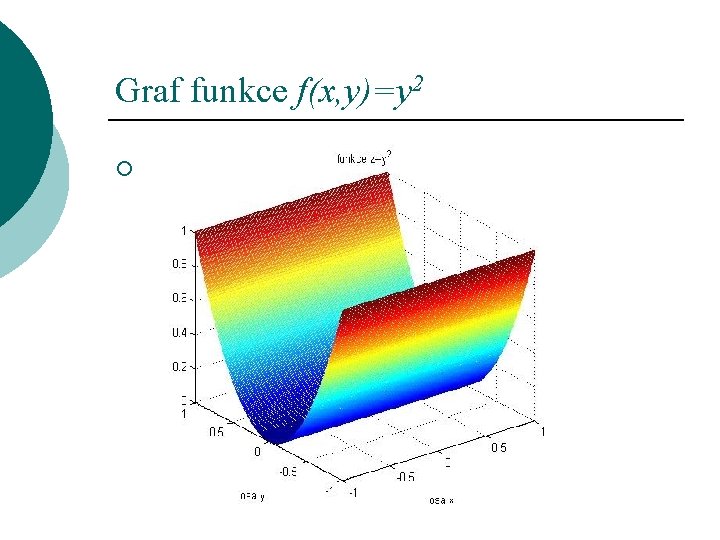
Graf funkce f(x, y)=y 2 ¡

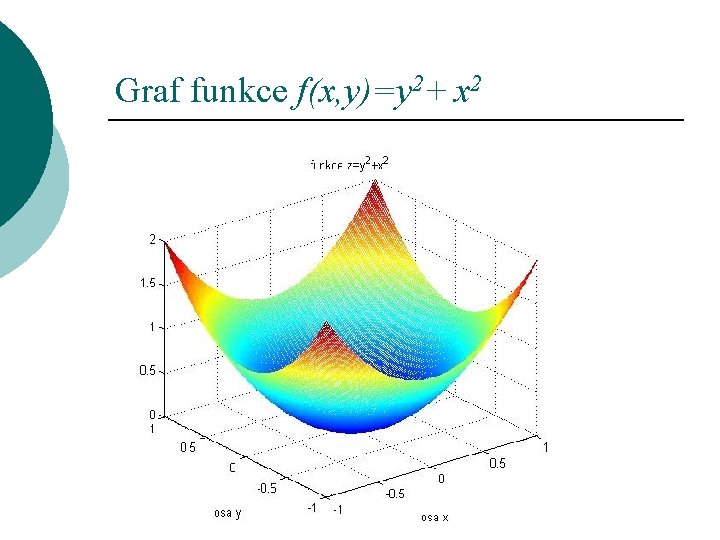
Graf funkce f(x, y)=y 2+ x 2 ¡

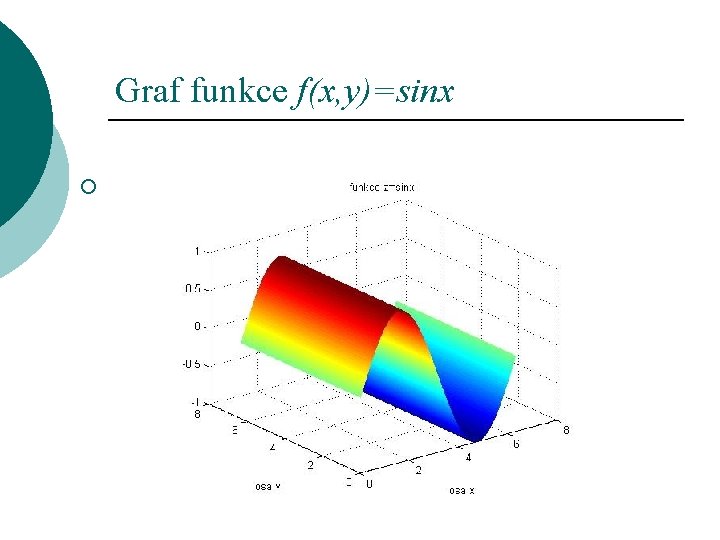
Graf funkce f(x, y)=sinx ¡

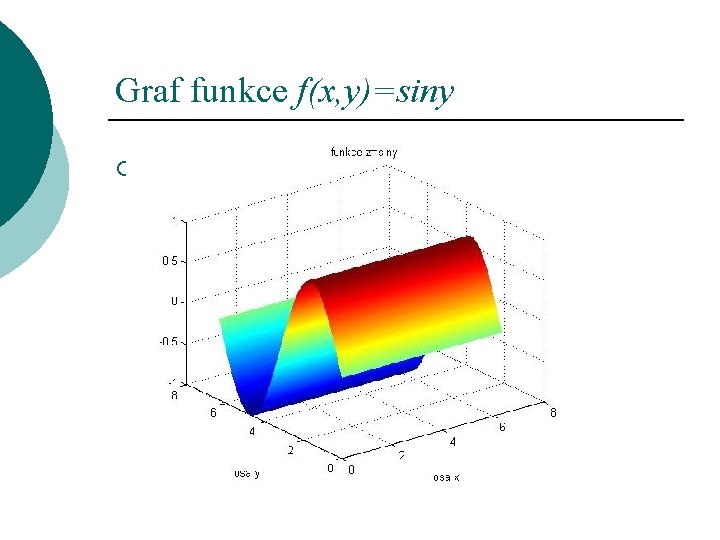
Graf funkce f(x, y)=siny ¡

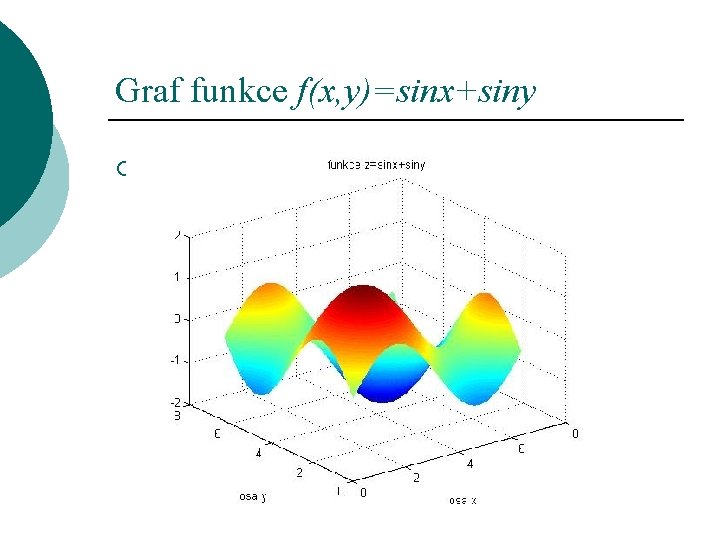
Graf funkce f(x, y)=sinx+siny ¡

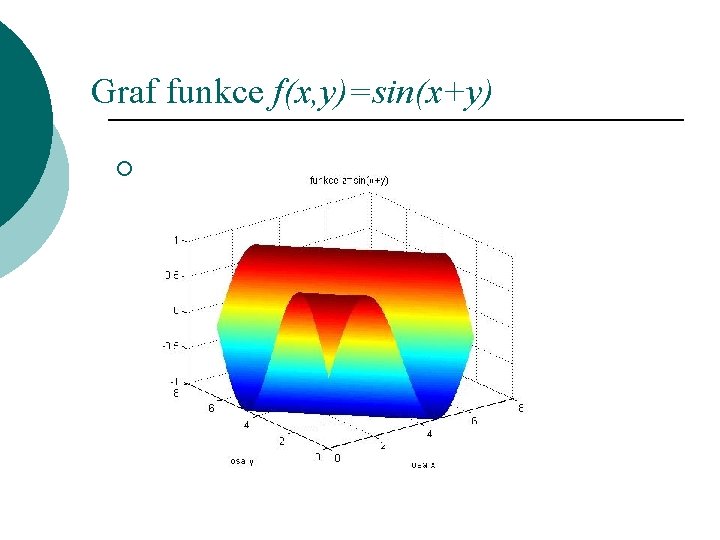
Graf funkce f(x, y)=sin(x+y) ¡

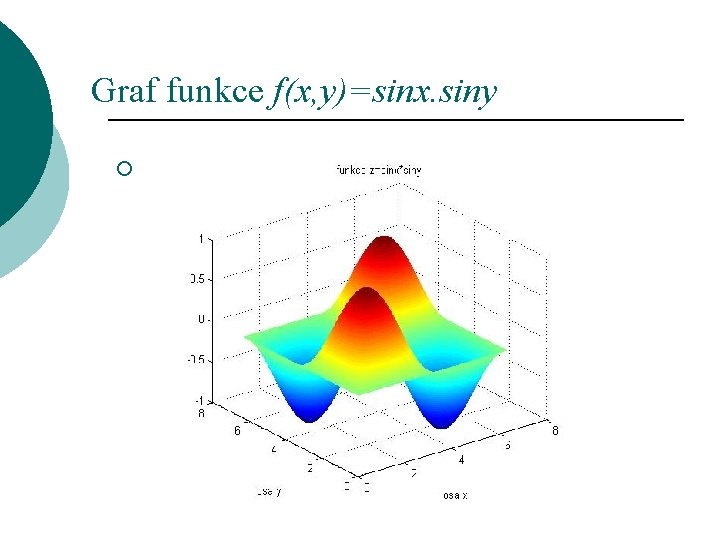
Graf funkce f(x, y)=sinx. siny ¡

Graf funkce f(x, y)=x. y ¡

Graf funkce f(x, y)=x. siny ¡

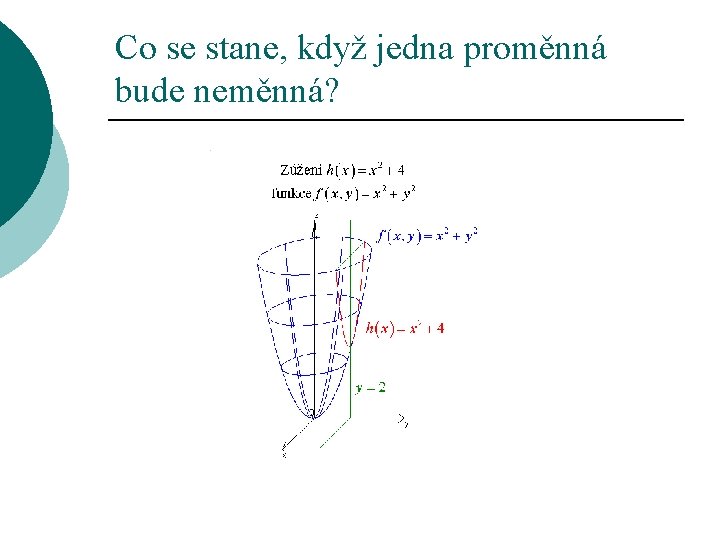
Co se stane, když jedna proměnná bude neměnná?

Parciální derivace podle x ¡ ¡ Proměnnou y zafixuji. Pak f(x, y)=φ(x) Parciální derivace funkce f(x, y) podle x v bodě A=[x 0, y 0 ] je směrnice tečny ke grafu funkce φ(x) v bodě A=[x 0, y 0 ]

Parciální derivace podle y Proměnnou x zafixuji. Pak f(x, y)=ψ(y) Parciální derivace funkce f(x, y) podle y v bodě A=[x 0, y 0] je směrnice tečny ke grafu funkce ψ(y) v bodě A=[x 0, y 0]

Derivace funkce více proměnných Definice: Derivací funkce v bodě nazveme vektor parciálních derivací této funkce v bodě A. ¡ Nazývá se také gradient funkce. ¡ Geometricky- směr největšího růstu funkce f v okolí bodu A ¡ Definice: Funkce se nazývá hladká v bodě A, jestliže všechny parciální derivace v bodě A existují a jsou spojité. ¡

Příklad ¡ Vypočtěte parciální derivace podle obou proměnných funkce

Parciální derivace vyšších řádů ¡ ¡ ¡ smíšené derivace Vlastnost: Pokud jsou smíšené derivace ( , ) spojité funkce v bodě potom platí = .

Příklad ¡ Vypočtěte druhé parciální derivace funkce

Užití v mikroekonomii ¡ Funkce užitku ¡ je mezní užitek spotřebního statku x 1 a udává, jak se změní užitek v důsledku jednotkové změny prvního spotřebního statku při nezměněné úrovni druhého spotřebního statku ¡ je mezní užitek spotřebního statku x 2 a udává, jak se změní užitek v důsledku jednotkové změny druhého spotřebního statku při nezměněné úrovni prvního spotřebního statku

Lokální a globální extrémy funkcí více proměnných ¡ Definice: V bodě nastává maximum funkce vzhledem k množině M, platí-li

Lokální a globální extrémy funkcí více proměnných ¡ ¡ V bodě nastává minimum funkce vzhledem k množině M, platí-li pro všechna

Lokální a globální extrémy funkcí více proměnných ¡ Značíme Pokud množina globální extrémy ¡ Pokud množina nebo ………lokální extrémy ¡ Body z , v nichž může nastat extrém funkce f, budeme nazývat stacionární body ¡

Nutná podmínka pro extrém Jestliže funkce má v bodě extrém, potom pro každé platí buď nebo neexistuje. ¡

Postačující podmínka pro lokální extrém Jestliže funkce má v bodě ¡ pro každé f má spojitou druhou derivaci v bodě a ¡ pak má funkce v bodě lokální extrém.

A to lokální maximum, jestliže v bodě , lokální minimum, jestliže v bodě , ¡

Sedlový bod Jestliže nemá funkce v bodě lokální extrém, bod se nazývá sedlovým bodem. ¡ Funkce f(x, y)=x 2 -y 2

Příklad Nalezněte lokální extrémy funkce ¡ stacionární bod ¡ ¡ Sedlo v

Příklad ¡ Nalezněte lokální extrémy funkce stacionární body ¡ lok. max ¡ Lok. min

graf

Globální extrémy funkce více proměnných na kompaktní množině ¡ ¡ ¡ Kompaktní množina-omezená a uzavřená množina. Extrémy mohou nastat : v bodech, ve kterých jsou všechny první parciální derivace rovny nule v bodech, ve kterých některé parciální derivace neexistují a zbývající první parciální derivace rovny nule v hraničních bodech definičního oboru. Z těchto podezřelých bodů vybereme ty s největší (nejmenší) funkční hodnotou. V těchto bodech nastává globální maximum (minimum).
 Tabulka derivace
Tabulka derivace Jak vypočítat cotg na kalkulačce
Jak vypočítat cotg na kalkulačce Monotonie funkce
Monotonie funkce Mocninné funkce s celočíselným exponentem
Mocninné funkce s celočíselným exponentem Sinus trojúhelník
Sinus trojúhelník Funkce cotangens
Funkce cotangens Typy rodin
Typy rodin Funkce managementu
Funkce managementu Broccovo centrum
Broccovo centrum Trigonometrie
Trigonometrie Wilsonovy svody
Wilsonovy svody Sql datumové funkce
Sql datumové funkce Konstantní funkce
Konstantní funkce Humanizační funkce kultury
Humanizační funkce kultury Defertova funkce
Defertova funkce Definice funkce matematika
Definice funkce matematika Tangens z 30
Tangens z 30 Ppady
Ppady Hektokotylové rameno funkce
Hektokotylové rameno funkce Letní lodyha funkce
Letní lodyha funkce Erytropoetin funkce
Erytropoetin funkce Minimalizace logické funkce
Minimalizace logické funkce Pr��ce dom�� kompletace
Pr��ce dom�� kompletace Goniometrické funkce ostrého úhlu
Goniometrické funkce ostrého úhlu Investiční funkce
Investiční funkce Lineární funkce
Lineární funkce Model mezičasové volby
Model mezičasové volby Kognitivní schopnosti
Kognitivní schopnosti Co je podnik
Co je podnik Funkce rodiny
Funkce rodiny Lagrangeova funkce
Lagrangeova funkce Funkce a jejich vlastnosti
Funkce a jejich vlastnosti Manifestní a latentní funkce
Manifestní a latentní funkce Sudost lichost funkce
Sudost lichost funkce Dvoulící list
Dvoulící list Agramatizmy
Agramatizmy Konvexnost
Konvexnost Hroznovitý stonek
Hroznovitý stonek Vzorec vrchol paraboly
Vzorec vrchol paraboly Co je to radula
Co je to radula Erytropoetin funkce
Erytropoetin funkce Typy trhů
Typy trhů Word funkce
Word funkce Sinova a cosinova věta
Sinova a cosinova věta Goniometrické funkce ostrého úhlu
Goniometrické funkce ostrého úhlu Lineární funkce
Lineární funkce Funkce když excel
Funkce když excel Ethanamid
Ethanamid Výtrusný klas
Výtrusný klas Definice obchodu
Definice obchodu Eulerova funkce
Eulerova funkce Pankreas funkcia
Pankreas funkcia Kreditní funkce finančního trhu
Kreditní funkce finančního trhu Kvadratické funkce
Kvadratické funkce Funkce - teorie
Funkce - teorie Stavba mozku
Stavba mozku Funkce rodiny pracovní list
Funkce rodiny pracovní list Goniometrické funkce tabulka
Goniometrické funkce tabulka Kvadratická funkce vlastnosti
Kvadratická funkce vlastnosti Funkce daní
Funkce daní Hektokotylové rameno funkce
Hektokotylové rameno funkce Určete definiční obor funkce
Určete definiční obor funkce Skeletizace
Skeletizace Literární žánr
Literární žánr Tangensoida
Tangensoida Analza
Analza Graf lineární funkce
Graf lineární funkce Organa genitalia masculina
Organa genitalia masculina Kkkq
Kkkq Goniometrické funkce prezentace
Goniometrické funkce prezentace Rolandova rýha
Rolandova rýha Mezimozek
Mezimozek Slidetodoc.com
Slidetodoc.com