Funkce Linern funkce Definice linern funkce Linern funkce

Funkce Lineární funkce

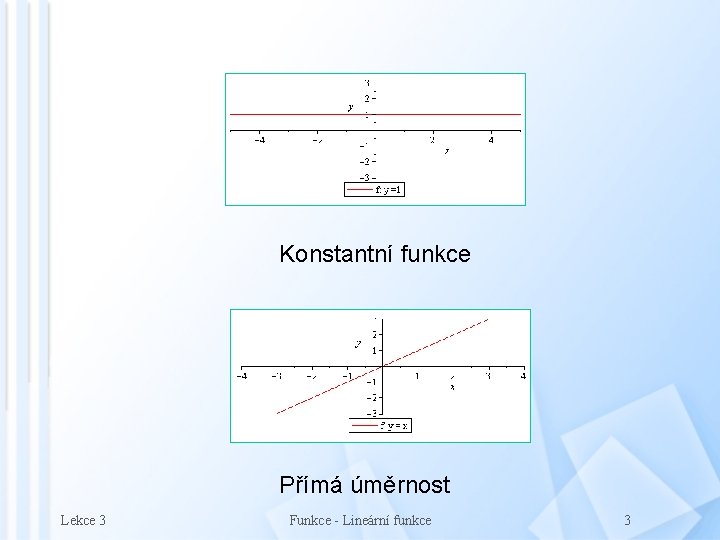
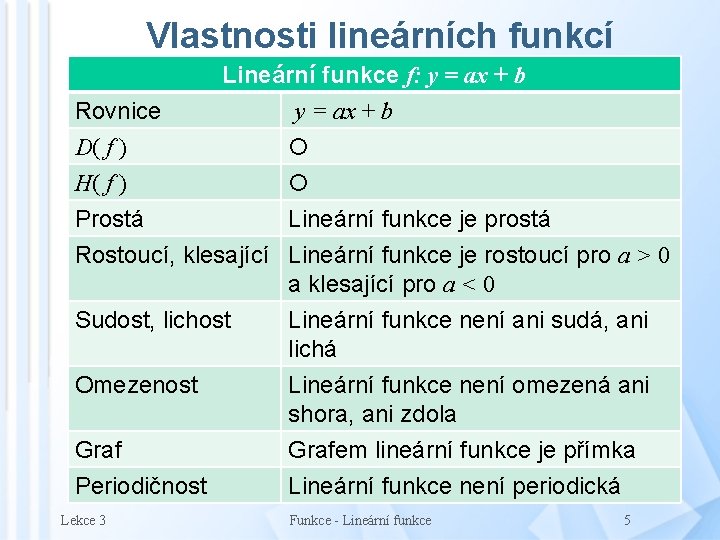
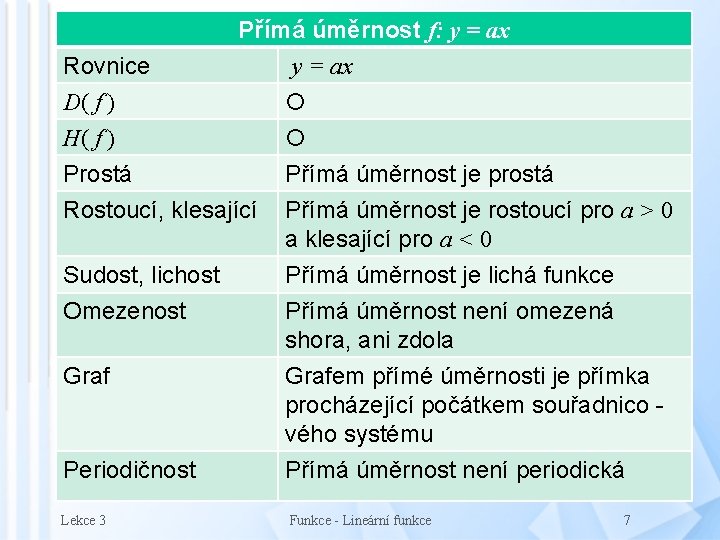
Definice lineární funkce Lineární funkce je každá funkce f na množině (tj. funkce o definičním oboru , která je dána předpisem f: y = ax + b, kde a, b jsou reálná čísla Speciální případy lineárních funkcí Ø Prvním speciálním případem lineární funkce je funkce s koeficientem a = 0, tj. funkce f: y = b, kterou nazýváme konstantní funkce Ø Druhým speciálním případem lineární funkce je funkce s koeficientem b = 0 a a ≠ 0, tj. funkce f: y = ax, kterou nazýváme přímá úměrnost Grafem lineární funkce je přímka Lekce 3 Funkce - Lineární funkce 2

Konstantní funkce Přímá úměrnost Lekce 3 Funkce - Lineární funkce 3

Vliv koeficientů na graf funkce Je-li dána lineární funkce tvaru f: y = ax + b, pak platí: Ø Ø Ø Je-li b = 0, přímka vždy prochází počátkem souřadnicového systému (bodem [0; 0]) Je-li b ≠ 0 graf lineární funkce prochází bodem na ose y rovnající se hodnotě b Je-li a > 0, jedná se o graf rostoucí funkce Je-li a < 0, jedná se o klesající funkci Je-li a = 0, není lineární funkce prostá Graf funkce f: y = ax bude osově souměrný podle osy y s funkcí g: y = – ax Lekce 3 Funkce - Lineární funkce 4

Vlastnosti lineárních funkcí Rovnice D( f ) H( f ) Lineární funkce f: y = ax + b Prostá Lineární funkce je prostá Rostoucí, klesající Lineární funkce je rostoucí pro a > 0 a klesající pro a < 0 Sudost, lichost Omezenost Graf Periodičnost Lekce 3 Lineární funkce není ani sudá, ani lichá Lineární funkce není omezená ani shora, ani zdola Grafem lineární funkce je přímka Lineární funkce není periodická Funkce - Lineární funkce 5

Rovnice D( f ) H( f ) Lineární konstantní funkce f: y = b y=b Prostá Rostoucí, klesající Sudost, lichost {b} Konstantní funkce není prostá Konstantní funkce není ani rostoucí, ani klesající Konstantní funkce je sudá Omezenost Konstantní funkce je omezená shora i zdola Grafem konstantní funkce je přímka rovnběžná s osou x Periodičnost Konstantní funkce je periodická, ale nelze určit základní periodu Lekce 3 Funkce - Lineární funkce 6

Rovnice D( f ) H( f ) Přímá úměrnost f: y = ax Prostá Rostoucí, klesající Přímá úměrnost je prostá Přímá úměrnost je rostoucí pro a > 0 a klesající pro a < 0 Sudost, lichost Přímá úměrnost je lichá funkce Omezenost Graf Přímá úměrnost není omezená shora, ani zdola Grafem přímé úměrnosti je přímka procházející počátkem souřadnico vého systému Periodičnost Přímá úměrnost není periodická Lekce 3 Funkce - Lineární funkce 7

Zadání lineární funkce Lineární funkce může být zadána: Ø Funkčním předpisem Ø Dvěma různými body ► Řešíme pomocí soustavy lineárních rovnic. Souřadnice [x; y] dvou bodů musí vyhovovat rovnici y = ax + b, za x a y dosadíme souřadnice bodů. Získáme soustavu dvou lineárních rovnic pro dvě neznámé a, b. Po vyřešení dosadíme a, b do předpisu lineární funkce Ø Grafem Lekce 3 Funkce - Lineární funkce 8