Funkce Funkce definice Funkce je zobrazen kter kadmu

Funkce

Funkce - definice Funkce je zobrazení, které každému číslu z podmnožiny reálných čísel R přiřazuje právě jedno reálné číslo. Funkci značíme písmeny f, g, h, … a zapisujeme ve tvaru: y = f(x), např. y = 2 x+1 nebo ve tvaru: f: y = 2 x + 1 kde proměnná x je argument funkce.

Definiční obor f: y = 2 x + 1 kde proměnná x je argument funkce, nebo-li nezávisle proměnná. Nezávislost je dána tím, že její hodnotu můžeme libovolně měnit, ovšem Množina všech přípustných hodnot argumentu jen v rámci definované x, množiny, proměnná definičního tedy všechny hodnoty, kterých může x oboru. pro danou funkci nabývat, se nazývá definiční obor. Značí se: D(f)

Obor hodnot Ke všem přípustným hodnotám argumentu x přísluší právě jedna funkční hodnota. Ty všechny dohromady tvoří obor hodnot (obor funkčních hodnot). Funkční hodnota neboli závisle proměnná je číslo, které funkce přiřadí konkrétnímu argumentu x. Jinak řečeno: výstupní hodnota funkce. Obvykle ji značíme y nebo f(x). Hodnota závisle proměnné je pro danou Obor hodnot je množina všech reálných čísel, které funkci jednoznačně určena hodnotouf, jestliže dostaneme jako výstupní hodnotu funkce argumentu x za x dosadíme všechny přípustné hodnoty z D(f). (výpočtem) - proto „závisle“ proměnná. Značí se: H(f)

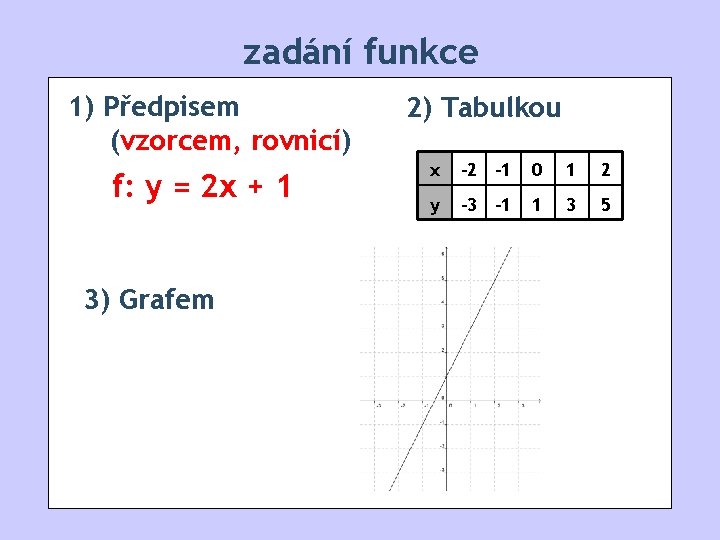
zadání funkce 1) Předpisem (vzorcem, rovnicí) f: y = 2 x + 1 3) Grafem 2) Tabulkou x -2 -1 0 1 2 y -3 -1 1 3 5

Příklady Je dána funkce f: y=2 x-1 ; x R. Rozhodněte, která z následujících dvojic [x; y] patří funkci f. [0; 1] [0; -1] Ne Ano [3/2; -2] Ne [0, 25; -1/2] Ano [-1/4; -1, 5] Ano