Rozcvika Uri typ funkce Dostupn z Metodickho portlu

Rozcvička Urči typ funkce: Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Rozcvička Doplň chybějící souřadnici: Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

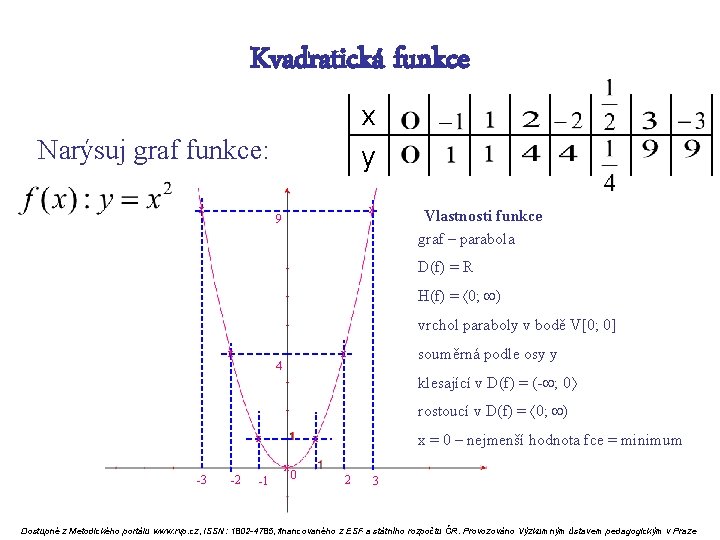
Kvadratická funkce x y Narýsuj graf funkce: x x 9 Vlastnosti funkce graf – parabola D(f) = R H(f) = 0; vrchol paraboly v bodě V[0; 0] x souměrná podle osy y x 4 klesající v D(f) = (- ; 0 rostoucí v D(f) = 0; x -3 -2 x -1 x = 0 – nejmenší hodnota fce = minimum x 0 2 3 Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

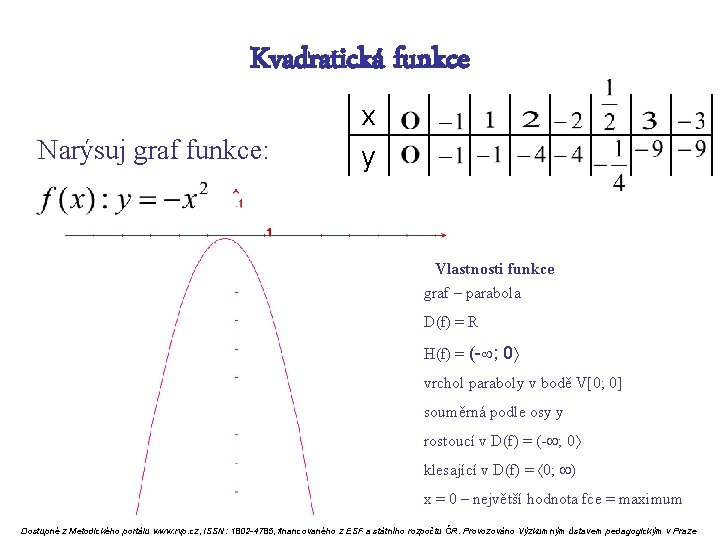
Kvadratická funkce Narýsuj graf funkce: x y Vlastnosti funkce graf – parabola D(f) = R H(f) = (- ; 0 vrchol paraboly v bodě V[0; 0] souměrná podle osy y rostoucí v D(f) = (- ; 0 klesající v D(f) = 0; x = 0 – největší hodnota fce = maximum Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

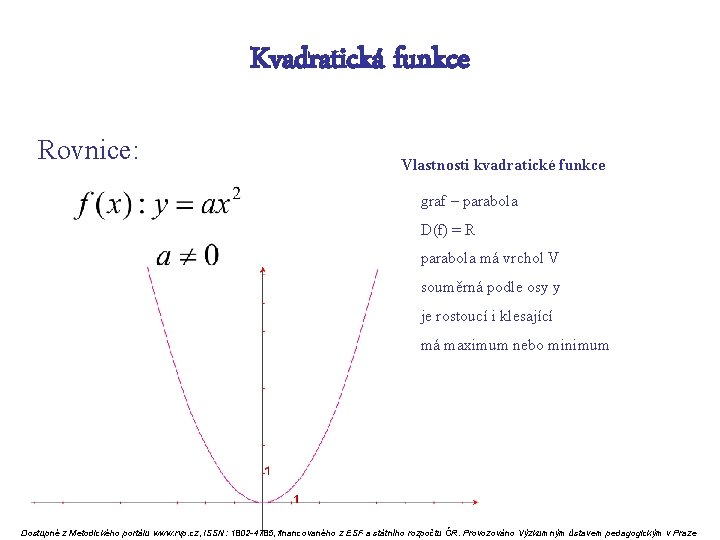
Kvadratická funkce Rovnice: Vlastnosti kvadratické funkce graf – parabola D(f) = R parabola má vrchol V souměrná podle osy y je rostoucí i klesající má maximum nebo minimum Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

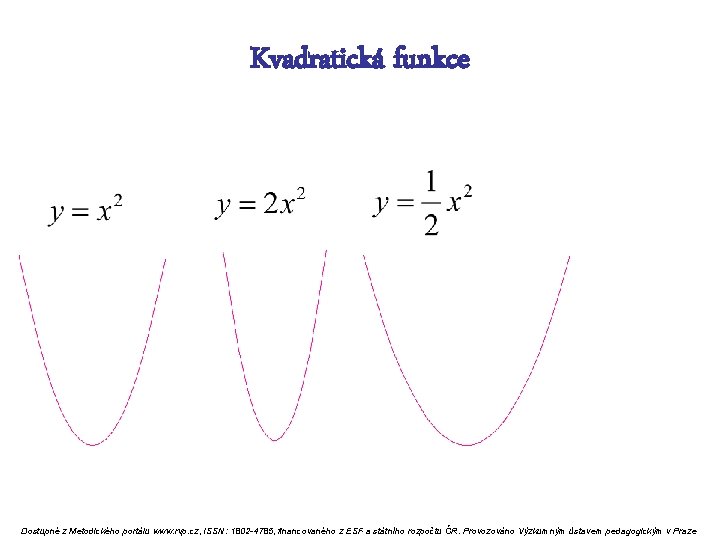
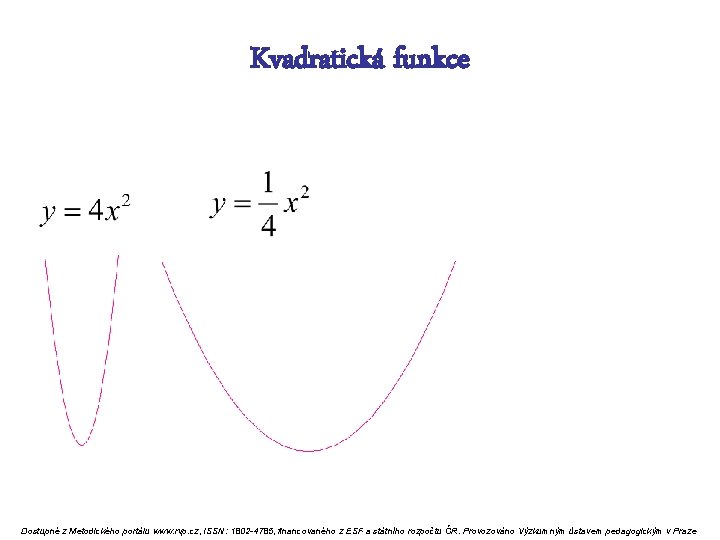
Kvadratická funkce v závislosti na a je-li a>0, potom má kvadratická funkce vždy minimum Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

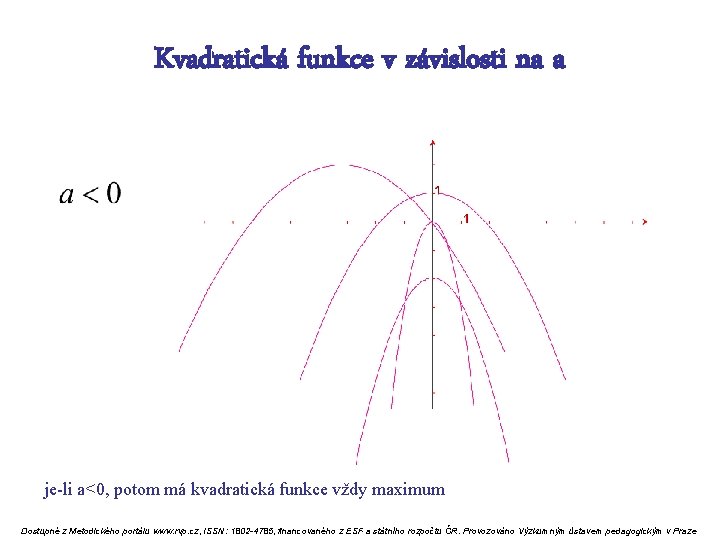
Kvadratická funkce v závislosti na a je-li a<0, potom má kvadratická funkce vždy maximum Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Kvadratická funkce Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Kvadratická funkce Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Kvadratická funkce Narýsuj graf funkce f: y = - x 2 a) urči největší hodnotu této funkce b) jaká je hodnota této funkce pro x = 2 c) pro která x je hodnota této funkce rovna (-1) d) v jakém intervalu je tato funkce rostoucí e) pro která x je hodnota této funkce největší Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

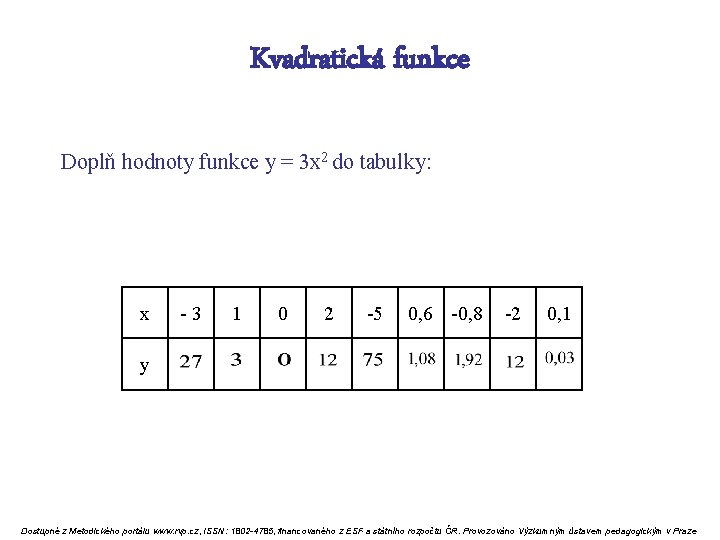
Kvadratická funkce Doplň hodnoty funkce y = 3 x 2 do tabulky: x - 3 1 0 2 -5 0, 6 -0, 8 -2 0, 1 y Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Kvadratická funkce Doplň na místa otazníků taková čísla, aby uvedené body patřily do grafu kvadratické funkce: A[ 1 ; ? ] B[ 2 ; ? ] C[ -1 ; ? ] D[ 0, 1 ; ? ] E[ ? ; 8 ] bod E nepatří do dané fce Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Kvadratická funkce Doplň na místa otazníků taková čísla, aby uvedené body patřily do grafu kvadratické funkce: A[ 1 ; ? ] B[ 2 ; ? ] C[ -1 ; ? ] D[ 0, 1 ; ? ] E[ ? ; 8 ] Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Kvadratická funkce Doplň na místa otazníků taková čísla, aby uvedené body patřily do grafu kvadratické funkce: A[ 1 ; ? ] B[ 2 ; ? ] C[ -1 ; ? ] D[ 0, 1 ; ? ] E[ ? ; 8 ] Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Kvadratická funkce Doplň na místa otazníků taková čísla, aby uvedené body patřily do grafu kvadratické funkce: A[ 1 ; ? ] B[ 2 ; ? ] C[ -1 ; ? ] D[ 0, 1 ; ? ] E[ ? ; 8 ] Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

Kvadratická funkce Na grafu kvadratické funkce y = ax 2 leží bod a) A[ -3 ; -18 ] b) B[ -2 ; -10 ] c) C[ 2 ; 2 ] Urči čemu se rovná a. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

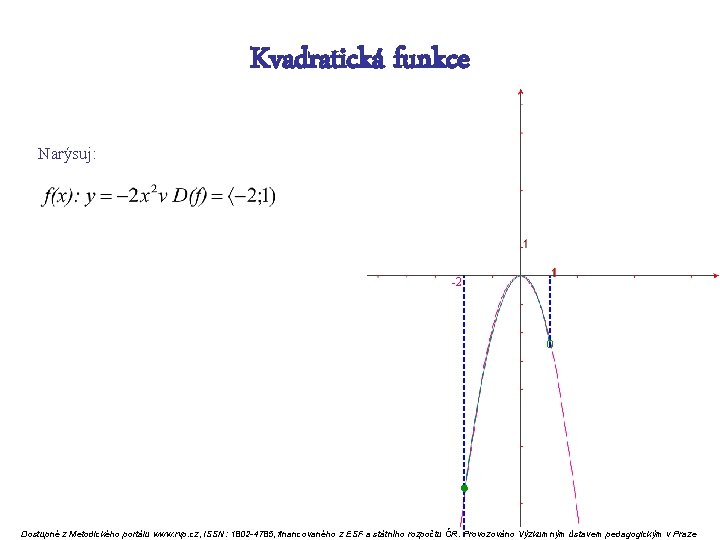
Kvadratická funkce Narýsuj: -2 o Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze

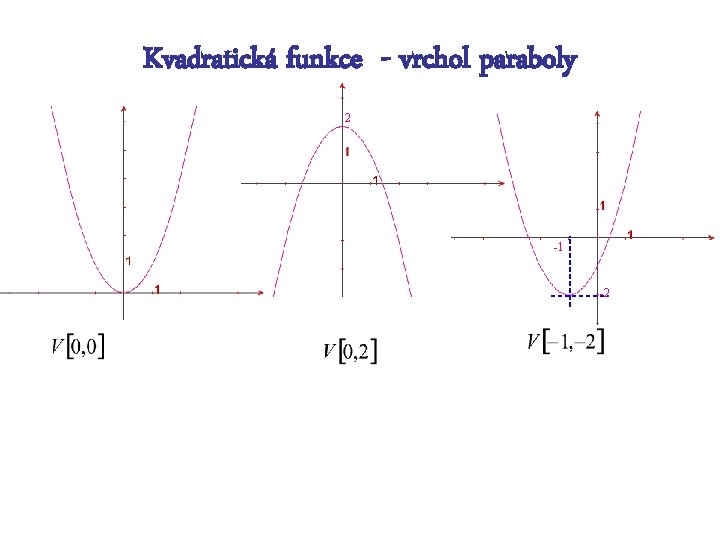
Kvadratická funkce - vrchol paraboly 2 -1 -2

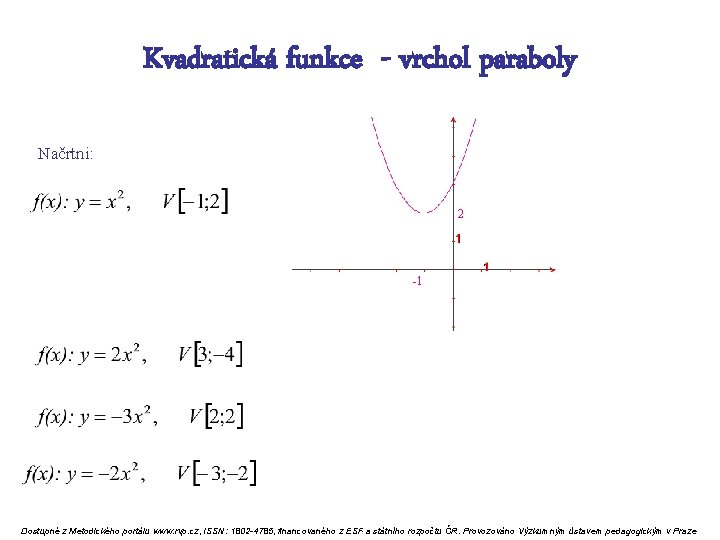
Kvadratická funkce - vrchol paraboly Načrtni: 2 -1 Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze