Funkce Linern funkce Dostupn z Metodickho portlu www

Funkce Lineární funkce Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Lineární funkce Definice Každá funkce y = ax + b, kde a, b jsou libovolná reálná čísla a definičním oborem je množina všech reálných čísel, se nazývá lineární funkce. Grafem lineární funkce je přímka.

Úkol y Sestrojte graf lineární funkce y = 3 x – 2. 5 4 3 x y = 3 x – 2 2 1 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 1 2 A[0; – 2] 3 4 1 1 2 4 x Všímej si souřadnic průsečíku grafu s osou y. Označíme jej bodem A, platí A[0; -2], y-nová souřadnice bodu A je rovna konstantě b v rovnici funkce.

Příklady 1. Kterému číslu je rovna konstanta b v zadání lineární funkce y = 2 x + b, jestliže graf této funkce protíná osu y v bodě o souřadnicích [0; 5]? b=5 y = 2 x + 5 2. Určete, jaké souřadnice bude mít bod, ve kterém protíná graf lineární funkce y = 3 x – 5 osu y. [0; – 5] 3. Zapište lineární funkci, jestliže víte, že platí: a = 5, b = 0. Jaké souřadnice má bod, ve kterém graf této funkce protíná osu y? y = 5 x bodem [0; 0]

Závěr • Graf lineární funkce y = ax + b protíná osu y v bodě o souřadnicích [0; b]. • Graf lineární funkce y = ax (b = 0) prochází počátkem soustavy souřadnic [0; 0].

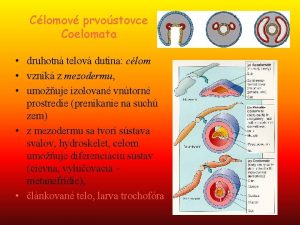
y Lineární funkce y = 3 x – 2 C[-2; 4] 5 4 3 B[2; 4] 2 1 -4 -3 0 -2 -1 -1 -2 -3 -4 -5 1 2 3 4 A[0; – 2] x Funkce je rostoucí, právě když pro každé dvě hodnoty x 1, x 2 z jejího definičního oboru platí: jestliže x 1 < x 2, pak y 1 < y 2. x 0 2 y = 3 x – 2 -2 4 Funkce je klesající, právě když pro každé dvě hodnoty x 1, x 2 z jejího definičního oboru platí: jestliže x 1 < x 2, pak y 1 > y 2. x 0 – 2 y = – 3 x – 2 -2 4 y = – 3 x – 2 Pozoruj číslo a v rovnici. Co vidíš?

Lineární funkce y = ax + b je rostoucí, jestliže a > 0. Uveď příklady rostoucí funkce. Např. : y = x – 4; y = 0, 3 x + 0, 1; y = 1, 4 x – 5; Lineární funkce y = ax + b je klesající, jestliže a < 0. Uveď příklady klesající funkce. Např. : y = – 2 x – 5; y = – x + 1; y = – 0, 4 x – 5;

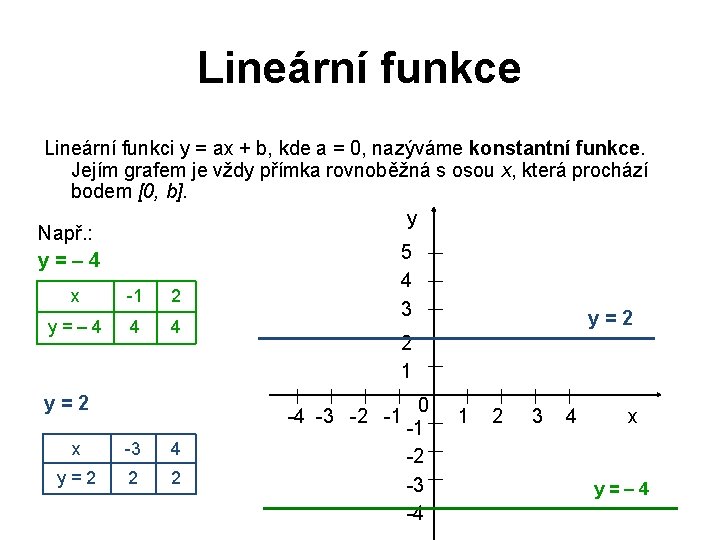
Lineární funkce Lineární funkci y = ax + b, kde a = 0, nazýváme konstantní funkce. Jejím grafem je vždy přímka rovnoběžná s osou x, která prochází bodem [0, b]. y Např. : 5 y=– 4 4 x -1 2 3 y=2 y = – 4 4 4 y=2 2 1 -4 -3 -2 -1 x -3 4 y = 2 2 2 0 -1 -2 -3 -4 1 2 3 4 x y=– 4

Příklady 1. Rozhodněte, která z daných funkcí je lineární. Df = R. a) y = 2 x + 1 b) y = x 2 – 5 c) y = 0, 5 – 2 x d) e) f) 2. Určete průsečíky grafů daných funkcí s osou y: a) y = – x + 3 b) y = 7 x + 15 c) y = 0, 5 x - 0, 6 3. Rozhodněte, zda je daná funkce rostoucí nebo klesající: a) y = – 5 x b) y = 2 x – 4 c) y = – 0, 3 x + 0, 5 d) y = – 8 e) y = 1 – x Řešení: a), c), e), f) a) [0; 3] a) [0; 15] a) [0; - 0, 6] a) klesající b) rostoucí c) klesající d) konstantní e) klesající

Příklady 4. Sestrojte grafy lineárních funkcí. Df = R. a) y = 2 x + 1 b) y = 2 x c) y = 2 x – 3 d) y = 2 x + 3 Řešení: 5. Sestrojte grafy lineárních funkcí. Df = R. a) y = – x + 3 b) y = x + 3 c) y = 6 x – 2 d) y = – 6 x – 2 Řešení: 6. a) Zapište libovolnou rostoucí lineární funkci a sestrojte její graf. b) Zapište libovolnou klesající lineární funkci a sestrojte její graf.

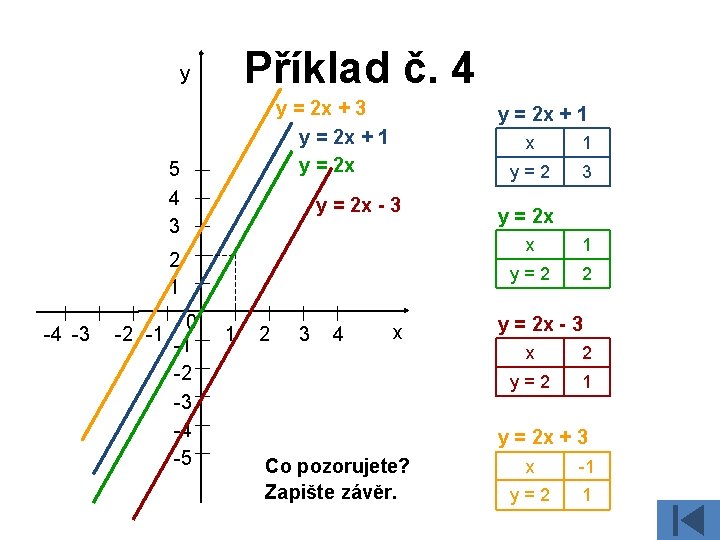
Příklad č. 4 y y = 2 x + 3 y = 2 x + 1 y = 2 x 5 4 3 y = 2 x + 1 y = 2 x - 3 2 1 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 1 2 3 4 x x 1 y = 2 3 y = 2 x x 1 y = 2 2 y = 2 x - 3 x 2 y = 2 1 y = 2 x + 3 Co pozorujete? Zapište závěr. x -1 y = 2 1

y y = – x + 3 Příklad č. 5 y = x + 3 5 4 3 -2 -1 y = 6 x – 2 x 1 y = 2 2 y = x + 3 2 1 -4 -3 y = – x + 3 0 x 1 2 3 4 -1 -2 -3 y = – 6 x – 2 -4 -5 Co pozorujete? Zapište závěr. x -2 y = 2 1 y = 6 x – 2 x 1 y = 2 4 y = – 6 x – 2 x -1 y = 2 4

Příklady z praxe 1. V balonu je 1, 8 kg tekutého propanu. Plynovým hořákem se spotřebuje každou hodinu 0, 2 kg propanu. Jaké množství m propanu bude v balonu za t hodin letu? Sestrojte graf a určete z něho: a) Kolik kg propanu bude v balonu za 3 h; 5 h; 6, 5 h? b) Za jakou dobu se zmenší zásoba propanu o 0, 6 kg; 1, 5 kg? 2. Sestrojte grafy funkcí vyjadřujících závislost velikosti proudu I na napětí U podle Ohmova zákona pro odpory: R 1 = 10 , R 2 = 25 , R 3 = 50 . 3. Na natření 10 metrů plotu se spotřebuje 4, 5 kg barvy. Natěrač má zásobu 20 kg barvy. Napište rovnici popisující závislost množství zásoby barvy (y kg) na délce natřeného plotu (x m). Určete podmínku pro x.

Příklady z praxe 4. Napište rovnici funkce vyjadřující závislost počtu vyrobených součástek n na čase t (v hodinách) na pravidelně pracujícím automatu, který vyrobí za 8 hodin vždy 120 součástek. 5. Silnice stejnoměrně klesá. Určete graficky výšku bodu, který je vzdálen od místa A 15 km, má-li bod vzdálený od místa A 5 km výšku 150 m a bod vzdálený od místa A 9 km výšku 120 metrů. 6. Cisterna na naftu se má naplnit na 55 m 3. Čerpadlo dodá do cisterny 3, 5 m 3 nafty za minutu. Před začátkem činnosti čerpadla bylo již 6 m 3 nafty. Určete graficky, za jak dlouho se cisterna naplní. 7. Auto a motorka vyjíždějí z místa B po stejné trase tak, že nejprve vyjede auto průměrnou rychlostí 50 km/h a za dvě hodiny za ním motorka průměrnou rychlostí 70 km/h. Určete graficky, kdy a v jaké vzdálenosti od výchozího místa motorka auto dohoní.

Příklady z praxe - řešení Řešení: 1) m = - 0, 2 t + 1, 8; m 3 = 1, 2 kg; m 5 = 0, 8 kg; m 6, 5 = 0, 5 kg; 3 h, 5 h, 7, 5 h 2) I = 0, 1 U; I = 0, 04 U; I = 0, 02 U 3) y = - 0, 45 x + 20; 0 m ≤ x ≤ 400/9 m 4) n = 15 t 5) 75 m 6) y = 3, 5 x + 6 7) y 1 = 50 x + 100; y 2 = 70 x; 5 h; 350 km