CLCULO III AULA 3 Os Vetores Tangente Unitrio

CÁLCULO III AULA 3 – Os Vetores Tangente Unitário, Normal Principal e Curvatura

CÁLCULO III Conteúdo Programático 1. Vetor tangente 2. Reta tangente 3. Vetor tangente unitário 4. Vetor Normal principal 5. Curvatura Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

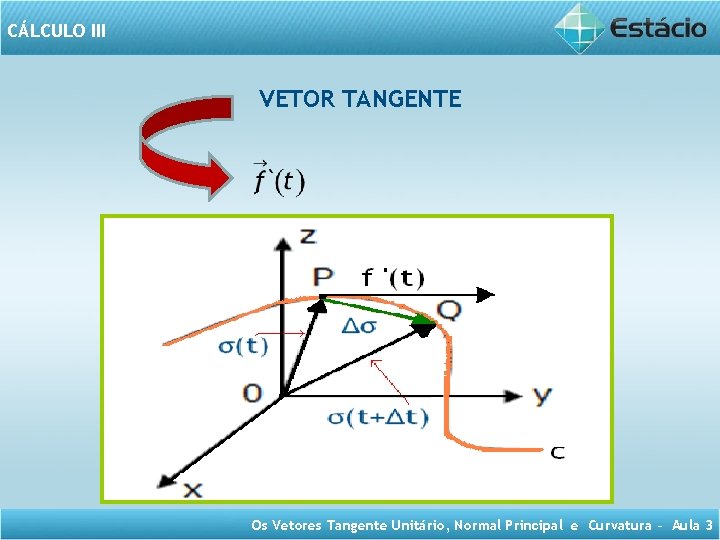
CÁLCULO III VETOR TANGENTE Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLOS 1. Determinar o vetor tangente da seguinte função, no ponto indicado. Inicialmente devemos identificar o valor do parâmetro t que satisfaz a curva. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Agora podemos calcular a derivada da f(t) no ponto t 0 = -1. 2. Determinar o vetor tangente da seguinte função, no ponto indicado. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Inicialmente devemos identificar o valor do parâmetro t que satisfaz a curva. Agora podemos calcular a derivada da g(t) no ponto t 0 = 1. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III 3. Determinar o vetor tangente da seguinte função, no ponto indicado. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Agora podemos calcular a derivada da f(t) no ponto t 0 = π. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III RETA TANGENTE Seja C uma curva representada por Vamos considerar P(x, y, z) um ponto de C e to um parâmetro. Conforme estudamos na aula 1 o vetor curva no ponto P. é tangente à Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III O vetor σ’(to ) determina a reta tangente em cada ponto da curva. Considerando σ(to ) = P e σ’(to ) = o vetor tangente a curva em P. A reta passa por um ponto P com direção Tem como equação r(t) = σ(to ) + t. σ’(to ) , t é um parâmetro real. Podemos escrever: Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO 1 Determinar a reta tangente da seguinte função, no ponto indicado. Inicialmente devemos identificar o valor do parâmetro t que satisfaz a curva. Vamos considerar t 0 = 1. Derivamos a função vetorial dada. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Esta função nos leva ao vetor diretor ou seja, o vetor v = (3, 2, 1). A reta tangente será: Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III OBSERVAÇÃO P Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO 2 Determinar a reta tangente da seguinte função, no ponto indicado. Para obter o valor de t 0, correspondente ao ponto P, usamos as equações paramétricas da curva. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III A equação da reta tangente será dada por Podemos também escrever Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III VETOR TANGENTE UNITÁRIO Dada a curva C, desejamos encontrar, em cada ponto dessa curva, um vetor tangente à curva, que seja unitário. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III C é uma curva representada por r (t) = (x(t), y(t), z(t)) e vimos que o vetor r’(t) é tangente à curva C. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III DEFINIÇÃO O vetor é chamado de vetor tangente unitário à curva C. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

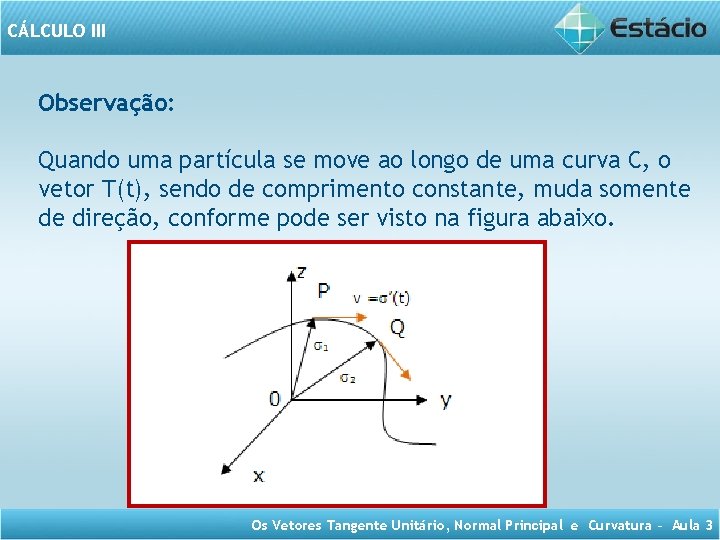
CÁLCULO III Observação: Quando uma partícula se move ao longo de uma curva C, o vetor T(t), sendo de comprimento constante, muda somente de direção, conforme pode ser visto na figura abaixo. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO 1 Encontre o vetor T(t) a curva (t) = ( cos t, sen t), t ≥ 0 Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO 2 Encontre o vetor T(t) a curva (t) = (et + 1, e-t – 1, t) no ponto P(2, 0, 0). Para obter o valor de t 0, correspondente ao ponto P, usamos as equações paramétricas da curva. x(t) = et + 1 → et + 1 = 2 → et = 1 → t = 0 y(t) = e-t - 1 → e-t - 1 = 0 → e-t = 1 → t = 0 z(t) = t→ t = 0 Portanto t 0 = 0. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III (t) = (et + 1, e-t – 1, t) ’(t) = (et, -e-t, 1) ’(0) = (e 0, -e 0, 1) = (1, -1, 1) T 0 = 0 Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Portanto, Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III VETOR NORMAL PRINCIPAL. . . quando uma partícula se move ao longo de uma curva C, o vetor T(t), sendo de comprimento constante, muda somente de direção. A variação desta direção é medida pela derivada. Podemos concluir que T(t) é perpendicular a T’(t). Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

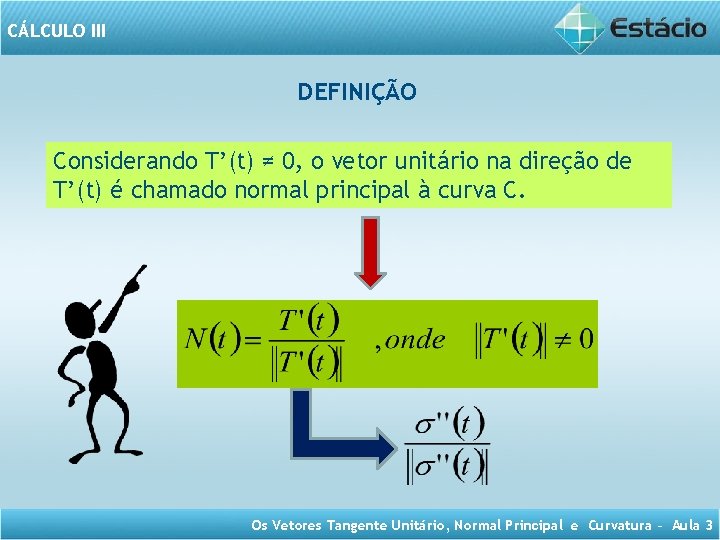
CÁLCULO III DEFINIÇÃO Considerando T’(t) ≠ 0, o vetor unitário na direção de T’(t) é chamado normal principal à curva C. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

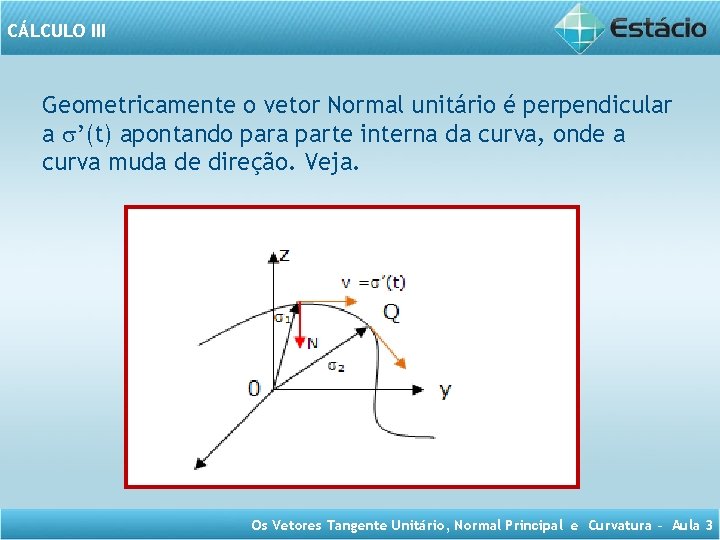
CÁLCULO III Geometricamente o vetor Normal unitário é perpendicular a ’(t) apontando para parte interna da curva, onde a curva muda de direção. Veja. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO 1 Vamos encontrar o vetor N(t) a curva (t) = ( cos t, sen t), t ≥ 0 ’(t) = (-sent, cos t) ’’(t)= (-cos t, -sent) Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO 2 Vamos escrever o vetor normal principal da curva Calculando as derivadas: Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Agora precisamos escrever o vetor normal principal no ponto dado inicialmente, isto é, precisamos determinar N(t 0). Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Determinando t 0: Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III APLICAÇÕES ØComponentes tangencial e normal da aceleração No teorema abaixo veremos que o vetor aceleração é formado pela soma de dois vetores. ØTeorema Considere uma partícula se movendo com vetor posição σ(t). Se v(t) = ||σ’(t)||≠ 0 é a velocidade da partícula , então o vetor aceleração A(t) é dado pelo modelo A(t) = v’(t). T(t) + v(t). T’(t) Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Considerando: A(t) = v’(t). T(t) + v(t). T’(t) Substituindo Podemos escrever Agora temos A(t) = v’(t). T(t) + v(t). ||T’(t)||. N(t) Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III OBSERVAÇÃO SOBRE O TEOREMA O teorema apresentado mostra através do modelo abaixo o vetor aceleração A(t) está sempre no plano definido pelos vetores T(t) e N(t). A(t) = v’(t). T(t) + v(t). ||T’(t)||. N(t) ØT(t) é chamado de componente tangencial da aceleração Notação: A T ØN(t) é chamado de componente normal da aceleração Notação: A N Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO 1 Uma partícula se move ao longo da involuta de equações paramétricas Vamos determinar as componentes tangencial e normal da aceleração. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Vamos recordar algumas definições da aula 2. Vetor velocidade → Velocidade escalar → v(t) = ||σ’(t)|| = ||V(t)|| Vetor aceleração → Vetor velocidade → Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Vetor aceleração Velocidade escalar → v(t) = ||σ’(t)|| = ||V(t)|| Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Componente Tangencial Componente Normal Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO 2 Uma partícula se move ao longo da curva C dada por Determinar: a) Os vetores velocidade e aceleração; b) A velocidade escalar; c) As componentes tangencial e normal da aceleração. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III RESPOSTA a) Os vetores velocidade e aceleração; b) A velocidade escalar; Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III c) As componentes tangencial e normal da aceleração. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III CURVATURA Definição A curvatura de uma curva é a taxa de variação de sua direção, ou seja, a velocidade com que a tangente à curva muda de direção por unidade de comprimento. A expressão acima nos diz que a curvatura é a taxa de variação do vetor tangente unitário em relação ao comprimento de arco. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Cálculo da curvatura Exemplo 1 Determine a curvatura da circunferência de raio a e centro na origem. A parametrização de tal curva será: ( ) = ( a cos , a sen ), 0 ≤ ≤ 2 Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III RESOLUÇÃO ( ) = ( a cos , a sen ), 0 ≤ ≤ 2 ’( ) = (-a sen , a cos ) Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III TEOREMA Se uma partícula em movimento possui vetor velocidade V(t), velocidade escalar v(t), vetor aceleração a(t) e curvatura k(t), então Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III RAIO DE CURVATURA DA TRAJETÓRIA EM UM DADO PONTO P Seja C uma curva e P um ponto em C tal que k(t) existe e k(t) ≠ 0. O inverso da curvatura (k(t) é o raio de curvatura. Vamos chamá-lo de ρ(t) = 1/k(t) O círculo passando por P de raio ρ(t) e cujo centro está na semi-reta normal que contém N(t) é chamando de círculo de curvatura ou círculo osculador. Ele é tangente a C em P. Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III EXEMPLO Determinar o raio de curvatura da parábola r(t) = (t, t 2). A curvatura da parábola é dada por Considerando r(t) na origem, t = 0. Assim, o raio de curvatura é ρ(t) = 1/k(t) → ρ(0) = 1/k(0) = 1/2 Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3

CÁLCULO III RESUMINDO 1. Vetor tangente 2. Reta tangente 3. Vetor tangente unitário 4. Normal principal 5. Curvatura Os Vetores Tangente Unitário, Normal Principal e Curvatura – Aula 3