19112009 2 Trigonometria O significado da palavra trigonometria

19/11/2009

2 Trigonometria O significado da palavra trigonometria, vem do grego e resulta da conjunção de três palavras: Tri – três Gonos – ângulo Metrein - medir Trigonometria significa, o estudo das medidas dos triângulos.

3

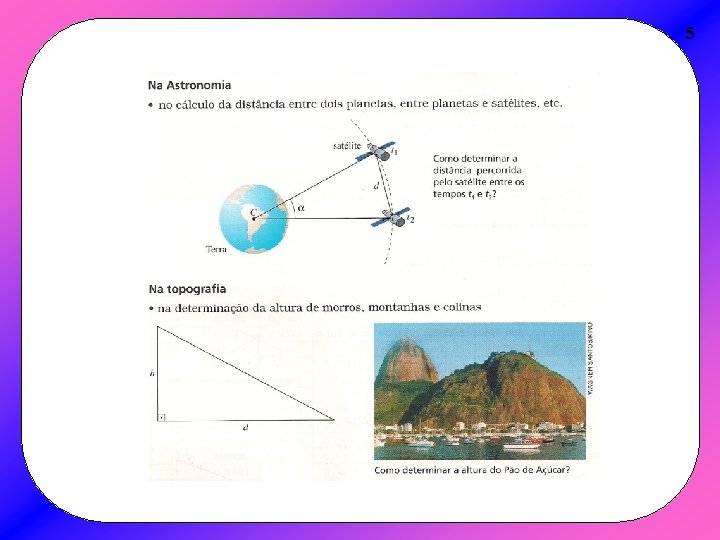
4 Algumas aplicações da Trigonometria

5

6

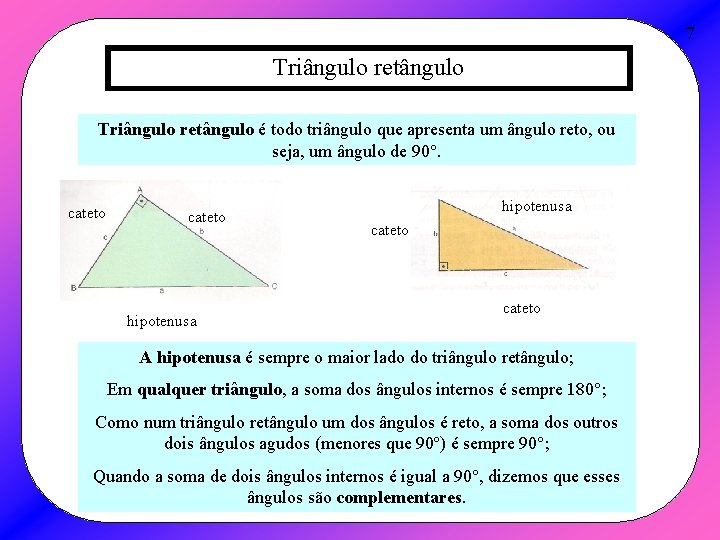
7 Triângulo retângulo é todo triângulo que apresenta um ângulo reto, ou seja, um ângulo de 90°. cateto hipotenusa cateto A hipotenusa é sempre o maior lado do triângulo retângulo; Em qualquer triângulo, a soma dos ângulos internos é sempre 180°; Como num triângulo retângulo um dos ângulos é reto, a soma dos outros dois ângulos agudos (menores que 90º) é sempre 90°; Quando a soma de dois ângulos internos é igual a 90°, dizemos que esses ângulos são complementares.

8 Teorema de Pitágoras Em todo triângulo retângulo, o quadrado da medida da hipotenusa é igual a soma dos quadrados das medidas dos catetos. a=5 b=3 c=4

9 Aplicação do Teorema de Pitágoras

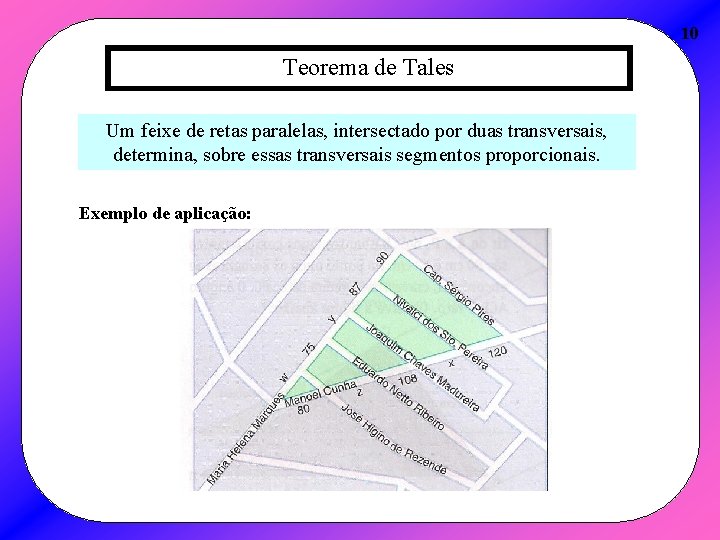
10 Teorema de Tales Um feixe de retas paralelas, intersectado por duas transversais, determina, sobre essas transversais segmentos proporcionais. Exemplo de aplicação:

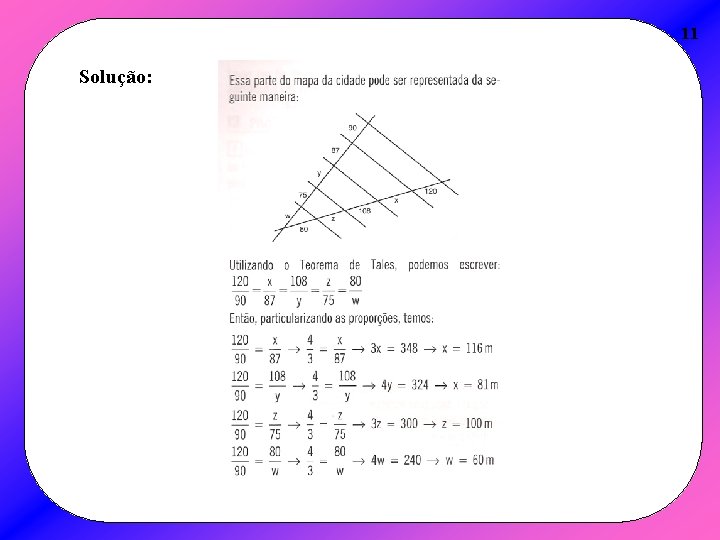
11 Solução:

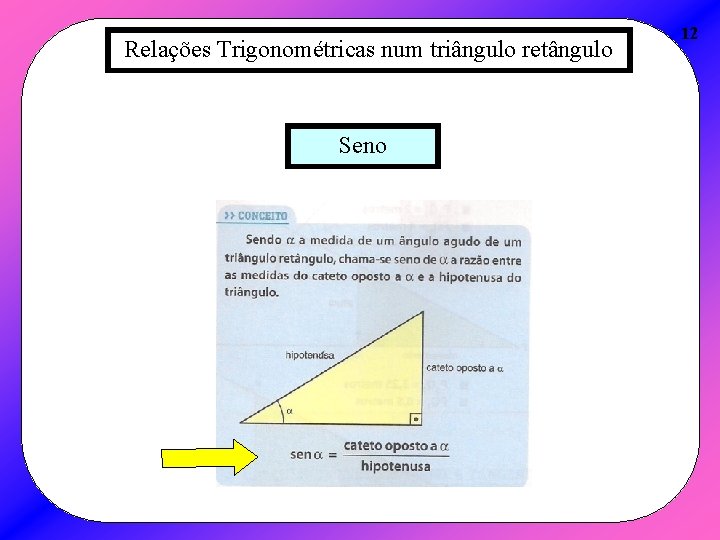
Relações Trigonométricas num triângulo retângulo Seno 12

13 Exemplo de aplicação:

14 Cosseno

15 Exemplo de aplicação:

16 Tangente

17 Exemplo de aplicação:

Cálculo de seno, cosseno e tangente dos ângulos notáveis Seno, cosseno e tangente de 30° e 60º 2 18

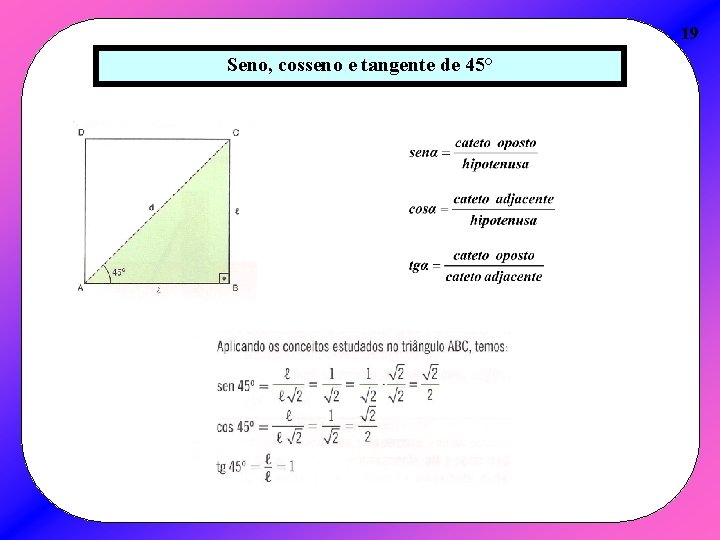
19 Seno, cosseno e tangente de 45°

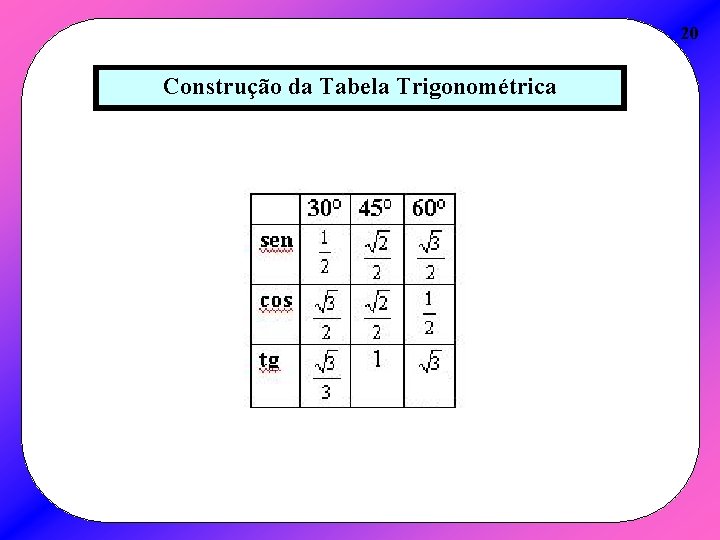
20 Construção da Tabela Trigonométrica

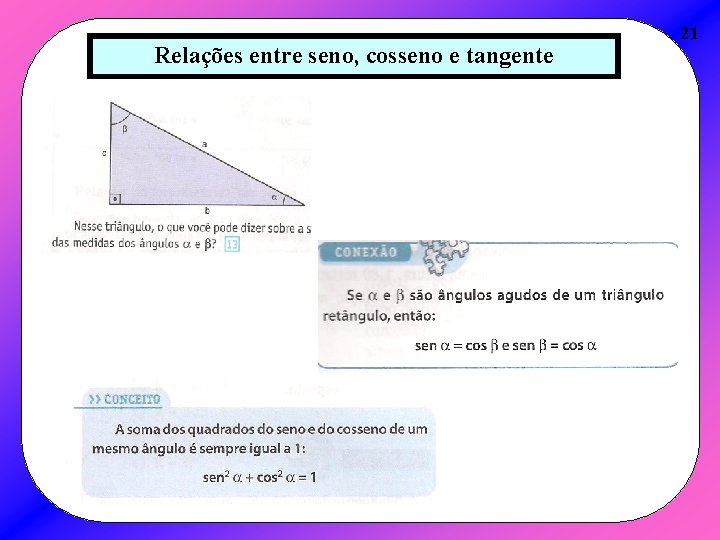
Relações entre seno, cosseno e tangente 21

22

23 Observe a situação a seguir: Um fio elétrico será instalado entre um poste P e uma casa, separados por um lago em um terreno plano. Como calcular o comprimento do fio necessário para a instalação? Pela necessidade de solucionar problemas relacionados a triângulos que não são retângulos, se desenvolveram formas de trabalhar com senos e cossenos de ângulos obtusos ( maiores que 90°).

24 Teorema ou Lei dos Senos A lei dos senos pode ser utilizada em qualquer triângulo. No caso de triângulos retângulos, basta considerar sen 90° = 1.

25 Aplicação da Lei dos Senos A Lei dos Senos é geralmente usada, quando são conhecidos 2 ângulos internos e a medida do cateto oposto a um desses ângulos.

26 Teorema ou Lei dos Cossenos A Lei dos Cossenos é geralmente usada, quando são conhecidas as medidas de dois lados e o ângulo formado por eles.

27 Exemplo:

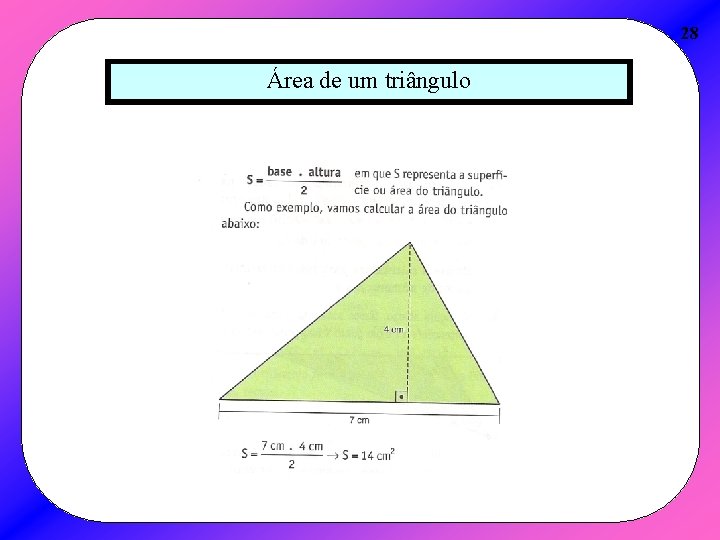
28 Área de um triângulo

29 Existem problemas em que se deseja calcular a área de um triângulo e não são conhecidas as medidas da base e altura. Nesses casos, a área pode ser calculada de duas maneiras diferentes: 1ª maneira: Área de um triângulo em função da medidas de dois lados e do ângulo compreendido entre eles.

30 2ª maneira: Fórmula de Heron

31

32 ARCOS E NGULOS

33 NGULO CENTRAL Todo ângulo central possui um arco correspondente, e reciprocamente, a todo arco corresponde um ângulo central. A medida de um arco é entendida como a medida do seu ângulo central. Para medir um arco, usamos o grau ou o radiano. O comprimento de um arco é a sua medida linear e é expresso em centímetros, metros. . . IMPORTANTE Os arcos AB e A’B’ têm a mesma “abertura”, ou seja, a mesma medida (mesmo ângulo), mas possuem comprimentos diferentes.

34 MEDIDA DE ARCOS: O GRAU O grau é definido, dividindo-se uma circunferência em 360 partes iguais. Cada uma dessas partes, corresponde a um arco de um grau (1°). Transferidor: usado para medir ângulos.

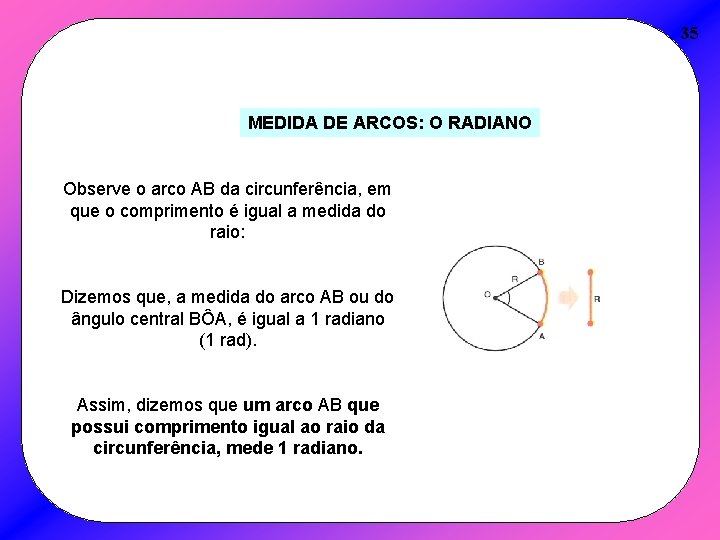
35 MEDIDA DE ARCOS: O RADIANO Observe o arco AB da circunferência, em que o comprimento é igual a medida do raio: Dizemos que, a medida do arco AB ou do ângulo central BÔA, é igual a 1 radiano (1 rad). Assim, dizemos que um arco AB que possui comprimento igual ao raio da circunferência, mede 1 radiano.

36 Qual é o comprimento de uma circunferência? Qual é a medida em radianos de um arco de 360°?

37 Portanto, temos que: Quantos graus mede um arco de 1 radiano?

38 CIRCUNFERÊNCIA TRIGONOMÉTRICA

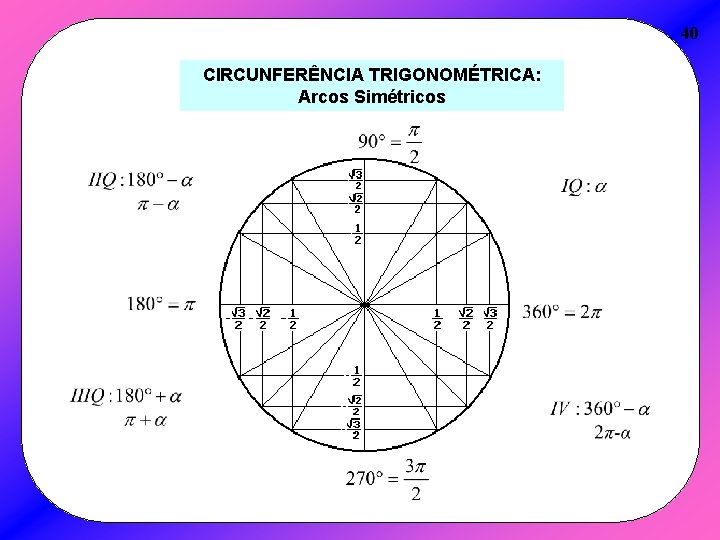
40 CIRCUNFERÊNCIA TRIGONOMÉTRICA: Arcos Simétricos

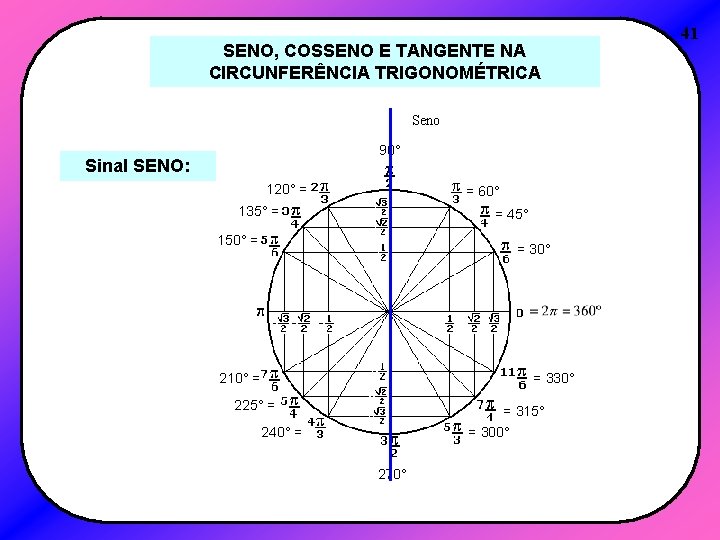
SENO, COSSENO E TANGENTE NA CIRCUNFERÊNCIA TRIGONOMÉTRICA Seno 90° Sinal SENO: 120° = = 60° 135° = = 45° 150° = = 30° 210° = = 330° 225° = = 315° = 300° 240° = 270° 41

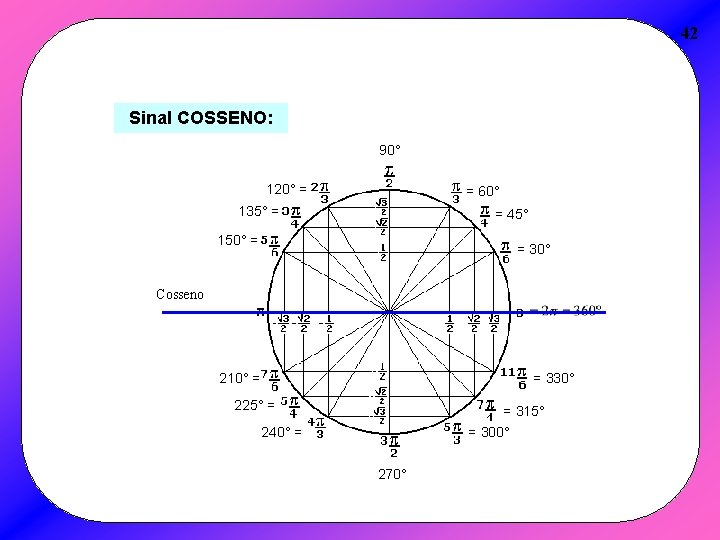
42 Sinal COSSENO: 90° 120° = = 60° 135° = = 45° 150° = = 30° Cosseno 210° = = 330° 225° = = 315° = 300° 240° = 270°

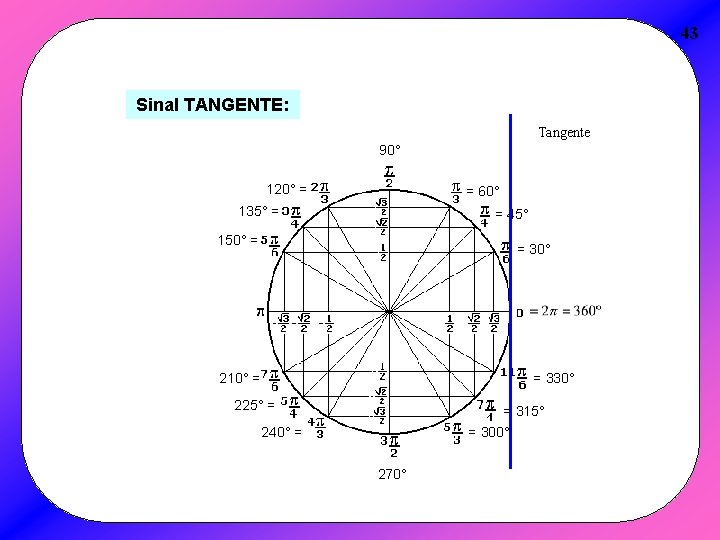
43 Sinal TANGENTE: Tangente 90° 120° = = 60° 135° = = 45° 150° = = 30° 210° = = 330° 225° = = 315° = 300° 240° = 270°

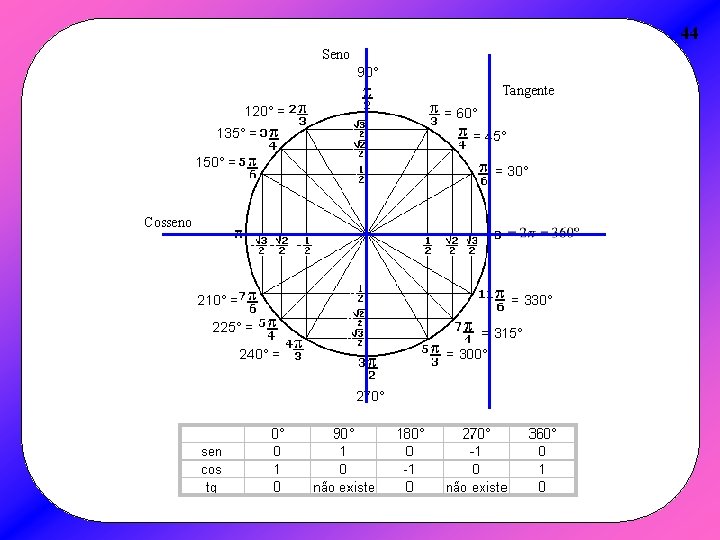
44 Seno 90° Tangente 120° = = 60° 135° = = 45° 150° = = 30° Cosseno 210° = = 330° 225° = = 315° = 300° 240° = 270°

45 DEMAIS RAZÕES TRIGONOMÉTRICAS Secante: o sinal da secante é o mesmo do cosseno Cossecante: o sinal da cossecante é o mesmo do seno Cotangente: o sinal da cotangente é o mesmo da tangente.