CLCULO III AULA 1 FUNES COM VALORES VETORIAIS

CÁLCULO III AULA 1 – FUNÇÕES COM VALORES VETORIAIS

CÁLCULO III Conteúdo Programático 1. Introdução 2. Aplicações 3. Definição 4. Operações com as funções vetoriais 5. Limite e Continuidade 6. Derivada 7. Curvas Parametrizadas 8. Reta Tangente FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III INTRODUÇÃO FUNÇÕES COM VALORES VETORIAIS funções vetoriais de uma variável Função f(t), onde t é uma variável real Função vetorial → domínio é um conjunto de números reais e cuja imagem é um conjunto de vetores FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III APLICAÇÃO ØMovimento de uma partícula no Espaço Podemos associar uma partícula no espaço como sendo um ponto no espaço. Observe que o deslocamento deste ponto em cada instante de tempo t descreverá uma curva. x = x(t), y = y(t) e z = z(t) σ(t) = (x(t), y(t), z(t)), definidos no intervalo I, I , com valores em 3, t I. Exemplo: (t) = (t 2 , cos t, t 3) então x(t) = t 2 , y(t) = cos t e z(t) = t 3 FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III APLICAÇÃO FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III DEFINIÇÃO Função vetorial de uma variável real t é definida num intervalo I, onde para cada t I associamos um vetor do espaço. Notação: Uma função cujo domínio é um conjunto de números reais e cuja imagem é um conjunto de vetores é chamada função vetorial. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Se considerarmos um ponto P(x, y, z) qualquer no espaço, o vetor É chamado vetor posição do ponto P. FUNÇÕES COM VALORES VETORIAIS – AULA 1

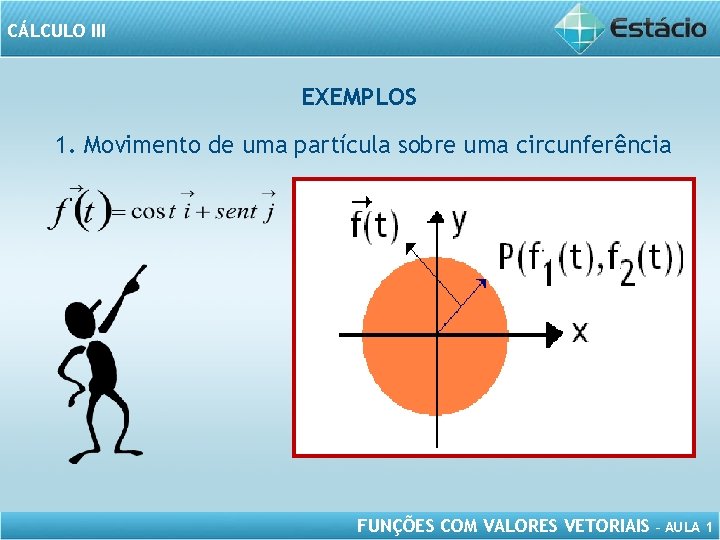
CÁLCULO III EXEMPLOS 1. Movimento de uma partícula sobre uma circunferência FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 2. Função vetorial preço Podemos considerar 3 produtos onde o primeiro tem preço t 2 , o segundo tem preço t + 5 e o terceiro tem preço dado pela soma dos preços das duas primeiras. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III OPERAÇÕES COM FUNÇÕES VETORIAIS FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III LIMITE E CONTINUIDADE Definição: Ou seja, o limite de um vetor f(t) quando t se aproxima de t 1 é definido por: Se os limites individuais existirem FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 1. Considere a função vetorial Veja que o limite da função será determinado do seguinte modo: FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 2. Considere a função vetorial Vamos analisar o valor do limite da função quando t → 2. Podemos usar a regra de L’Hospital para resolver esse limite FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III ØUsando a regra de L’Hospital ØOutro modo de resolver esse limite FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III CONCLUSÃO FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 3. Vamos calcular o FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III CONTINUIDADE Definição: A função vetorial é contínua em t I se, e somente se x(t), y(t) e z(t) são contínuas em t. Segundo o critério de continuidade de uma função, a função será contínua, caso o limite e a função no ponto em estudo existam e sejam iguais, isto é, FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 1. Vamos analisar a continuidade da vetorial dada, no ponto indicado. Veja: Portanto a função é contínua no ponto t = 0. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 2. Vamos analisar a continuidade da vetorial dada, no ponto t 1 = 0. Veja que o e Portanto a função dada não é contínua no ponto indicado. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III DERIVADA Definição: A derivada da função vetorial , t I, é a função vetorial denotada por e definida por: Para todo t, tal que o limite existe. Se a derivada da função existe em todos os pontos do intervalo I, então podemos dizer que a função é derivável em I. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Considere a função vetorial Ela é derivável em um ponto t se, e somente se, as três funções escalares São deriváveis em t. Logo podemos escrever FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS Vamos determinar a derivada das seguintes funções vetoriais: FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS FUNÇÕES COM VALORES VETORIAIS – AULA 1

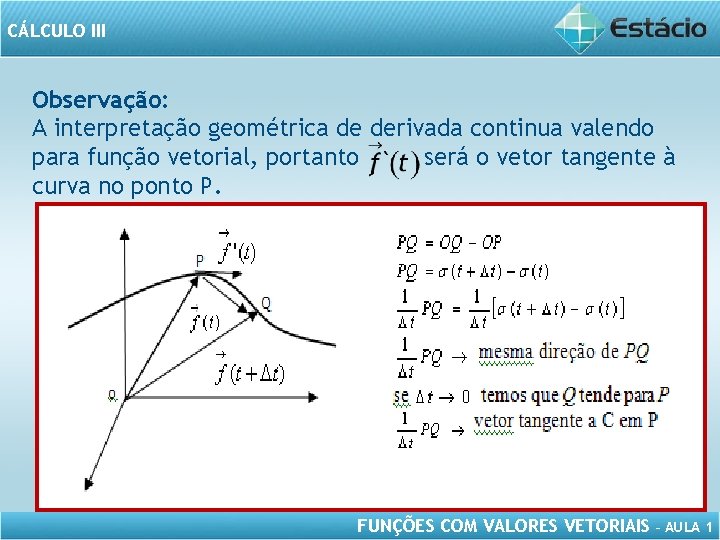
CÁLCULO III Observação: A interpretação geométrica de derivada continua valendo para função vetorial, portanto será o vetor tangente à curva no ponto P. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLO Determinar o vetor tangente da seguinte função, no ponto indicado. Inicialmente devemos identificar o valor do parâmetro t que satisfaz a curva. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Agora calculamos a derivada. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III INTERPRETAÇÃO FÍSICA DA DERIVADA Considere uma partícula em movimento no espaço. Vamos supor que no tempo t, representa o vetor posição da partícula. A medida que t varia, a extremidade livre do vetor descreve a trajetória C da partícula. ØQuando é derivável, a velocidade instantânea da partícula é dada por ØQuando é derivável, a aceleração da partícula é dada por FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III CURVAS PARAMETRIZADAS Foi visto anteriormente que um ponto P do vetor descreverá uma curva C em 3 quando for contínua para todo t no intervalo I. Portanto definimos a equação = (x(t), y(t), z(t)) como a parametrização da curva C e as componentes x = x(t) y = y(t) z = z(t) são chamadas de equações paramétricas da curva C e t é chamado parâmetro. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Observação: Chamamos CURVA o conjunto de todos os pontos (x, y, z) determinados por estas equações. Exemplos 1. A equação vetorial Representa uma reta, cujas equações paramétricas são x(t) = t y(t) = t z(t) = t FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III 2. As equações paramétricas x = 2 cost y = 2 sent z = 3 t Representam uma curva no espaço chamada hélice circular. A equação vetorial é representada por FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Parametrização para a hélice circular - curva descrita por um ponto P = (x, y, z) que se move em torno do eixo z mantendo uma distância constante a > 0 desse eixo. Simultaneamente o ponto P se move paralelamente ao eixo z de modo que sua terceira componente é proporcional ao ângulo de rotação com constante de proporcionalidade b≠ 0. Consideramos o início do movimento em P = (0, 0, 0). f(t) = (r cos , r sen , b ) , onde . FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III REPRESENTAÇÃO PARAMÉTRICA DE ALGUMAS CURVAS Parametrização Natural Será a parametrização do tipo f(t) = (t , f( t)). Exemplo A equação da reta y = 6 x + 9 pode ser parametrizada considerando a parametrização natural → f(t) = (t , 6 t+9). FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Podemos também determinar a equação cartesiana correspondente a equação paramétrica de uma curva. Exemplo Seja x = 3 t – 4 e y = 6 – 2 t. Vamos determinar a equação da reta. Procedimento → isolar em uma das equações o parâmetro t e depois substituir na outra, ou isolar o parâmetro t em ambas e igualar as equações. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Veja: Agora vamos substituir (1) em y = 6 – 2 t FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Parametrização de uma reta Equação vetorial da reta → , onde v é o vetor direção, t o parâmetro real e P é um ponto que pertence a reta. = (vx, vy, vz)t + (x 0, y 0, z 0), t =(vxt + x 0, vyt + y 0, vzt + z 0) FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 1. Determinar uma representação paramétrica da reta que passa pelo ponto A(2, 1, -1) na direção do vetor Temos FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 2. Determinar uma representação paramétrica da reta que passa pelo ponto A(2, 0, 1) e B(-1, 3, 0). O vetor v será dado por: v = (-1, 3, 0) - (2, 0, 1) = (-3, 3, -1) Portanto, o vetor r(t) = (2, 0, 1) + t(-3, 3, -1) FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLOS 3. Determinar o vetor direção da reta para a curva Nesse caso verificamos que o ponto P = (0, 0, 0) e a direção v = (1, 1, 1). A reta r será representada por r(t) = (1, 1, 1) t + (0, 0, 0) FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Parametrização da circunferência Seja C a circunferência no plano xy de centro (a, b) e raio r, definimos a parametrização de C como: Circunferência com centro na origem (0, 0): FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III EXEMPLO Vamos obter as equações paramétricas da circunferência x 2 + y 2 – 6 x – 4 y + 4 = 0 no plano z = 3. Completando os quadrados da equação x 2 + y 2 – 6 x + 9 – 4 y + 4 = 9 x 2 – 6 x + 9 + y 2 – 4 y + 4 = 9 (x – 3)2 + (y – 2)2 = 9 x(t) = 3 + 3 cost y(t) = 2 + 3 sent z(t) = 3 0 ≤ t ≤ 2π FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Parametrização da ciclóide curva plana descrita por um ponto P sobre uma circunferência quando esta gira ao longo de uma reta. r (t) = (r ( – sen ), r (1 – cos )) , FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Reta Tangente a trajetória de f(t) no ponto f(t 0 ) Exemplo Calcular a reta tangente para a curva Identificando o valor do parâmetro t que satisfaz a curva observamos que o único valor é t = 1. Derivamos a função vetorial dada. FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III Esta função nos leva ao vetor diretor (vetor tangente a curva), ou seja, o vetor v = (3, 2, 1). A reta tangente será: FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III RESUMINDO FUNÇÕES COM VALORES VETORIAIS – AULA 1

CÁLCULO III FUNÇÕES COM VALORES VETORIAIS – AULA 1