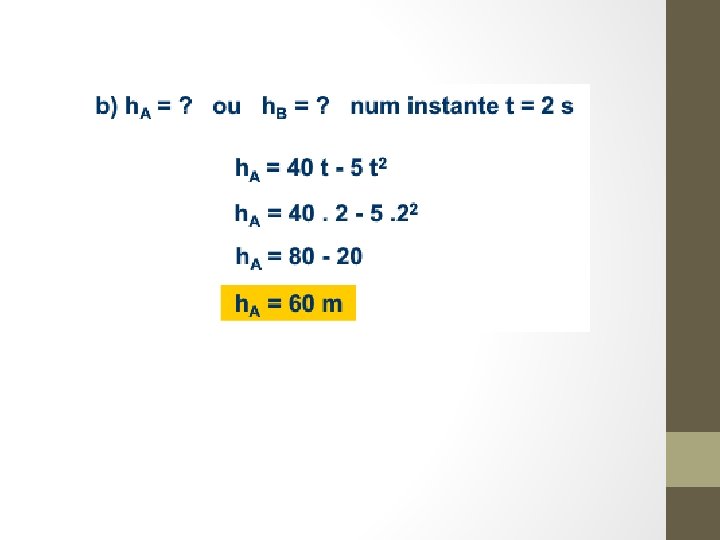FM 05 Vetores Formulrio V constante V varia



















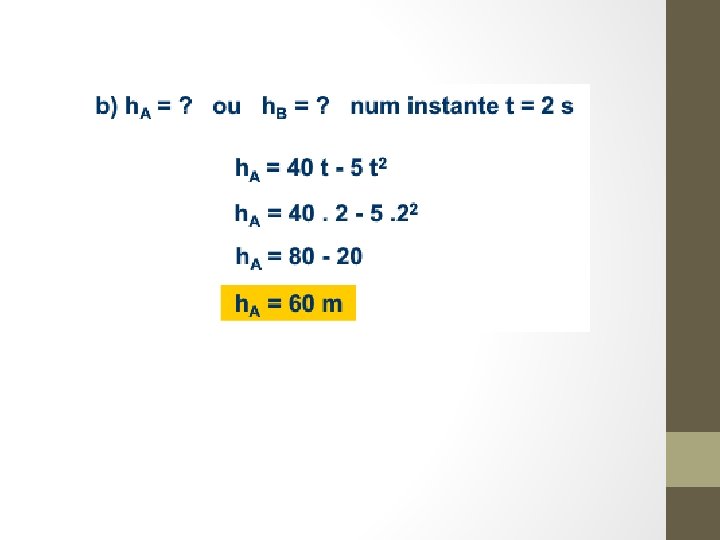
- Slides: 30

FM 05 Vetores

Formulário V = constante V =varia ; a = constante


Grandezas • Grandezas escalares – São aquelas em que apenas com seu valor já esta bem caracterizado. Ex: massa, comprimento etc • Grandezas Vetoriais – São grandezas em que apenas seu modulo não diz muito sobre ela. Além do modulo é necessário indicar também a sua direção e sentido. Ex: Velocidade

Vetores • As grandezas vetoriais precisa de um elemento geométrico para que seja melhor representado. Esse elemento é chamado de VETOR Onde: - O comprimento representa o Modulo - A direção do vetor a representa a direção da grandeza - A seta representa o sentido

Operação com vetores • Podemos mudar os vetores de lugar desde que não se altere seu modulo , sentido ou direção • Uma característica interessante dos vetores é a possibilidade de Soma-los, dando origem a outro vetor. • Veremos a seguir como encontrar o sentido e direção do vetor soma , então vamos nos preocupar apenas com a forma geométrica por enquanto.

Operação com vetores • Com os dois vetores abaixo vamos ver como somamos ? Representamos um vetor com uma flecha em cima Existe três modos e somar vetores mas temporariamente veremos duas: - Regra do Paralelogramo - Regra do Polígono

Regra do paralelogramo É utilizado para soma do vetores dois a dois.

Regra do Polígono • Pode ser usado para dois ou mais. A ideia é fechar um polígono

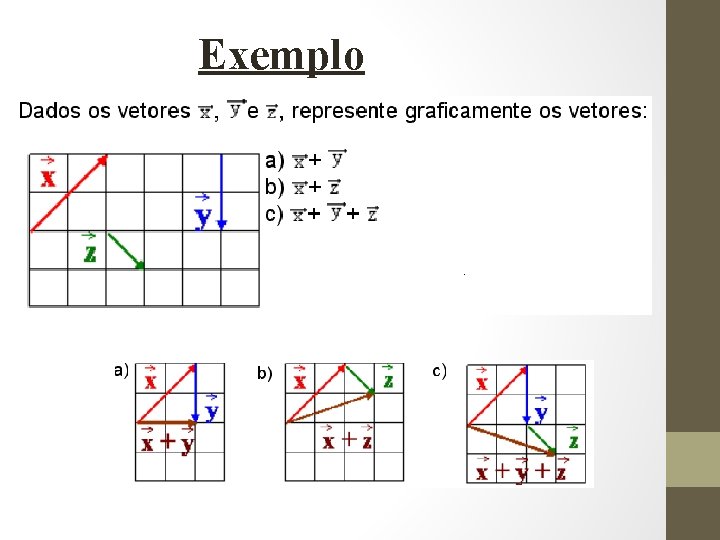
Exemplo

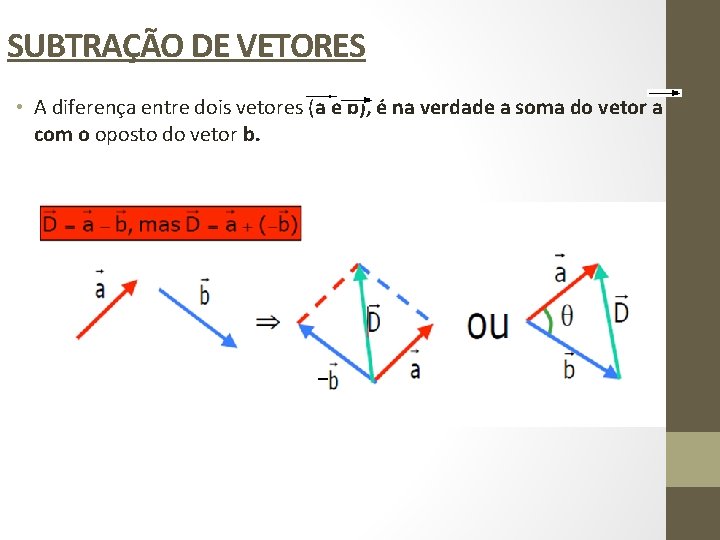
SUBTRAÇÃO DE VETORES • A diferença entre dois vetores (a e b), é na verdade a soma do vetor a com o oposto do vetor b.

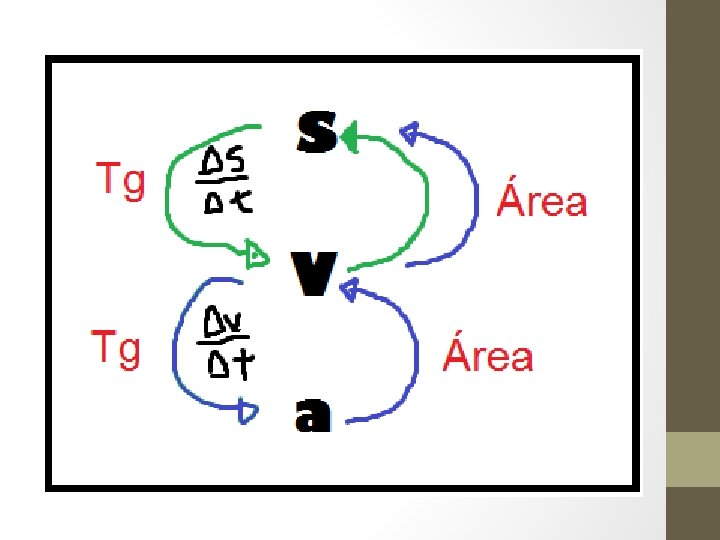
E o modulo ? ? • Para o calculo do modulo teremos que lembrar, para usar como ferramenta, algumas formulas da trigonometria. . . • Lei dos cossenos

Na soma Na subtração

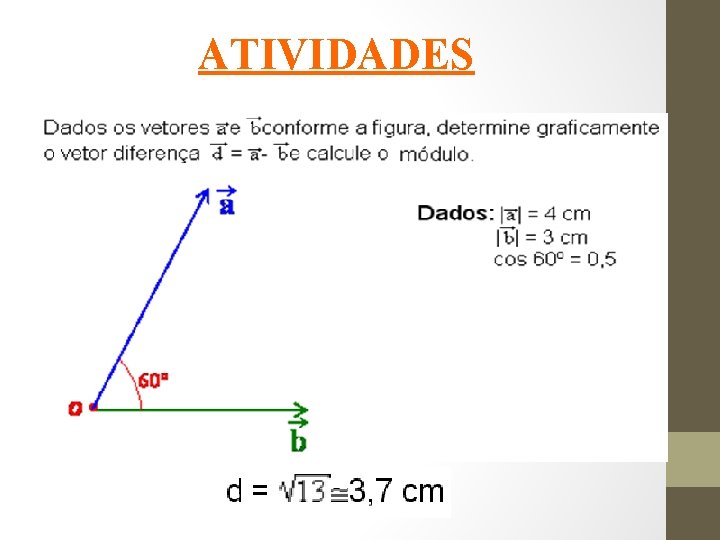
ATIVIDADES

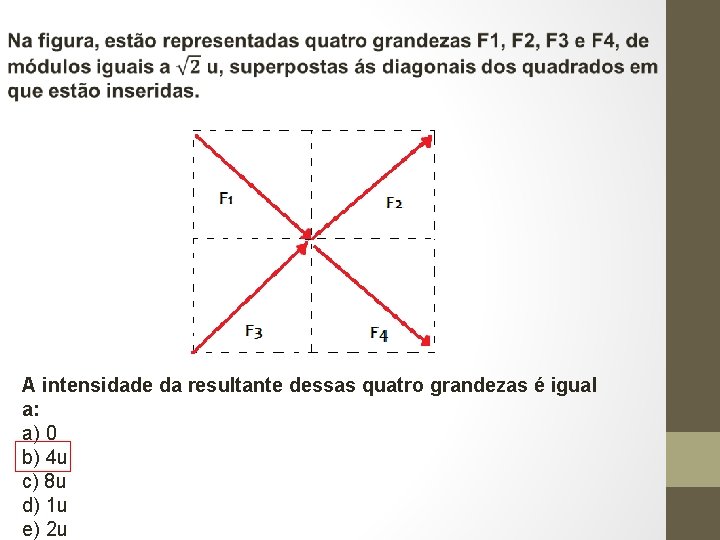
A intensidade da resultante dessas quatro grandezas é igual a: a) 0 b) 4 u c) 8 u d) 1 u e) 2 u

90°- Um caso especial Como cos 90°= 0 então

Decomposição Eu posso escrever o número 10 como a soma de dois números? ? Do mesmo modo podemos fazer com vetores, podemos escrever qualquer vetor como a soma de outros dois. Para decomposição entretanto , queremos encontrar vetores com uma característica em especial, esses vetores devem ser perpendiculares entre si

DECOMPOSIÇÃO VETORIAL • As componentes perpendiculares de um vetor, são projeções deste vetor em duas direções perpendiculares não coincidentes com a direção dele.

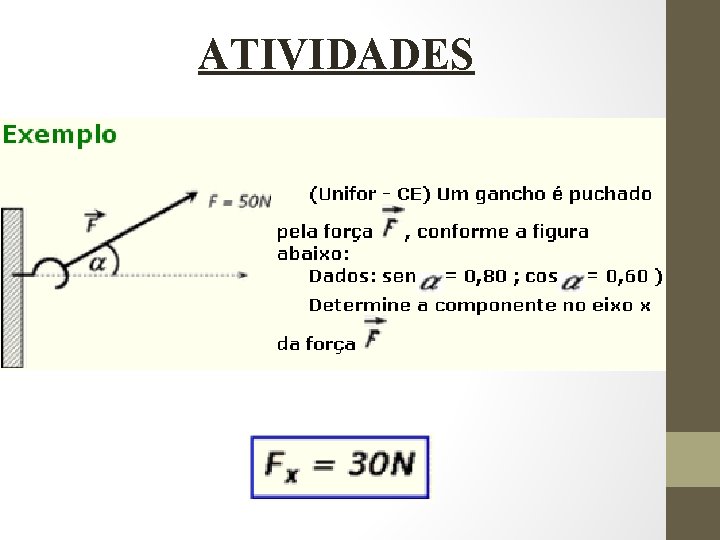
ATIVIDADES

Método da decomposição para soma de vetores • O que é mais simples de somar? ou Essa é a ideia de decompor vetores para somar. Decompomos todos os vetores (cada um com no máximo duas componentes) de modo que todas as componentes tenham apenas duas direções e que sejam perpendiculares entre si

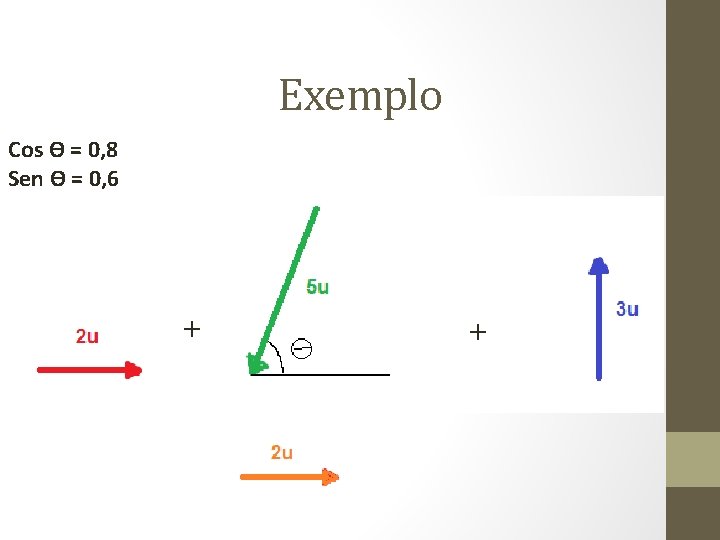
Exemplo Cos Ɵ = 0, 8 Sen Ɵ = 0, 6 + +

Aceleração da Gravidade • Corpos em queda livre sofrem uma aceleração chamada Aceleração da gravidade, o vetor dessa aceleração é sempre perpendicular ao solo e aponta para baixo. • Seu modulo na Terra é de g = 10 m/s 2

Movimento Vertical • Em um campo gravitacional uniforme , o movimento vertical de um corpo sob ação exclusiva de seu peso é uniformemente variado (MUV), pois sua aceleração escalar é constante e diferente de zero. Se a trajetória estiver orientada para cima a= -g Se a trajetória estiver orientada para baixo a = g

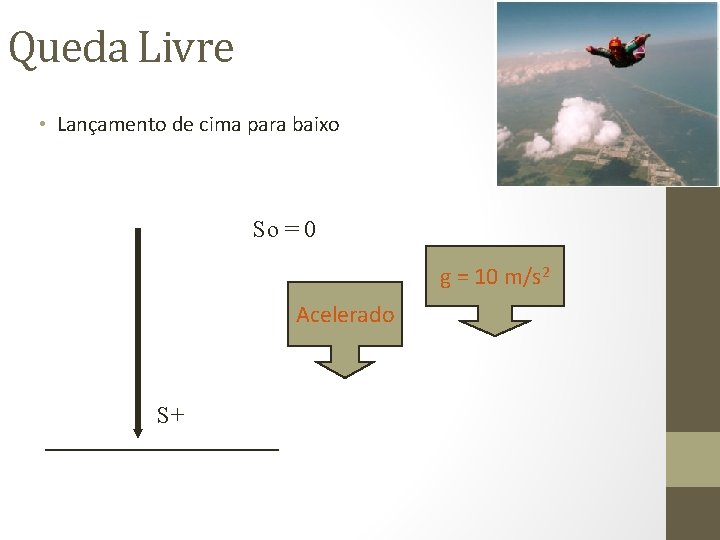
Queda Livre • Lançamento de cima para baixo So = 0 g = 10 m/s 2 Acelerado S+

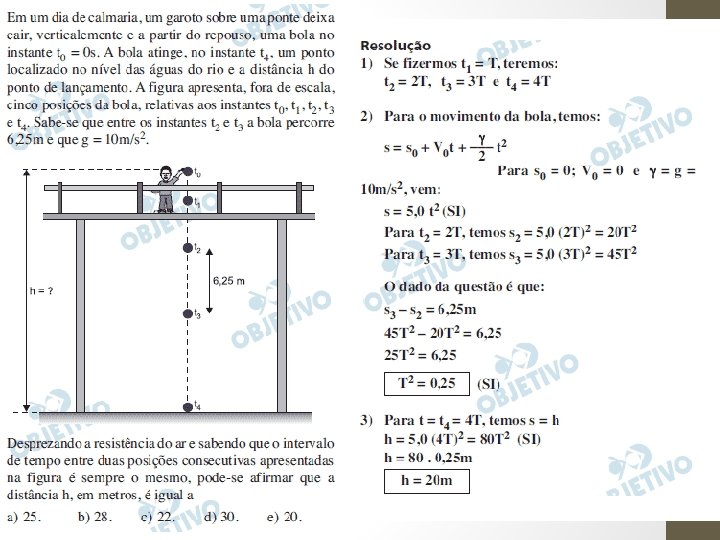
ATIVIDADES Abandona-se uma pedra do alto de um edifício e esta atinge o solo 4 s depois. Adote g=10 m/s 2 e despreze a resistência do ar. Determine. (a) a altura do edifício. (b) o módulo da velocidade da pedra quando atinge o solo.

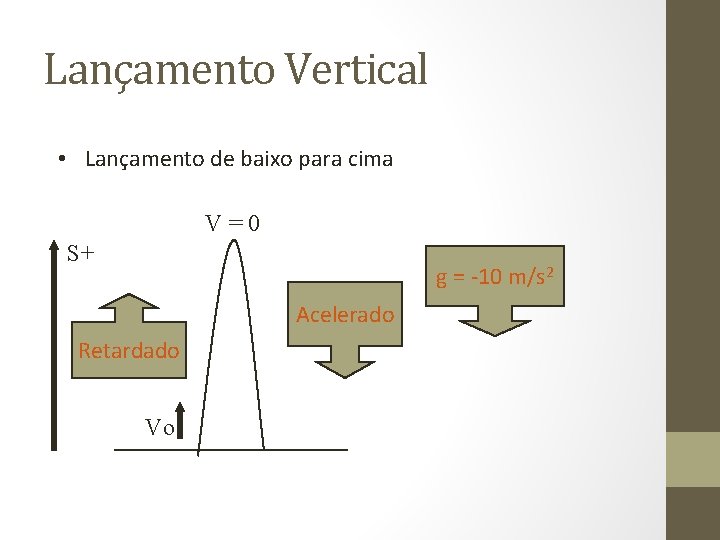
Lançamento Vertical • Lançamento de baixo para cima V=0 S+ g = -10 m/s 2 Acelerado Retardado Vo

ATIVIDADES Uma pedra A é lançada verticalmente para cima a partir do solo, com velocidade de 40 m/s. Simultaneamente, na mesma vertical, outra pedra B é abandonada a partir do repouso do alto de um edifício com 80 m de altura. Desprezando a resistência do ar e adotando g=10 m/s 2. (a) o instante em que as pedras colidem; (b) a altura, relativamente ao solo, em que ocorre a colisão.