VETORES VETORES Quantidades com magnitude e direo Magnitude

VETORES

VETORES Quantidades com magnitude e direção Magnitude: Quanto (representado pelo comprimento de uma linha) Direção: Qual direção ele aponta Pode ser represntado por um segmento de reta (seta) Exemplos: ü ü Velocidade Aceleração Deslocamento Força

É POSSÍVEL EXPRESSAR O DESLOCAMENTO

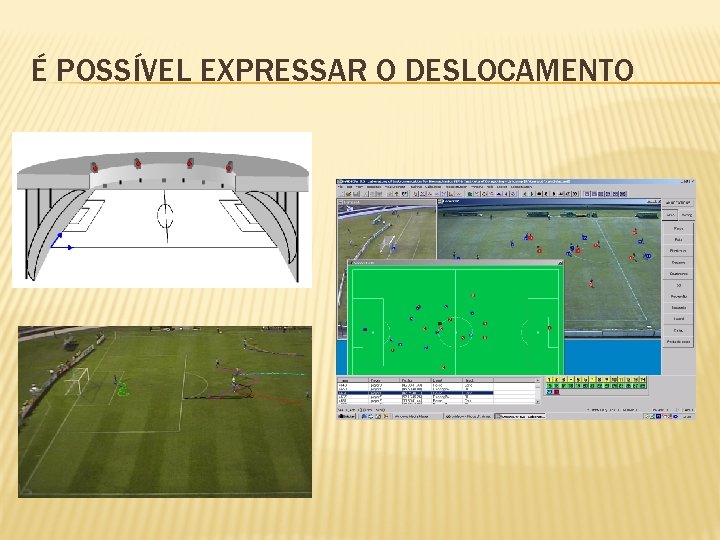
É POSSÍVEL EXPRESSAR O DESLOCAMENTO

SITUAÇÃO EXPERIMENTAL Figura 1: Câmera 1 Figura 3: Câmera 3 Figura 2: Câmera 2 Figura 4: Câmera 4

Posição em 2 dimensões Y P=(x, y) X

TRAJETÓRIA E DIST NCIA PERCORRIDA Goleiro Distância percorrida: 1969 m Lateral Distância percorrida: 4925 m

Zagueiro Distância percorrida: 4558 m Volante Distância percorrida: 4280 m

TERMINOLOGIA DE VETORES ü ü Dois ou mais vetores atuando em um pesmo ponto são denominados vetores concorrentes. A soma de dois ou mais vetores é chamada de resultante (R). ü ü ü Um vetor simples pode substituir vetores concorrentes Qualquer vetor pode ser descrito como tendo componentes “x” e “y” em um sistema de coordenadas. O processo de quebra de um vetor em componentes “x” e “y” é chamado de resolução de vetor.

TERMINOLOGIA DE VETORES ü Vetores são ditos em “equilibrio” se a soma for igual a zero. E=5 N at 180 ° R=5 N at 0°

QUAL A RESULTANTE DOS SEGUINTES VETORES? E= 10 N a 0 graus ü R = 20 N a 0 graus ü E =20 N a 45 graus ü R = 10 N a 225 graus ü ü Nem sempre os vetores estão “em linha”, mas em um ângulo entre eles

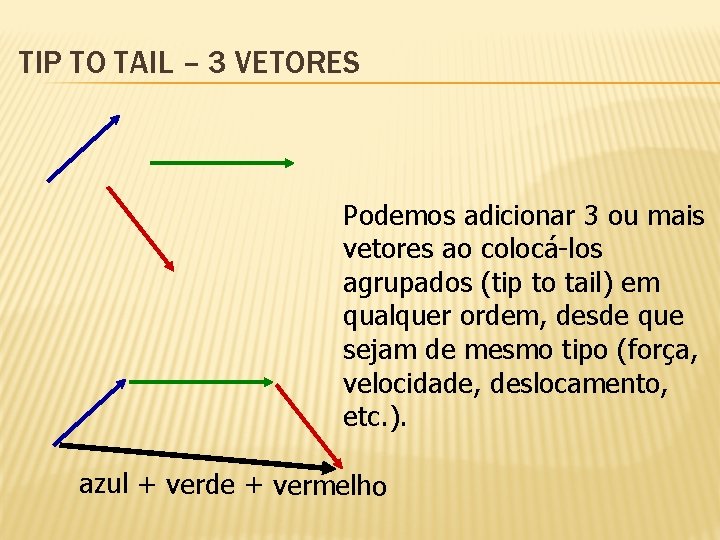
TIP TO TAIL – 3 VETORES Podemos adicionar 3 ou mais vetores ao colocá-los agrupados (tip to tail) em qualquer ordem, desde que sejam de mesmo tipo (força, velocidade, deslocamento, etc. ). azul + verde + vermelho

METODO GRAFICO DE ADIÇÃO DE VETORES ü ü Vetores podem ser desenhados em escala e a resultante pode ser determinada com uma régua e um transferidor. Vetores são adicionados ao desenhar a ponta do vetor à extremidade do segundo vector (“tip to tail”). ü ü A ordem não importa. A resultante é sempre desenhada da ponta para a extremidade do último vetor.

EXEMPLO Uma força de 50 N a 0° age concorrentemente a uma força de 20 N force a 90°. R R e são iguais em cada diagrama.

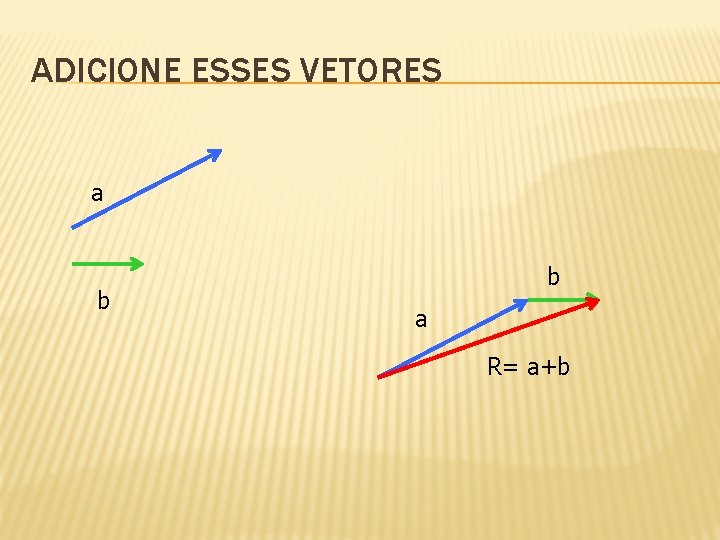
ADICIONE ESSES VETORES a b b a R= a+b

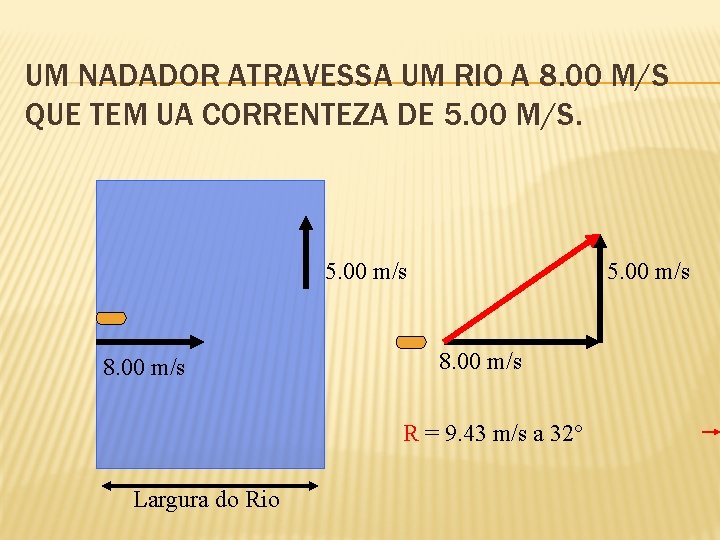
UM NADADOR ATRAVESSA UM RIO A 8. 00 M/S QUE TEM UA CORRENTEZA DE 5. 00 M/S. 5. 00 m/s 8. 00 m/s R = 9. 43 m/s a 32° Largura do Rio

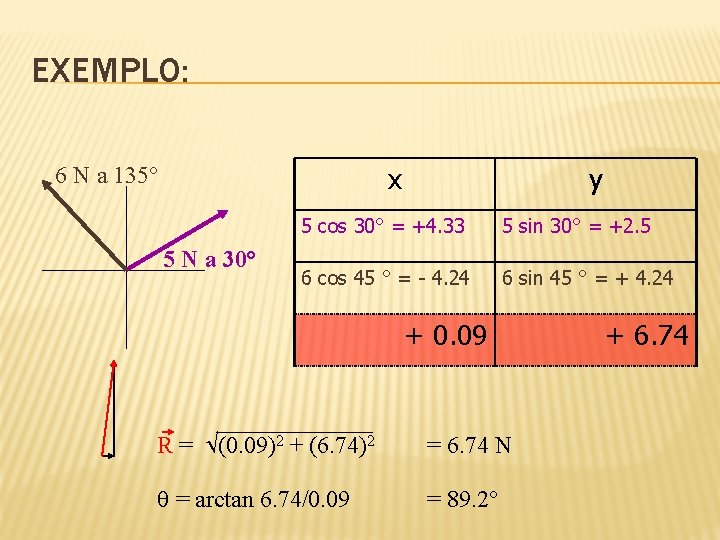
RESOLUÇÃO TRIGONOMÉTRICA sen = y / h y = h sen h y cos = x / h x x = h cos -+ ++ -- +-

EXEMPLO: 6 N a 135° x 5 N a 30° y 5 cos 30° = +4. 33 5 sin 30° = +2. 5 6 cos 45 ° = - 4. 24 6 sin 45 ° = + 4. 24 + 0. 09 R = (0. 09)2 + (6. 74)2 = 6. 74 N = arctan 6. 74/0. 09 = 89. 2° + 6. 74

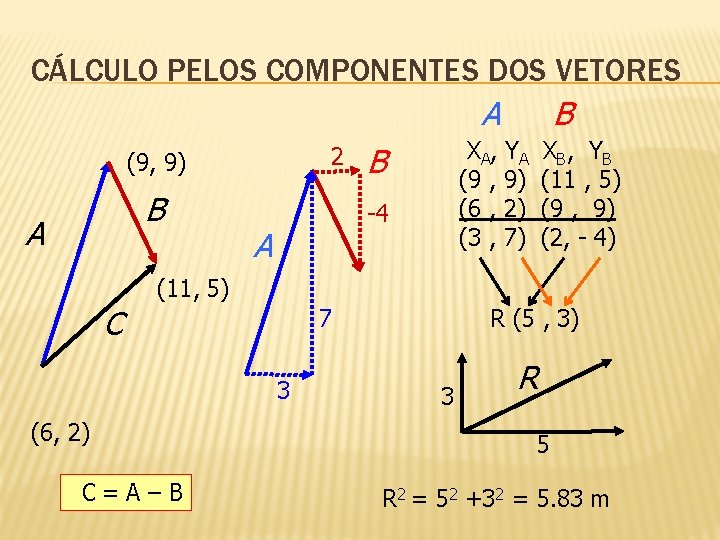
CÁLCULO PELOS COMPONENTES DOS VETORES A 2 (9, 9) B A C X A, Y A (9 , 9) (6 , 2) (3 , 7) B -4 A B X B, Y B (11 , 5) (9 , 9) (2, - 4) (11, 5) 7 3 (6, 2) C= A – B R (5 , 3) 3 R 5 R 2 = 52 +32 = 5. 83 m

ORIGEM DA LEI DOS COSSENOS cosΘ = d/b d=b. cosΘ a e= c – d e= c - b. cosΘ m senΘ= m/b m=b. senΘ b Θ c d e a 2 = m 2+e 2 (=> Norma) a 2 = (b. senΘ)2 + (c - b. cosΘ)2 a 2 = b 2. senΘ 2 + c 2 – 2 cb. cosΘ+ b 2 cosΘ 2 a 2 = b 2. senΘ 2 + b 2 cosΘ 2 + c 2 – 2 cb. cosΘ a 2 = b 2. (senΘ +cosΘ) 2 + c 2 – 2 cb. cosΘ a 2 = b 2. (1) 2 + c 2 – 2 cb. cosΘ a 2 = b 2+ c 2 – 2 cb. cosΘ

CÁLCULO DO NGULO ENTRE DOIS VETORES LEI DOS COSSENOS c 2 = a 2+ b 2 – 2|a. b|cos θ c = a-b y 1 (a-b)2 = |a 2|+|b 2| - 2|a. b|cos θ (a-b) *(a-b) = |a 2|+|b 2| - 2|a. b|cos θ a*a – a*b – b*a + b*b = |a 2|+|b 2| - 2|a. b|cos θ |a 2|- 2 (a*b) +| b 2| = |a 2|+|b 2| - 2|a. b|cos θ -(a*b) = - |a. b|cos θ (*-1) (a*b) = |a. b|cos θ c a y 2 Θ b x 1 x 2 cos θ = (a*b) /|a. b| cos Θ = a. b |a|. |b|

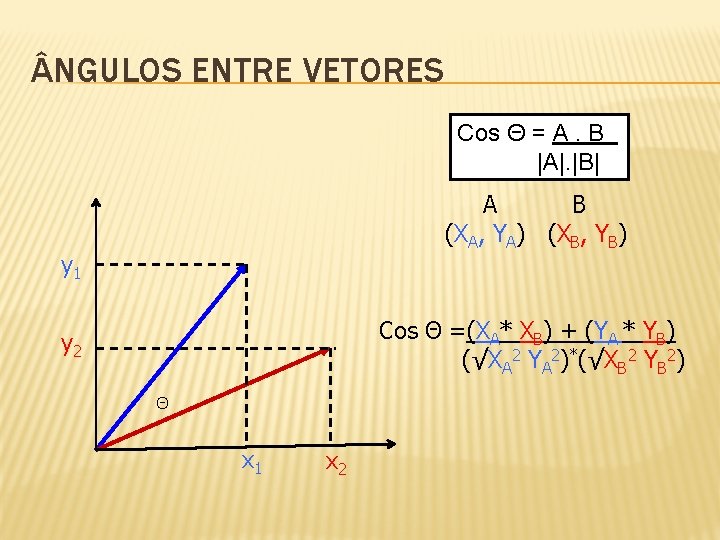
NGULOS ENTRE VETORES Cos Θ = A. B |A|. |B| A B (XA, YA) (XB, YB) y 1 Cos Θ =(XA* XB) + (YA * YB) (√XA 2 YA 2)*(√XB 2 YB 2) y 2 Θ x 1 x 2

VETORES EM 3 D Cos Θ = A. B |A|. |B| cos Θ =(XA* XB) + (YA * YB) +(ZA * ZB) (√XA 2+ YA 2 + ZA 2 )*(√XB 2 + YB 2+ ZB 2)

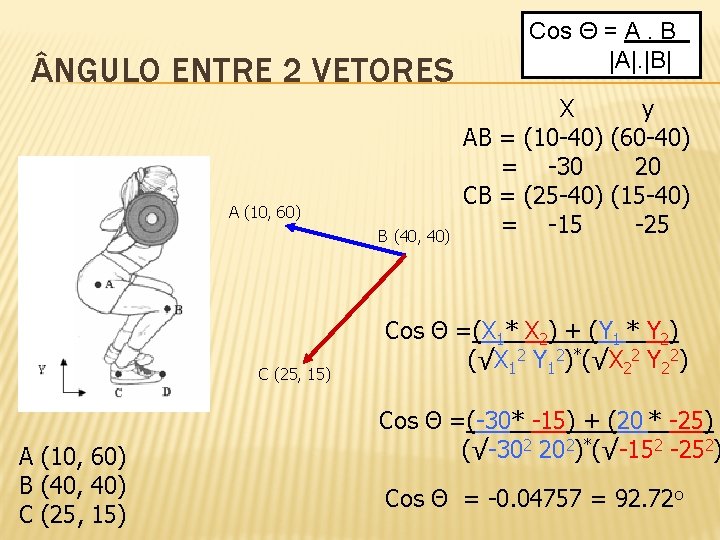
NGULO ENTRE 2 VETORES A (10, 60) B (40, 40) C (25, 15) Cos Θ = A. B |A|. |B| X y AB = (10 -40) (60 -40) = -30 20 CB = (25 -40) (15 -40) = -15 -25 Cos Θ =(X 1* X 2) + (Y 1 * Y 2) (√X 12 Y 12)*(√X 22 Y 22) Cos Θ =(-30* -15) + (20 * -25) (√-302 202)*(√-152 -252) Cos Θ = -0. 04757 = 92. 72 o