Diferencijalni raun IZVOD FUNKCIJE Problemi tangente i brzine

Diferencijalni račun IZVOD FUNKCIJE

• • Problemi tangente i brzine, ekstrema, tj. minimuma i maksimuma postepeno su podsticali nastajanje pojma izvoda. Mnogi matematičari još od antičke Grčke uspevali su da reše neke od ovih problema za pojedinačne slučajeve. Tek kada je Dekart definisao metodu koordinata omogućeno je da se krive predstavljaju jednačinama, tako da je stvoren osnovni preduslov za pojavu opšte metode za analitičko rešavanje problema , odnosno za definisanje pojma izvoda. Problem tangente prvi je rešio nemački matematičar i filozof Lajbnic definišući novu oblast matematike pod nazivom diferencijalni račun. U isto vreme Njutn je definisao izvod kao posledicu istrživanja fenomena kretanja. To su bile dve idejno i metodolški različite koncepcije koje su dovele do istog rezultata. Danas, diferencijalni račun, predstavlja nezaobilazno sredstvo u rešavanju mnogih problema savremene nauke i tehnike.

Priraštaj funkcije •

Izvod funkcije •

OSNOVNA PRAVILA DIFERENCIRANJA

Tablica izvoda

Naći izvod funkcije

• Naći drugi izvod

• Naći izvod funkcija

Složene funkcije


• Naći izvod složenih funkcija

IZVODI VIŠEG REDA •

Primer 4 Odrediti drugi izvod funkcije Rešenje:
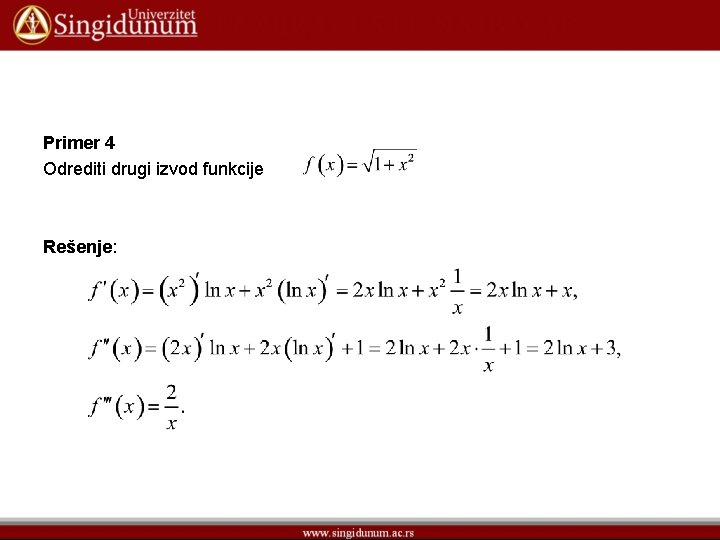
Primer 4 Odrediti drugi izvod funkcije Rešenje:

LOPITALOVA TEOREMA Ako su funkcije f(x) i g(x) diferencijabilne u nekoj okolini tačke a , pri čemu je tada je:

Ako funkcije f(x) i g(x) imaju n- te izvode koji su neprekidni u tački a i ako je onda je

Primer 8 Primenom Lopitalove teoreme odrediti granične vrednosti:

Primer 9 Primenom Lopitalove teoreme odrediti granične vrednosti:

Primer 10 Primenom Lopitalove teoreme odrediti granične vrednosti

Primer 11 Primenom Lopitalove teoreme odrediti granične vrednosti:
- Slides: 21