Vetores II Combinao Linear n Dados n vetores

Vetores II

Combinação Linear n Dados n vetores v 1, v 2, . . . , vn e n escalares a 1, a 2, . . . , an n o vetor v = a 1 v 1 + a 2 v 2+. . . + anvn, é a combinação linear dos vetores v 1, v 2, . . . , vn com coeficientes a 1, a 2, . . . , an

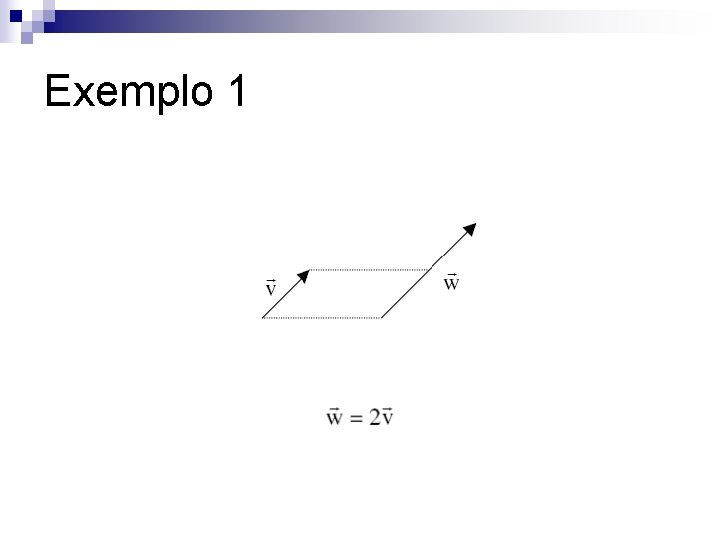
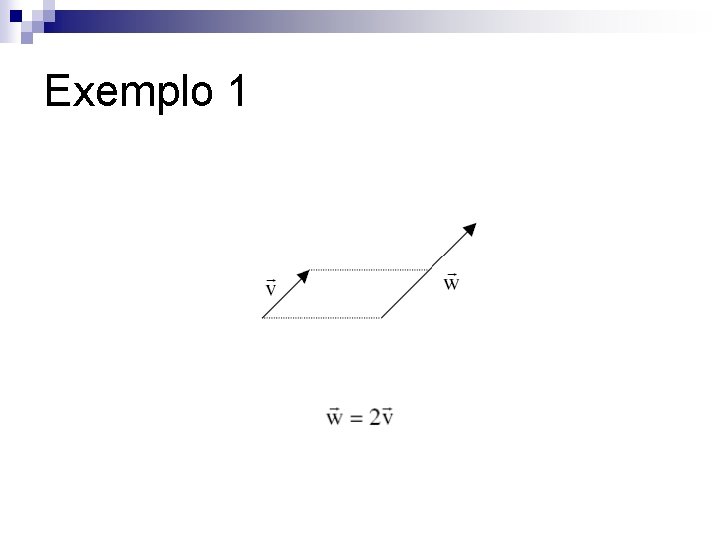
Exemplo 1

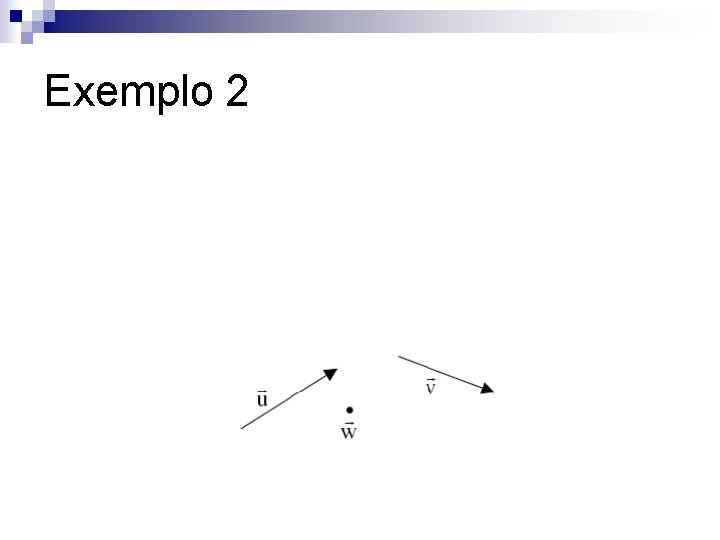
Exemplo 2

Exemplo 2 n Como w=0=0 u + 0 v, dizemos que 0 é combinação linear de u e v, com coeficientes zeros

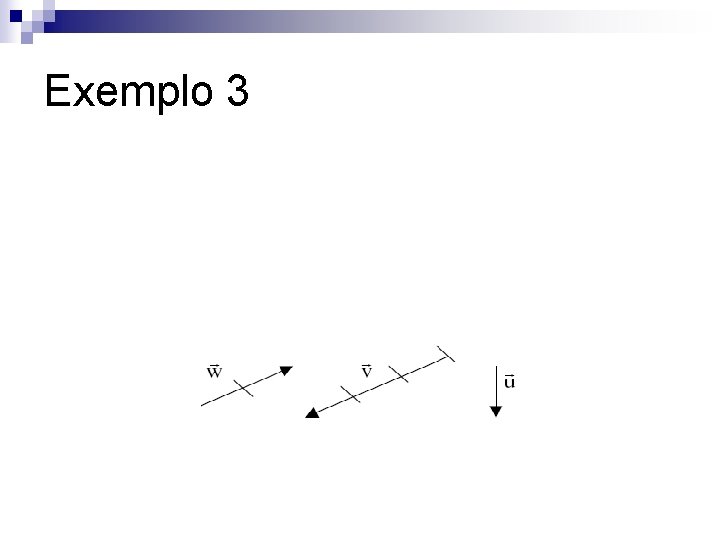
Exemplo 3

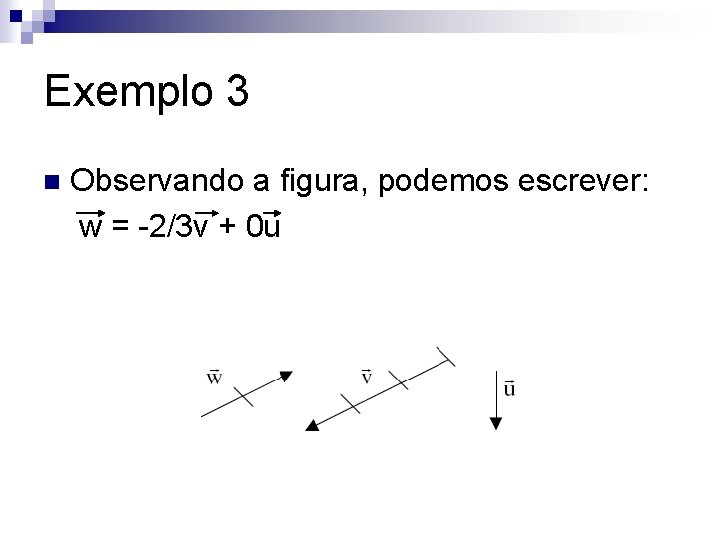
Exemplo 3 n Observando a figura, podemos escrever: w = -2/3 v + 0 u

Exemplo 4 Observe que o vetor AC = AB + AD possui a mesma direção que a diagonal AC n Se | AB| = | AD|, este paralelogramo será um losango n

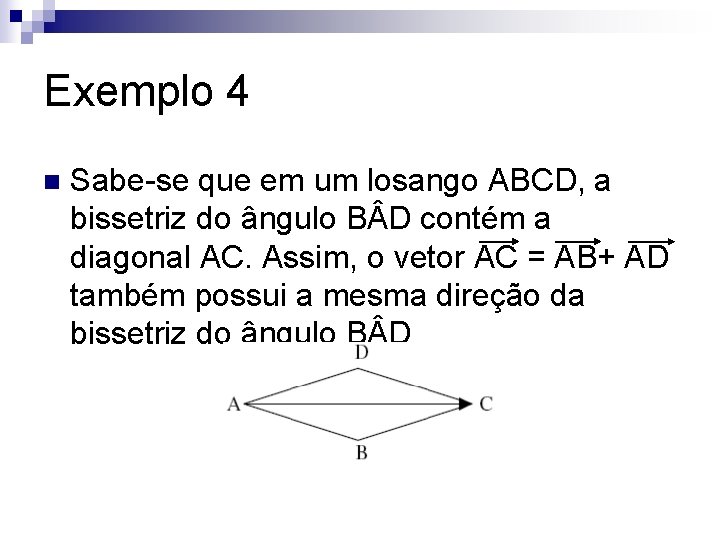
Exemplo 4 n Sabe-se que em um losango ABCD, a bissetriz do ângulo B D contém a diagonal AC. Assim, o vetor AC = AB+ AD também possui a mesma direção da bissetriz do ângulo B D

Exemplo 4 n Se | AB| ≠ | AD|, o vetor AC não possui a mesma direção da bissetriz de B D. Para obter um vetor que possua a mesma direção da bissetriz de B D basta usar o vetor v = t. AB°+ t. AD° , t є R*

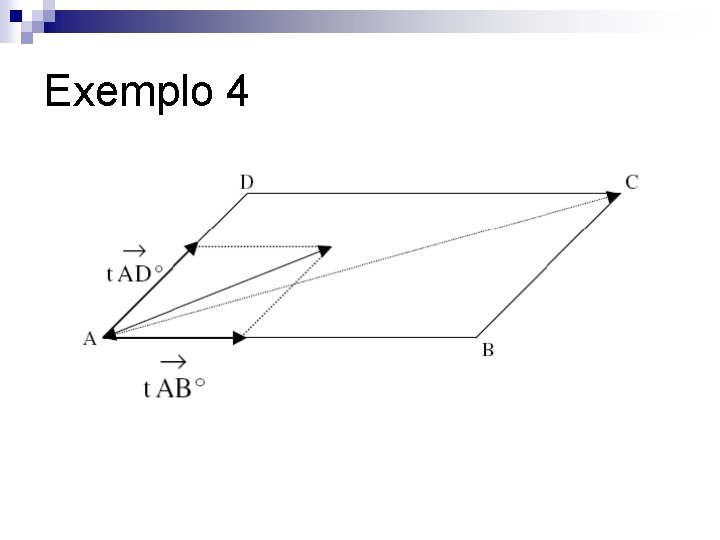
Exemplo 4

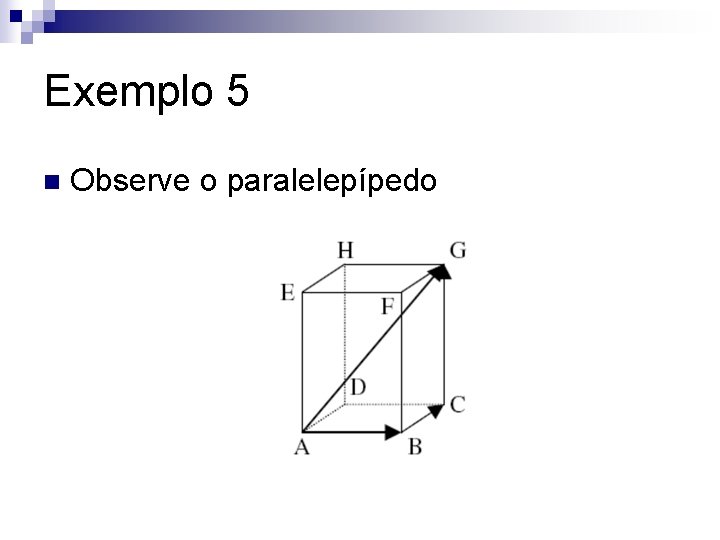
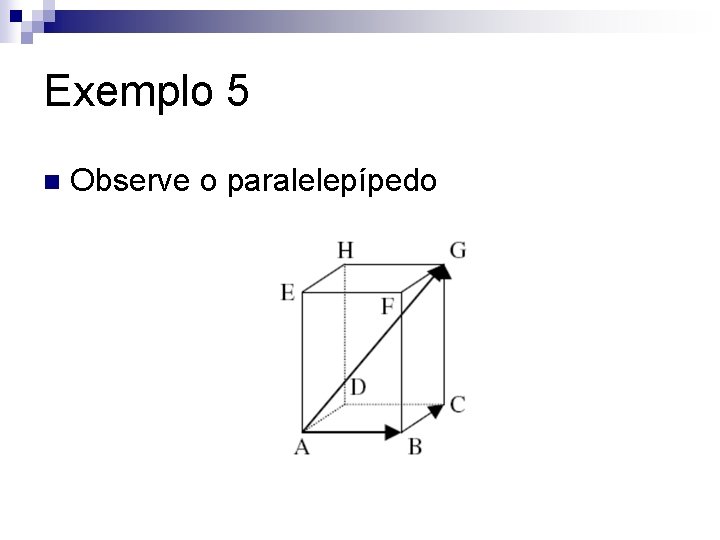
Exemplo 5 n Observe o paralelepípedo

Exemplo 5 AG = AB + BC + CG Dizemos então que AG é combinação linear dos vetores AB, BC e CG n Como BC = AD e CG = AE, então: AG = AB+ AD+ AE. Assim, podemos também dizer que AG é combinação linear dos vetores AB, AD e AE n

Paralelismo Definição: Os vetores v 1, v 2, . . . , vn são colineares (paralelos), se possuem representantes em uma mesma reta. Neste caso indicamos v 1 // v 2// v 3//. . . // vn n No exemplo 1, temos v // w, e no exemplo 2 temos w // u e w // v, embora u e v não sejam paralelos n

Exemplo 1

Paralelismo Definição: Os vetores v 1, v 2, . . . , vn são colineares (paralelos), se possuem representantes em uma mesma reta. Neste caso indicamos v 1 // v 2// v 3//. . . // vn n No exemplo 1, temos v // w, e no exemplo 2 temos w // u e w // v, embora u e v não sejam paralelos n

Exemplo 2

Propriedade 1 n n Os vetores u e v são paralelos se, e somente se, podemos escrever um deles como combinação linear do outro. Prova: Considere os seguintes casos: ¨ 1) u = 0 = v; u = tv, tєR ¨ 2) u =0 e v ≠ 0; temos u = 0 v ¨ 3) u ≠ 0 e v ≠ 0. Como u // v, temos uº = ± vº. Daí, | uº = ± | u | (v /| v |) , ou seja, u = ±(| u |/| v |) v. Assim, se u e v têm mesmo sentido podemos escrever u = (| u |/| v |) v. E se u e v têm sentidos contrários temos u = -(| u |/| v |) v

n Por outro lado, suponha que podemos escrever u como combinação linear de v, ou seja, u = tv. n Pela definição de produto de um número real por vetor, temos que u e v têm a mesma direção, logo são paralelos.

Vetores Coplanares Os vetores v 1, v 2, . . . , vn são coplanares, se possuem representantes em um mesmo plano n Observe que a colinearidade de vetores é um caso particular da coplanaridade de vetores n Nos exemplos de 1 a 4, os vetores envolvidos são coplanares n

Exemplo 1

Exemplo 2

Exemplo 3

Exemplo 4 Observe que o vetor AC = AB + AD possui a mesma direção que a diagonal AC n Se | AB| = | AD|, este paralelogramo será um losango n

Exemplo 5 n Observe o paralelepípedo

Propriedade 1 Os vetores u, v e w são coplanares se, e somente se, podemos escrever um deles como combinação linear dos outros. n Prova: 3 possíveis casos n

Caso 1 Um deles sendo o vetor nulo, digamos =0 n Podemos escrever: u= 0 v + 0 w. n u

Caso 2 n Dois deles são paralelos, digamos u // v e v≠ 0 n Assim, u = mv + 0 w, m R

Caso 3 Quaisquer dois desses vetores não paralelos n Considere a figura, onde α é um plano que contém representantes dos vetores u, v e w n

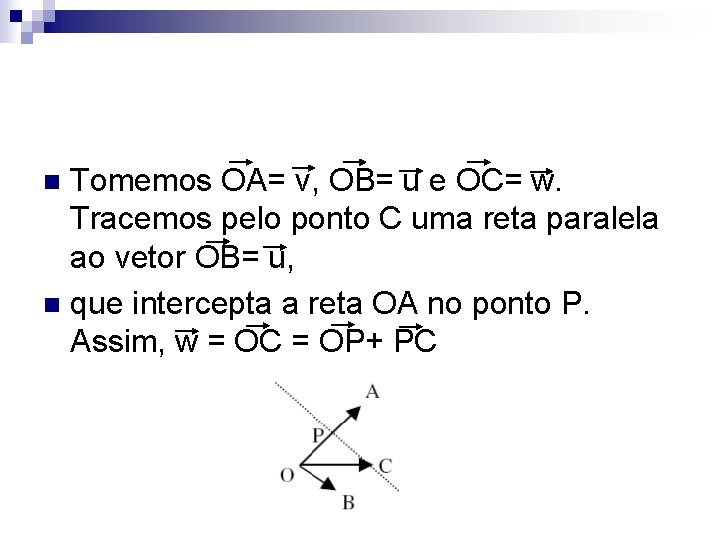
Tomemos OA= v, OB= u e OC= w. Tracemos pelo ponto C uma reta paralela ao vetor OB= u, n que intercepta a reta OA no ponto P. Assim, w = OC = OP+ PC n

Como OP // OA e PC //OB temos: w = mv + nu, m, n R n Por outro lado, suponhamos que w = mv + nu, n, m R. Assim, pela definição de adição de vetores, temos que u, v e w são coplanares. n

Dependência Linear Um Vetor: v é linearmente dependente, se v = 0 n Dois vetores: u e v são linearmente dependentes se eles são paralelos n Três vetores: u, v e w são linearmente dependentes se eles são coplanares n

Dependência Linear n Mais de três vetores do espaço (R 3 ), são sempre linearmente dependentes n Quando os vetores do espaço não são linearmente dependentes (LD), dizemos que são linearmente independentes (LI)

Exemplo

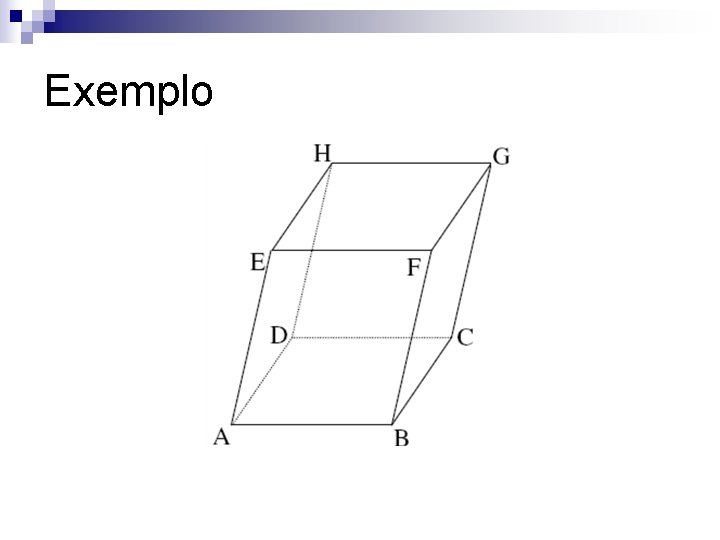
Exemplo 1)AB é ? n 2)AB+BC+CA é ? n 3)AD e AE são ? n 4) AB e ½ AB são ? n

Exemplo 1)AB é LI n 2)AB+BC+CA é LD n 3)AD e AE são LI n 4) AB e ½ AB são LD n

Exemplo 5)AB, AD e AE são ? n 6)AE, AB e DC são ? n 7)AB, AD e FF são ? n 8)AB, BF, BC e AG são ? n

Exemplo 5)AB, AD e AE são LI n 6)AE, AB e DC são LD n 7)AB, AD e FF são LD n 8)AB, BF, BC e AG são LD n

Propriedades - 1 Se um vetor v é LI, então dado u // v, temos que existe um único escalar m tal que u=mv n Como v é LI e u // v pela propriedade 1 de Paralelismo, temos que u=mv n Suponha u=m’v => (m-m’)v = 0 n

Propriedades - 2 n Se dois vetores v 1 e v 2 são LI, então dado v coplanar com v 1 e v 2, temos que existe um único par de escalares (m, n), tal que v = mv 1 + nv 2

Propriedade – 2 (prova) Como v, v 1 e v 2 são coplanares e, v 1 e v 2 são LI, temos pela prova da propriedade 1 de vetores coplanares, que v= mv 1 + nv 2 n Para mostrar que esses escalares são únicos, suponha que existam m’e n’, tais que: v= m’v 1+ n’v 2 n Então (m- m’ )v 1 + (n- n’)v 2=0 n

Propriedade – 2 (prova) n Se m – m’≠ 0 , podemos escrever v 1= (n-n’)/(m-m’) v 2 n Daí, v 1 // v 2, o que contradiz o fato de v 1 e v 2 serem LI. Logo, m – m’ = 0 , m = m’ n A prova para n e n’ é análoga

Propriedade - 3 n Se três vetores v 1, v 2 e v 3 são LI, então dado um vetor v qualquer, temos que existe único trio de escalares (m, n, p), tal que v = mv 1+ nv 2+ pv 3

Propriedade – 3 (Prova) Suponha que v 1, v 2 e v 3 são LI, temos então os seguintes casos: n 1) v=0. Logo, v= 0 v 1+0 v 2+0 v 3 n n 2) v paralelo a um dos vetores, digamos v//v 1. Então v=mv 1+0 v 2+0 v 3

Propriedade – 3 (Prova) n 3) v coplanar com dois dos vetores, digamos v, v 1 e v 2 são coplanares. Assim, v=mv 1+nv 2 = mv 1+ nv 2+ 0 v 3 n 4) v não é coplanar com quaisquer dois dos vetores (próximo slide)

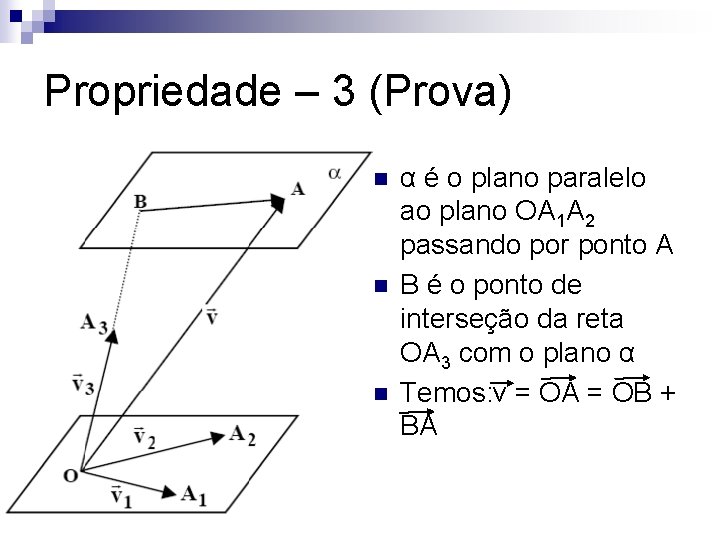
Propriedade – 3 (Prova) n n n α é o plano paralelo ao plano OA 1 A 2 passando por ponto A B é o ponto de interseção da reta OA 3 com o plano α Temos: v = OA = OB + BA

Propriedade – 3 (Prova) Como OB // v 3 r e BA é coplanar com v 1 e v 2, temos: OB=pv 3, BA=mv 1+nv 2 n Logo v=mv 1+nv 2+pv 3 n n Para provar que estes escalares são únicos usamos a mesma metodologia da prova da propriedade 2

Base – Coordenadas de Vetor Dado um vetor v LI, dizemos que { v } é uma base para o conjunto de vetores paralelos a v n Dados dois vetores v 1 e v 2 LI, dizemos que { v 1, v 2 } é uma base para o conjunto de vetores coplanares com v 1 e v 2 n

Base – Coordenadas de Vetor Dados três vetores v 1, v 2 e v 3 LI, dizemos que { v 1, v 2 , v 3 } é uma base para o conjunto de vetores do espaço ( R 3) n Dizemos que uma base é ortogonal, quando seus vetores são ortogonais quando comparados dois a dois n

Base – Coordenadas de Vetor Dizemos que uma base é ortonormal, se ela for ortogonal e seus vetores unitários n Costumamos representar uma base ortonormal por { i , j, k} n Fixada uma base { v 1, v 2, v 3} do espaço, pela propriedade 3 de Dependência linear, todo vetor v, temos v = mv 1+ nv 2+ pv 3, onde m, n e p são únicos n

Base – Coordenadas de Vetor n n n Dizemos que mv 1 , nv 2 e pv 3 são as componentes de v na direção dos vetores v 1, v 2 e v 3, respectivamente Os escalares m, n e p são as coordenadas de v em relação à base {v 1, v 2 , v 3} Geralmente, representamos o vetor v através de suas coordenadas, ou seja, v = (m, n, p)

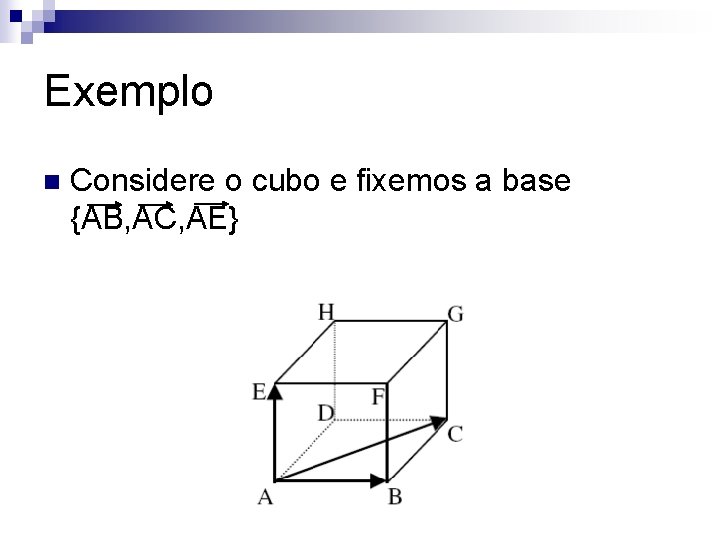
Exemplo n Considere o cubo e fixemos a base {AB, AC, AE}

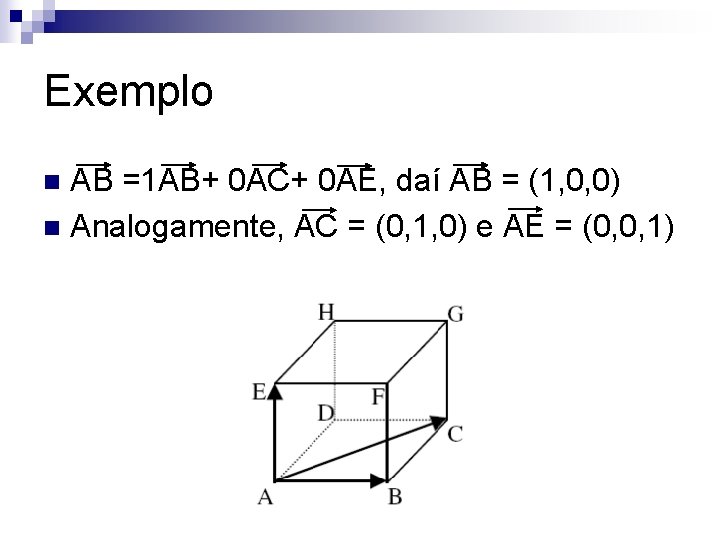
Exemplo AB =1 AB+ 0 AC+ 0 AE, daí AB = (1, 0, 0) n Analogamente, AC = (0, 1, 0) e AE = (0, 0, 1) n

Exemplo n Podemos concluir então que, dada uma base qualquer {v 1, v 2, v 3}, as coordenadas desses vetores em relação a esta base são: v 1= (1, 0, 0), v 2 =(0, 1, 0) e v 3= (0, 0, 1)

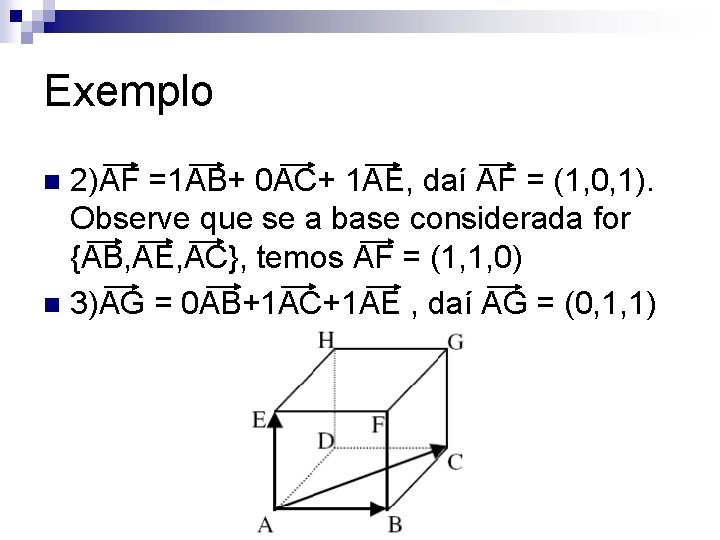
Exemplo 2)AF =1 AB+ 0 AC+ 1 AE, daí AF = (1, 0, 1). Observe que se a base considerada for {AB, AE, AC}, temos AF = (1, 1, 0) n 3)AG = 0 AB+1 AC+1 AE , daí AG = (0, 1, 1) n

Exemplo 2 n n Consideremos v = (-1, 1, 1) em relação base {AB, AC, AE} do exemplo anterior. Assim, v = -AB + AC + AE = AH Analogamente ao que foi feito para o conjunto dos vetores no espaço, podemos fazer para conjuntos de vetores coplanares e colineares. Assim, um vetor num conjunto de vetores coplanares tem duas coordenadas e um vetor num conjunto de vetores colineares tem uma coordenada

Propriedade 1 Seja {v 1, v 2, v 3} uma base do espaço. Considere os vetores u, v e w, dados por suas coordenadas em relação a esta base n 1) Se u=(a 1, a 2 , a 3), v=(b 1, b 2 , b 3) e t є R então: n ¨ a) u = v a 1=b 1, a 2 =b 2 e a 3=b 3 ¨ b) u + v = ( a 1 + b 1, a 2 + b 2, a 3 + b 3) ¨ c) t u = (t a 1, t a 2 , t a 3 )

Propriedade 1 (prova) n a) Como u = a 1 v 1+a 2 v 2+a 3 v 3 e v=b 1 v 1+b 2 v 2 +b 3 v 3, temos: ¨ (a 1 -b 1)v 1+ (a 2 -b 2 ) v 2+ (a 3 - b 3 ) v 3= 0 n Daí, 0=(a 1 -b 1, a 2 - b 2 , a 3 - b 3 ) n Logo, a 1 -b 1=0 , a 2 -b 2=0 e a 3 - b 3=0

Propriedade 1 (prova) n De maneira análoga podemos mostrar os itens b) e c) n Observe que os vetores u = (0, 0, 0) e v = ( b 1, b 2 , b 3) são LD, visto que o vetor nulo é paralelo a todo vetor do espaço

Propriedade 2 Sejam u = ( a 1, a 2 , a 3) e v = (b 1, b 2, b 3) vetores não nulos, u e v são LD se, e somente se, existe um t є R tal que : n a 1 = t b 1 n a 2 = t b 2 n a 3 = t b 3 n

Propriedade 2 (prova) Se u e v são LD, então u // v. Como v é LI, podemos escrever: u = t v , ou seja, n a 1 = t b 1 n a 2 = t b 2 n a 3 = t b 3 n

Propriedade 2 (prova) Por outro lado, se existe t є R , tal que n a 1 = t b 1 n a 2 = t b 2 n a 3 = t b 3 n então u = t v. Logo u // v e portanto u e v são LD n

Propriedade 3 n Três vetores u=(a 1, a 2, a 3), v=(b 1, b 2, b 3) e w=(c 1, c 2, c 3) são LD se, e somente se

Propriedade 3 Esta propriedades pode ser demonstrada através de propriedades de determinantes n Concluímos que se t não existe na propriedade 2, ou se Delta é diferente de zero, na propriedade 3, temos que os vetores considerados são LI n

Exercícios Considere u = 2 i –j +2 k, v= 5 i +5 j -2 k e w =3 i +6 j n Verifique se os vetores são LD em cada um dos itens nu nuev n 0 n

Exercício ue 0 n u e (4, -2, 4) n u, v e w n u, v, (1, 2, 3) e (2, 1, 4) n u, v, (7, 4, 0) n

Exercícios Considere u = 2 i –j +2 k, v= 5 i +5 j -2 k e w =3 i +6 j n Verifique se os vetores são LD em cada um dos itens n u -> LI n u e v -> LI n 0 -> LD n

Exercício u e 0 -> LD n u e (4, -2, 4) -> LD n u, v e w -> LI n u, v, (1, 2, 3) e (2, 1, 4) ->LD n u, v, (7, 4, 0) -> LD n

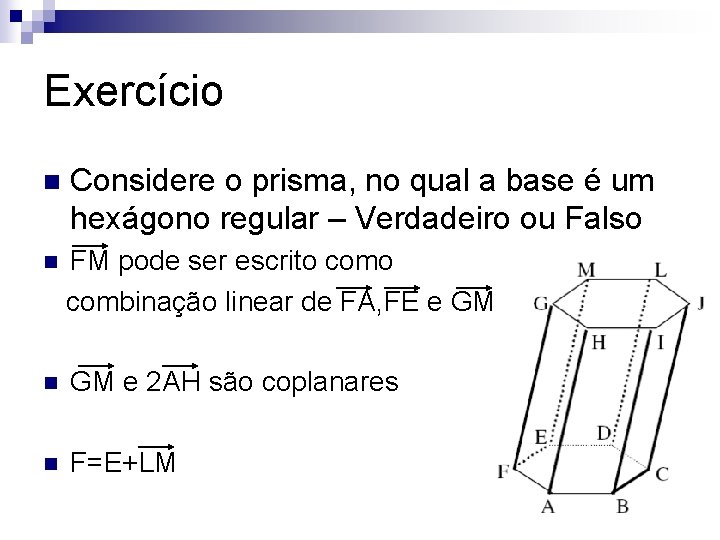
Exercício n Considere o prisma, no qual a base é um hexágono regular – Verdadeiro ou Falso n FM pode ser escrito combinação linear de FA, FE e GM n GM e 2 AH são coplanares n F=E+LM

Sistemas de Coordenadas Cartesianas n Um sistema de coordenadas cartesianas no espaço é um conjunto formado por um ponto O e uma base { v 1, v 2, v 3} e denotado por {O, v 1, v 2, v 3}

Sistema de coordenadas n O ponto O é chamado origem do sistema e os eixos que passam por O e tem as direções de v 1, v 2 e v 3, respectivamente, são chamados de eixo das abscissas, ordenadas e cotas.

Sistema de coordenadas n n n Considere um sistema de coordenadas cartesianas {O, v 1, v 2, v 3} e seja P um ponto arbitrário do espaço Chamamos coordenadas do ponto P em relação ao sistema {O, v 1, v 2, v 3}, as coordenadas do vetor OP Se OP = (a 1, a 2 , a 3), então P=(a 1, a 2 , a 3). Os números a 1, a 2 , a 3 são denominados abscissa, ordenada e cota do ponto P, respectivamente

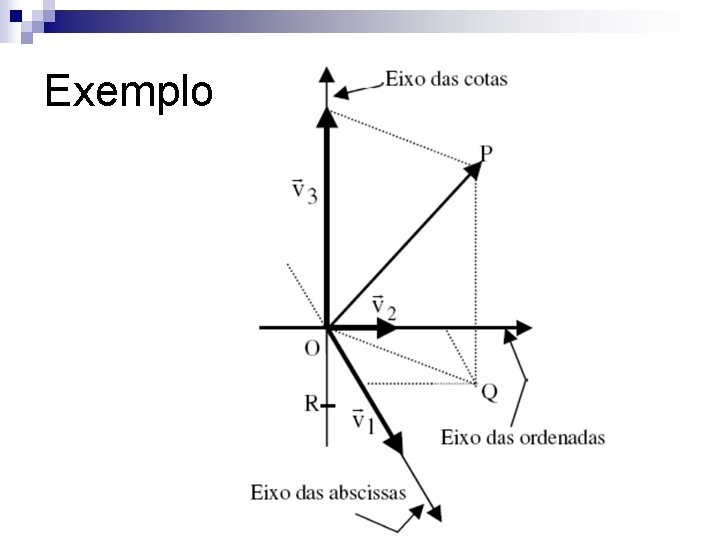
Exemplo

Exemplo OP=1/2 v 1+2 v 2+v 3 n OP=(1/2, 2, 1) logo P=(1/2, 2, 1) n OQ=(1/2, 2, 0) n OR= -2/3 v 3 = (0, 0, -2/3) n OO=(0, 0, 0) n

Propriedade 1 n n Considere um sistema de coordenadas {O, v 1, v 2 , v 3}, v = (a, b, c), P(x 1, y 1, z 1) e Q(x 2 , y 2 , z 2 ): QP=(x 1 -x 2, y 1 -y 2, z 1 -z 2 )

Propriedade 1 (prova) Escrevemos o vetor QP como combinação linear dos vetores OQ e OP n QP=-OQ+OP n QP=-(x 2 , y 2 , z 2 )+ (x 1, y 1, z 1) n QP=(x 1 -x 2, y 1 -y 2, z 1 -z 2 ) n

Propriedade 2 n P+v=A=(x 1+a, y 1+b, z 1+c)

Propriedade 2 (Prova) Utilizando a definição de soma de um ponto com um vetor, temos que PA=v n Assim, o vetor OA=OP+PA=(x 1+a, y 1+b, z 1+c) n

Propriedade 3 n O ponto médio de PQ é o ponto M dado por n M=((x 1+x 2)/2, (y 1+y 2)/2, (z 1+z 2)/2)

Propriedade 3 (prova) Escrevendo OM=OQ+QM n OM= OQ+1/2 QP n Representando os vetores OQ e QP através de suas coordenadas, obtemos: n n OM=(x 2, y 2, z 2)+ ½(x 1 -x 2, y 1 -y 2, z 1 -z 2)

Exemplo 2 Considere o paralelogramo ABCD, onde A=(1, 0, 2), B=(1, -1, 2), C(0, 2, -2) n Devemos determinar as coordenadas dos vetores AB e BC, do vértice D e do ponto médio de AB n

Exemplo 2 Aplicando as propriedades temos: n AB = (1 -1, -1 - 0, 2 - 2) = (0, -1, 0) n BC = (-1, 3, -4) n D = A + AD = A + BC = (0, 3, -2) n M=(1, -1/ 2, 2) n