Chapter 9 Parallel Lines Eleanor Roosevelt High School





















































































- Slides: 142

Chapter 9 Parallel Lines Eleanor Roosevelt High School Chin-Sung Lin

ERHS Math Geometry Angles Formed by Intersecting Lines Mr. Chin-Sung Lin

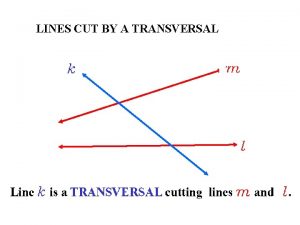
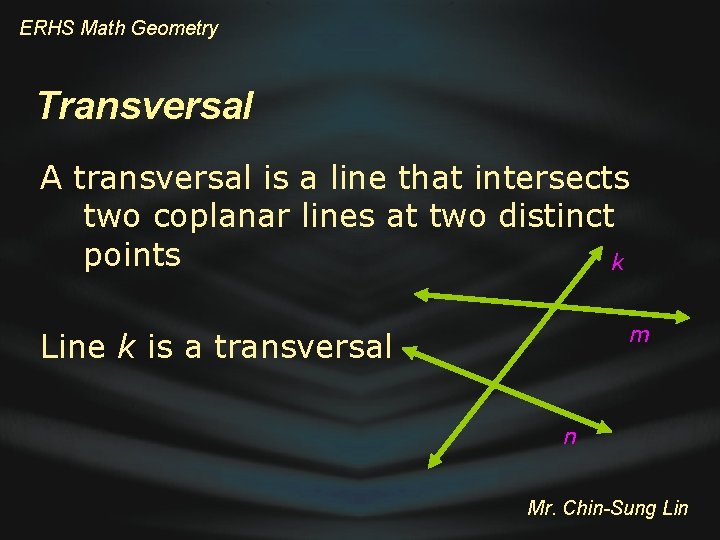
ERHS Math Geometry Transversal A transversal is a line that intersects two coplanar lines at two distinct points k m Line k is a transversal n Mr. Chin-Sung Lin

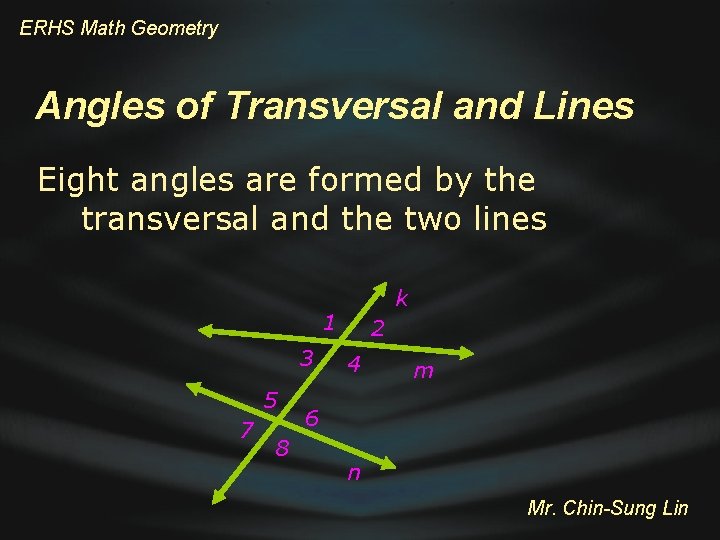
ERHS Math Geometry Angles of Transversal and Lines Eight angles are formed by the transversal and the two lines k 1 3 5 7 8 2 4 m 6 n Mr. Chin-Sung Lin

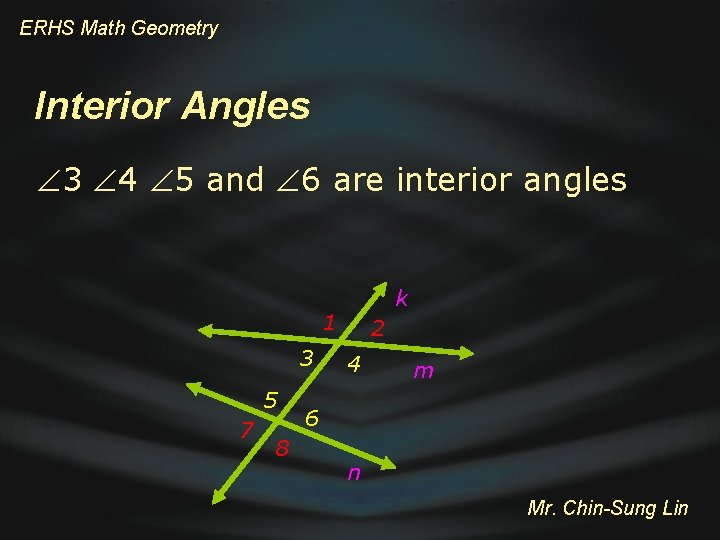
ERHS Math Geometry Interior Angles 3 4 5 and 6 are interior angles k 1 3 5 7 8 2 4 m 6 n Mr. Chin-Sung Lin

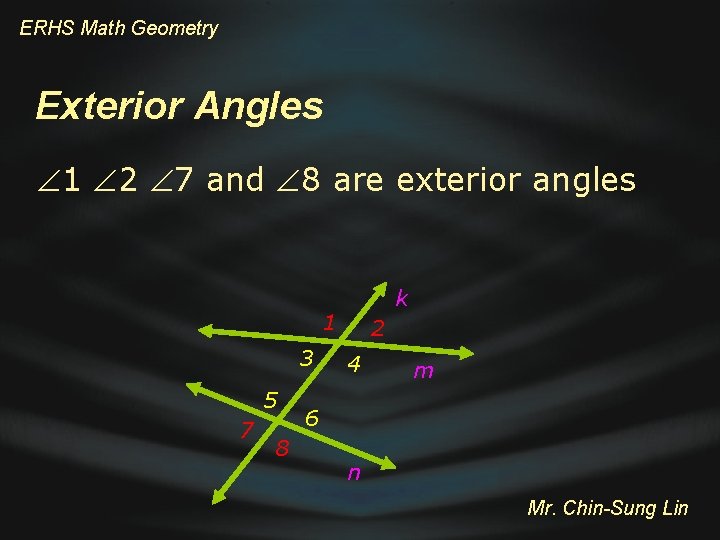
ERHS Math Geometry Exterior Angles 1 2 7 and 8 are exterior angles k 1 3 5 7 8 2 4 m 6 n Mr. Chin-Sung Lin

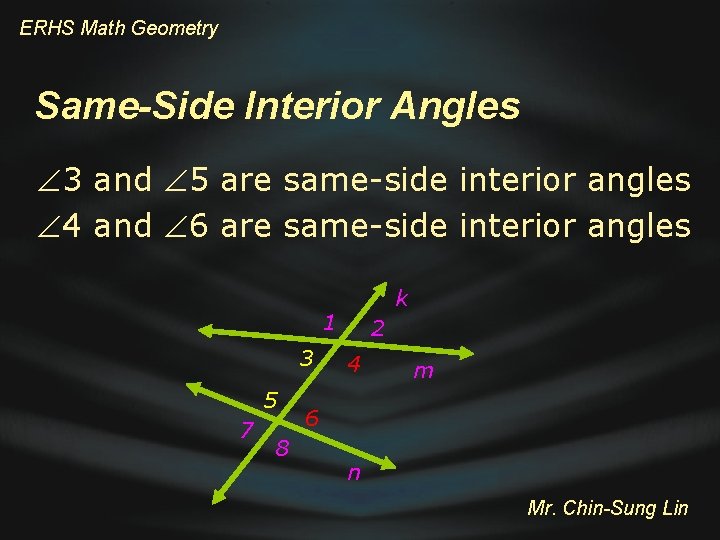
ERHS Math Geometry Same-Side Interior Angles 3 and 5 are same-side interior angles 4 and 6 are same-side interior angles k 1 3 5 7 8 2 4 m 6 n Mr. Chin-Sung Lin

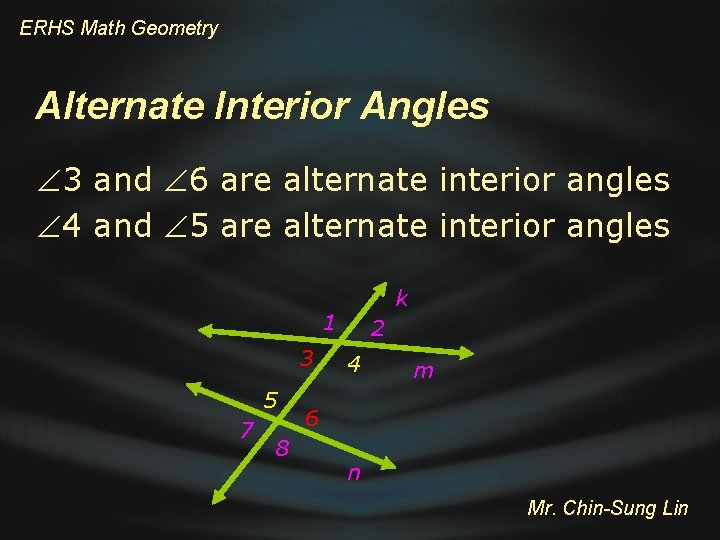
ERHS Math Geometry Alternate Interior Angles 3 and 6 are alternate interior angles 4 and 5 are alternate interior angles k 1 3 5 7 8 2 4 m 6 n Mr. Chin-Sung Lin

ERHS Math Geometry Alternate Exterior Angles 1 and 8 are alternate exterior angles 2 and 7 are alternate exterior angles k 1 3 5 7 8 2 4 m 6 n Mr. Chin-Sung Lin

ERHS Math Geometry Corresponding Angles 1 and 5, 2 and 6, 3 and 7, 4 and 8 are corresponding angles k 1 3 5 7 8 2 4 m 6 n Mr. Chin-Sung Lin

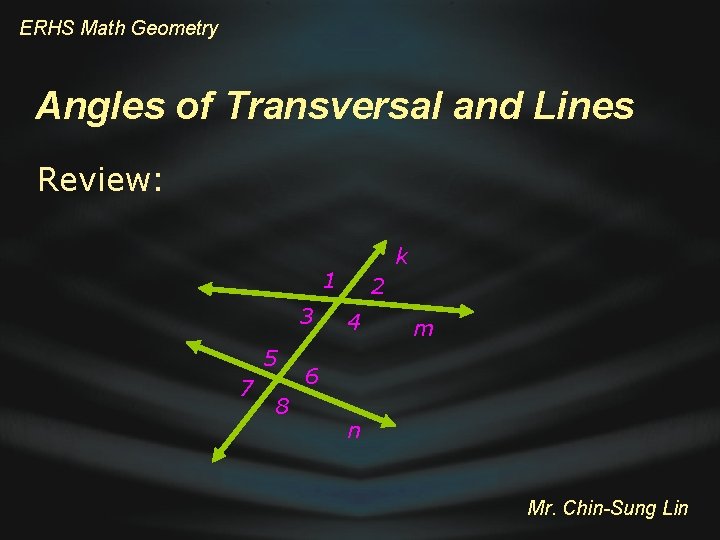
ERHS Math Geometry Angles of Transversal and Lines Review: k 1 3 5 7 8 2 4 m 6 n Mr. Chin-Sung Lin

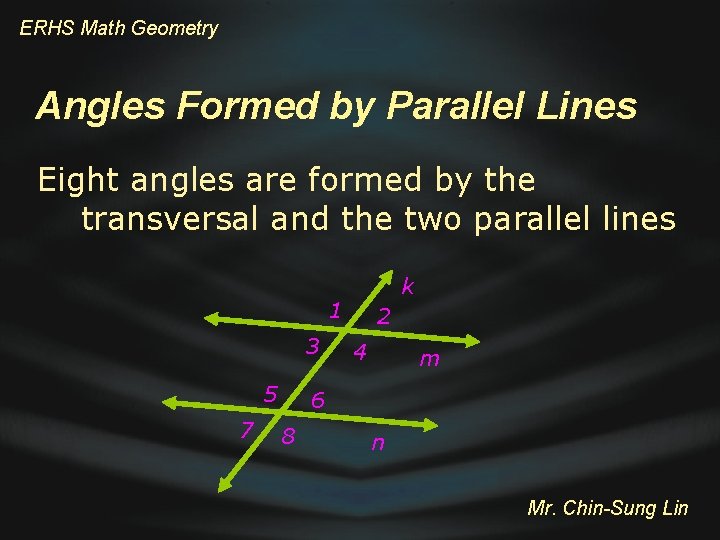
ERHS Math Geometry Angles Formed by Parallel Lines Mr. Chin-Sung Lin

ERHS Math Geometry Parallel Lines Coplanar lines that have no points in common, or have all points in common and, therefore, coincide Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines Eight angles are formed by the transversal and the two parallel lines k 1 3 5 7 2 4 m 6 8 n Mr. Chin-Sung Lin

ERHS Math Geometry Parallel Lines and Transversal q Corresponding Angles Postulate q Alternate Interior Angles Theorem q Same-Side Interior Angles Theorem Mr. Chin-Sung Lin

ERHS Math Geometry Parallel Lines and Transversal q Converse of Corresponding Angles Postulate q Converse of Alternate Interior Angles Theorem q Converse of Same-Side Interior Angles Theorem Mr. Chin-Sung Lin

ERHS Math Geometry Corresponding Angles Postulate If two parallel lines are cut by a transversal, then corresponding angles are congruent If m || n, 1 5, 2 6, 3 7, and 4 8 k 1 3 5 7 2 4 m 6 8 n Mr. Chin-Sung Lin

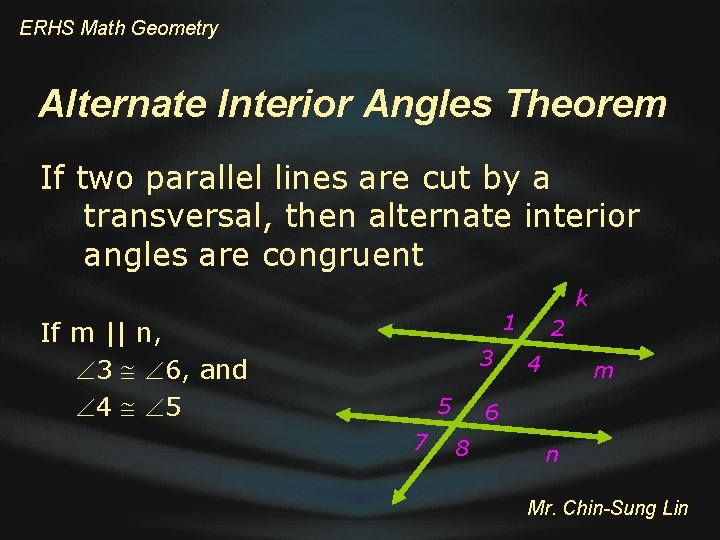
ERHS Math Geometry Alternate Interior Angles Theorem If two parallel lines are cut by a transversal, then alternate interior angles are congruent k 1 If m || n, 3 6, and 4 5 3 5 7 2 4 m 6 8 n Mr. Chin-Sung Lin

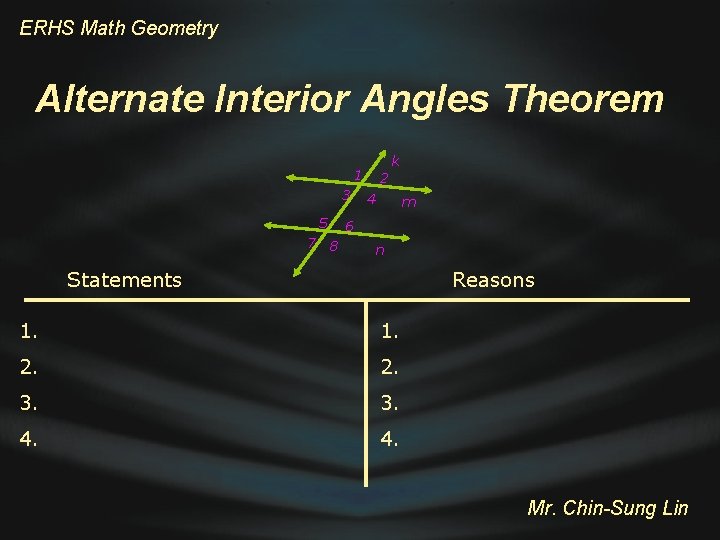
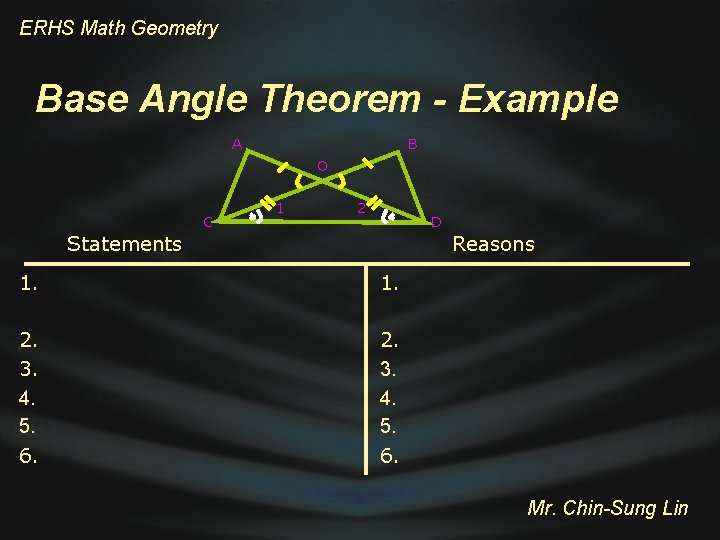
ERHS Math Geometry Alternate Interior Angles Theorem k 1 3 5 7 8 2 4 m 6 n Statements Reasons 1. 2. 3. 4. Mr. Chin-Sung Lin

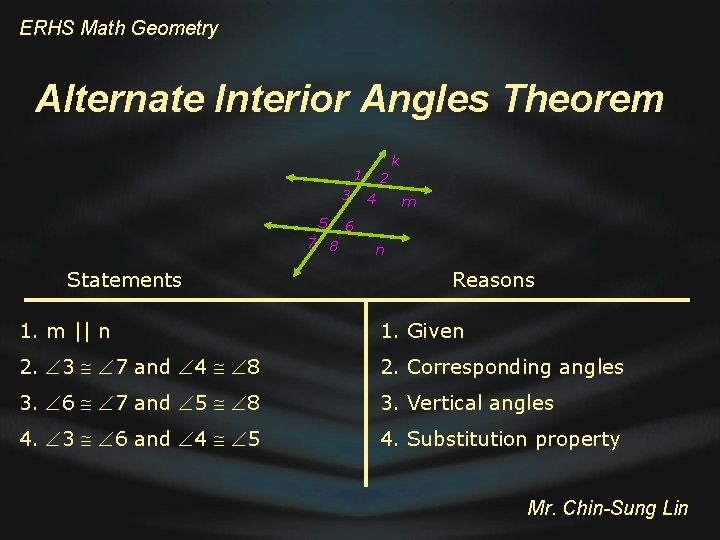
ERHS Math Geometry Alternate Interior Angles Theorem k 1 3 5 7 8 Statements 2 4 m 6 n Reasons 1. m || n 1. Given 2. 3 7 and 4 8 2. Corresponding angles 3. 6 7 and 5 8 3. Vertical angles 4. 3 6 and 4 5 4. Substitution property Mr. Chin-Sung Lin

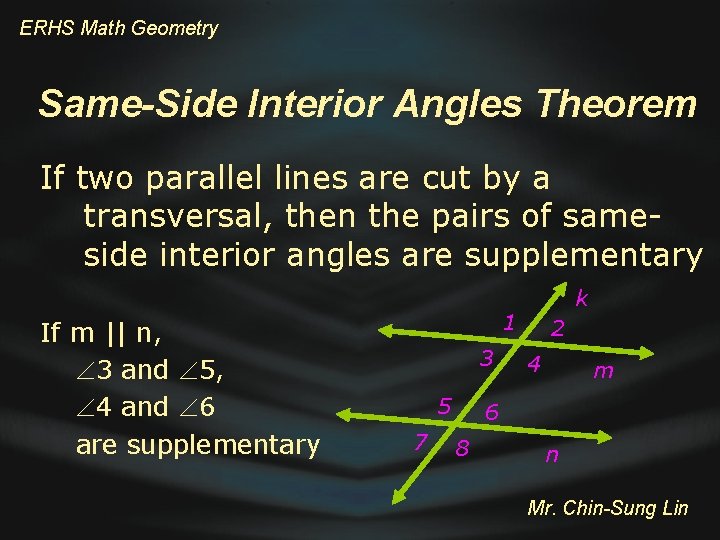
ERHS Math Geometry Same-Side Interior Angles Theorem If two parallel lines are cut by a transversal, then the pairs of sameside interior angles are supplementary If m || n, 3 and 5, 4 and 6 are supplementary k 1 3 5 7 2 4 m 6 8 n Mr. Chin-Sung Lin

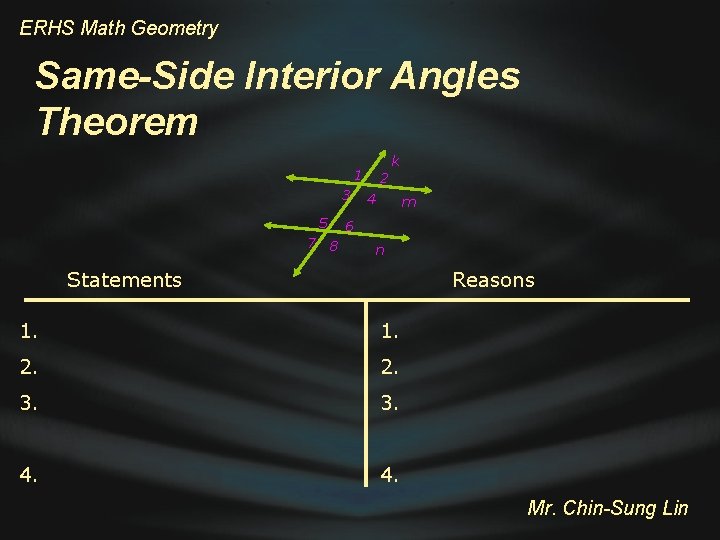
ERHS Math Geometry Same-Side Interior Angles Theorem k 1 3 5 7 8 2 4 m 6 n Statements Reasons 1. 2. 3. 4. Mr. Chin-Sung Lin

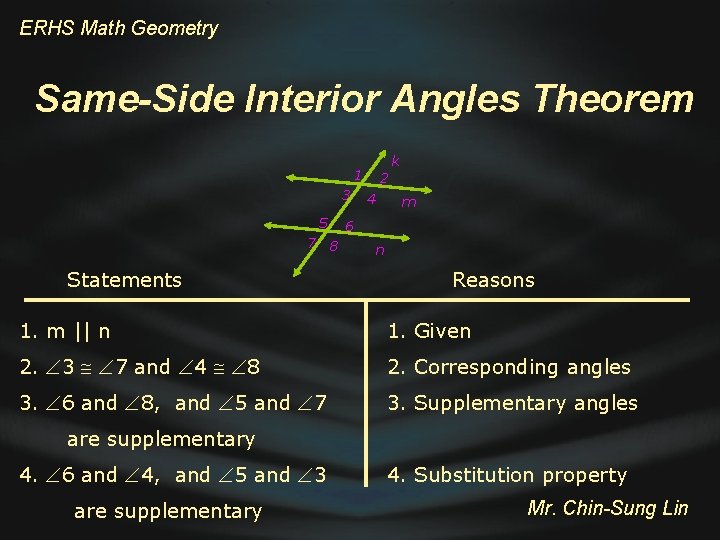
ERHS Math Geometry Same-Side Interior Angles Theorem k 1 3 5 7 8 Statements 2 4 m 6 n Reasons 1. m || n 1. Given 2. 3 7 and 4 8 2. Corresponding angles 3. 6 and 8, and 5 and 7 3. Supplementary angles are supplementary 4. 6 and 4, and 5 and 3 are supplementary 4. Substitution property Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Corresponding Angles Postulate If two lines are cut by a transversal and corresponding angles are congruent, then the lines are parallel If 1 5, 2 6, 3 7 or 4 8, m || n, k 1 3 5 7 2 4 m 6 8 n Mr. Chin-Sung Lin

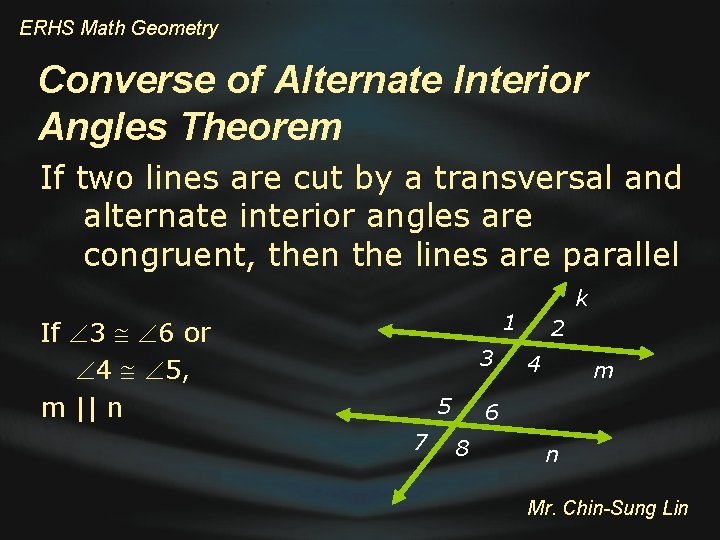
ERHS Math Geometry Converse of Alternate Interior Angles Theorem If two lines are cut by a transversal and alternate interior angles are congruent, then the lines are parallel k 1 If 3 6 or 4 5, m || n 3 5 7 2 4 m 6 8 n Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Alternate Interior Angles Theorem k 1 3 5 7 8 2 4 m 6 n Statements Reasons 1. 2. 3. 4. Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Alternate Interior Angles Theorem k 1 3 5 7 8 Statements 2 4 m 6 n Reasons 1. 3 6 or 4 5 1. Given 2. 6 7 and 5 8 2. Vertical angles 3. 3 7 or 4 8 3. Substitution property 4. m || n 4. Converse of corresponding angle postulate Mr. Chin-Sung Lin

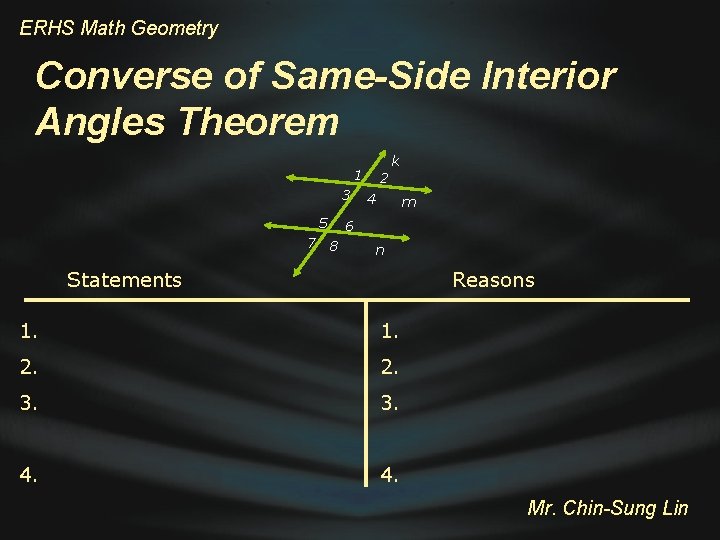
ERHS Math Geometry Converse of Same-Side Interior Angles Theorem If two lines are cut by a transversal and the pairs of same-side interior angles are supplementary, then the lines are parallel k 1 If 3 and 5, or 4 and 6 are supplementary, m || n, 3 5 7 2 4 m 6 8 n Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Same-Side Interior Angles Theorem k 1 3 5 7 8 2 4 m 6 n Statements Reasons 1. 2. 3. 4. Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Same-Side Interior Angles Theorem k 1 3 5 7 8 Statements 1. 4 and 6, or 3 and 5 are supplementary 2. 8 and 6, and 7 and 5 are supplementary 3. 4 8 or 3 7 4. m || n 2 4 m 6 n Reasons 1. Given 2. Supplementary angles 3. Supp. angle theorem 4. Converse of corresponding angle postulate Mr. Chin-Sung Lin

ERHS Math Geometry Methods of Proving Lines Parallel q Congruent Corresponding Angles q Congruent Alternate Interior Angles q Same-Side Interior Angles supplementary q Both lines are perpendicular to the same line Mr. Chin-Sung Lin

ERHS Math Geometry Examples Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines Classify the following angles into alternate interior angles, same-side interior angles or corresponding angles q 4 3 8 7 p 2 1 r 6 5 Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines Alternate interior angles: 3 & 6, 2 & 7 Same-side interior angles: 2 & 3, 6 & 7 Corresponding angles: 1 & 3, 2 & 4, 5 & 7, 6 & 8 q 4 3 8 7 p 2 1 r 6 5 Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines If p and q are parallel, calculate the value of all the angles q r 4 3 125 o 7 p 2 1 6 5 Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines Calculate the value of all the angles q 55 o p r 125 o 55 o Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines If p and q are parallel, calculate the value of x q r 4 3 x+50 o 7 p 2 1 6 x– 10 o Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines If p and q are parallel, calculate the value of x x + 50 o + x – 10 o = 180 o 2 x = 140 o x = 70 o q r 4 3 x+50 o 7 p 2 1 6 x– 10 o Mr. Chin-Sung Lin

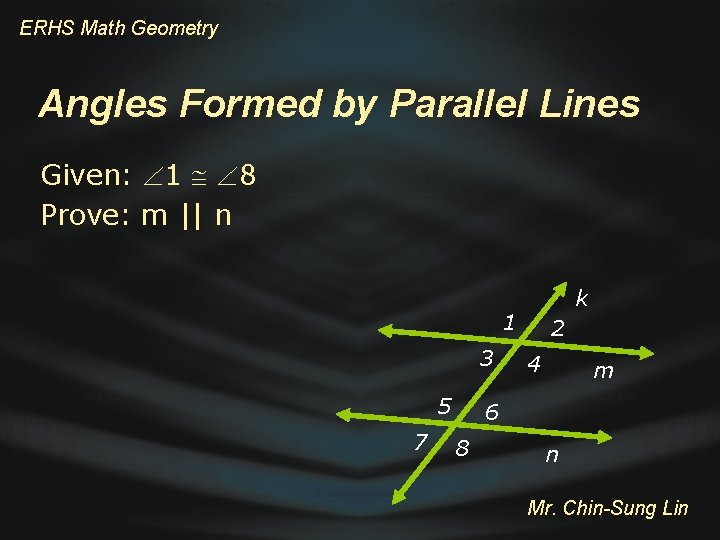
ERHS Math Geometry Angles Formed by Parallel Lines Given: 1 8 Prove: m || n k 1 3 5 7 2 4 m 6 8 n Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines Given: 1 8 Prove: m || n Statements k 1 3 5 2 4 m 6 7 8 n Reasons 1. 1 8 1. Given 2. 1 4 and 8 5 2. Vertical angles 3. 4 5 3. Substitution property 4. m || n 4. Converse of alternate interior angle theorem Mr. Chin-Sung Lin

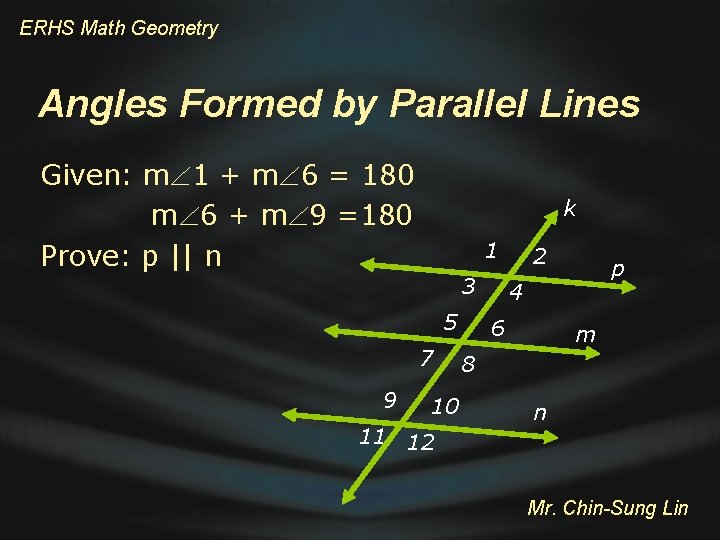
ERHS Math Geometry Angles Formed by Parallel Lines Given: m 1 + m 6 = 180 m 6 + m 9 =180 Prove: p || n k 1 3 5 7 9 10 11 12 2 p 4 6 m 8 n Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines k 1 Given: m 1 + m 6 = 180 m 6 + m 9 =180 Prove: p || n 3 5 7 9 11 Statements 1. m 1 + m 6 180 m 6 + m 9 180 2. 1 4 and 6 7 3. m 4 + m 6 180 m 7 + m 9 180 4. p || m, m || n 5. p || n 10 12 2 p 4 6 m 8 n Reasons 1. Given 2. Vertical angles 3. Substitution property 4. Converse of same-side interior angle theorem 5. Transitive property Mr. Chin-Sung Lin

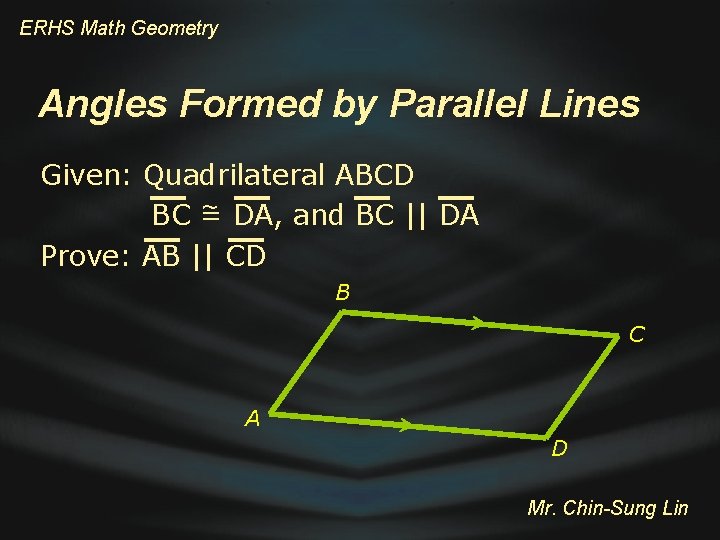
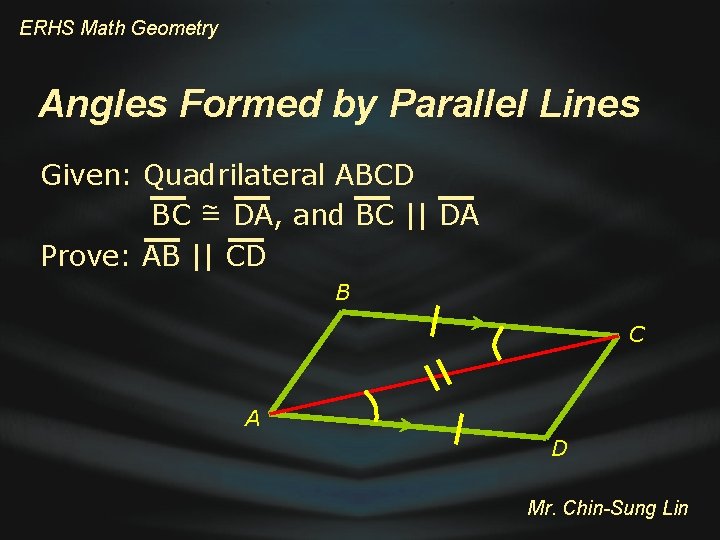
ERHS Math Geometry Angles Formed by Parallel Lines Given: Quadrilateral ABCD ~ DA, and BC || DA BC = Prove: AB || CD B C A D Mr. Chin-Sung Lin

ERHS Math Geometry Angles Formed by Parallel Lines Given: Quadrilateral ABCD ~ DA, and BC || DA BC = Prove: AB || CD B C A D Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Angle-Sum Theorem Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Angle-Sum Theorem The sum of the measures of the interior angles of any triangle is 180 Mr. Chin-Sung Lin

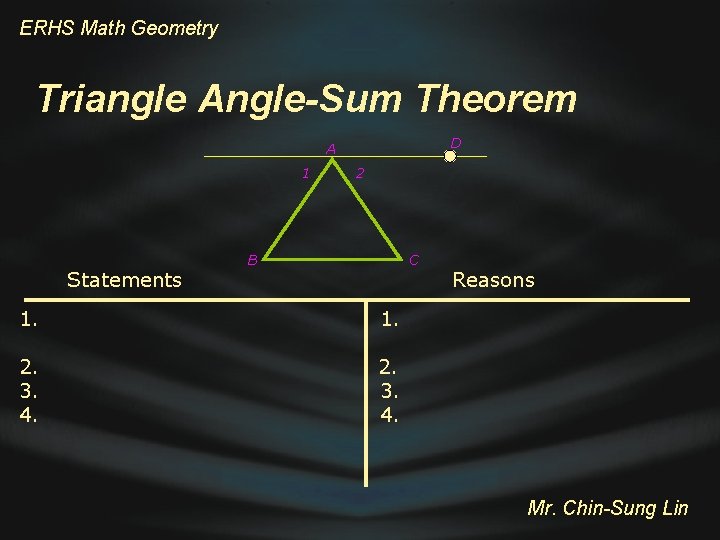
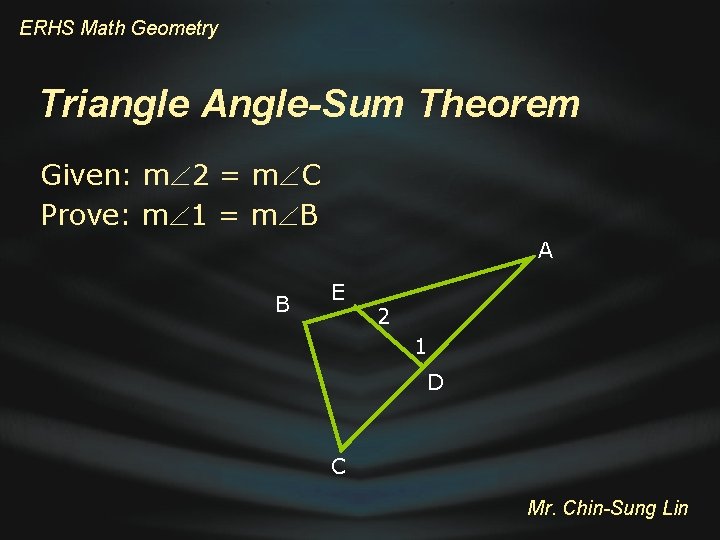
ERHS Math Geometry Triangle Angle-Sum Theorem The sum of the measures of the interior angles of any triangle is 180. A Draw the graph Given: ∆ ABC Prove: m A + m B B+ m C = 180 C Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Angle-Sum Theorem D A 1 Statements 2 B C 1. 2. 3. 4. Reasons Mr. Chin-Sung Lin

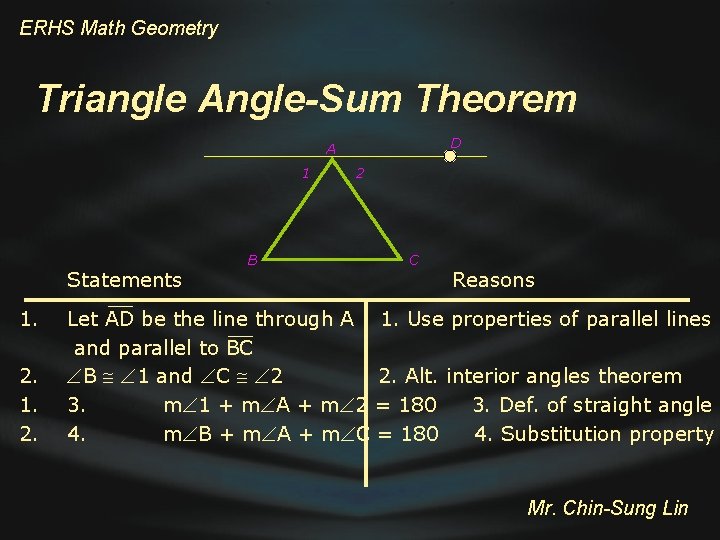
ERHS Math Geometry Triangle Angle-Sum Theorem D A 1 Statements 1. 2. B 2 C Reasons Let AD be the line through A 1. Use properties of parallel lines and parallel to BC B 1 and C 2 2. Alt. interior angles theorem 3. m 1 + m A + m 2 = 180 3. Def. of straight angle 4. m B + m A + m C = 180 4. Substitution property Mr. Chin-Sung Lin

ERHS Math Geometry Corollaries to the Triangle Angle-Sum Theorem Mr. Chin-Sung Lin

ERHS Math Geometry Corollary A corollary is a statement that follows directly from theorem A corollary is a statement that can be easily proved by applying theorem Mr. Chin-Sung Lin

ERHS Math Geometry Corollary 1 If two angles of one triangle are congruent to two angles of another triangle, then the third angles of the triangles are congruent Mr. Chin-Sung Lin

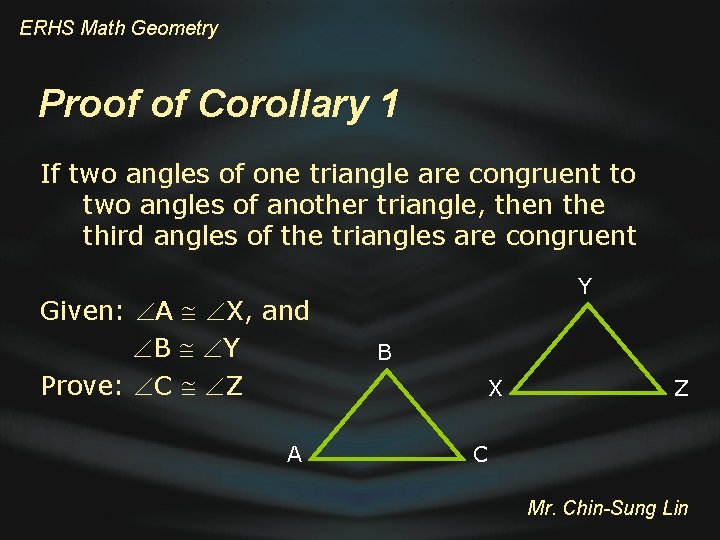
ERHS Math Geometry Proof of Corollary 1 If two angles of one triangle are congruent to two angles of another triangle, then the third angles of the triangles are congruent Given: A X, and B Y Prove: C Z A Y B X Z C Mr. Chin-Sung Lin

ERHS Math Geometry Y Proof of Corollary 1 B X A Statements Z C Reasons 1. A X, B Y 1. Given 2. m A + m B + m C = 180 2. Triangle sum theorem m X + m Y + m Z = 180 3. m A + m B + m C = 3. Substitution property m X + m Y + m Z 4. m C = m Z or C Z 4. Subtraction property Mr. Chin-Sung Lin

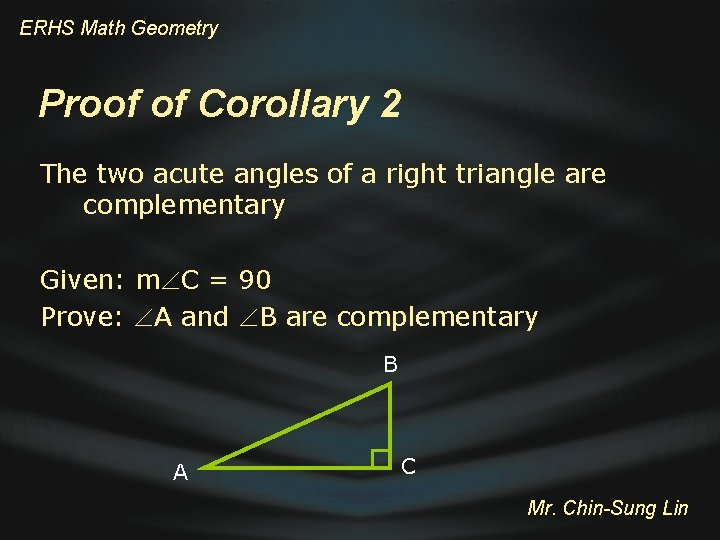
ERHS Math Geometry Corollary 2 The two acute angles of a right triangle are complementary Mr. Chin-Sung Lin

ERHS Math Geometry Proof of Corollary 2 The two acute angles of a right triangle are complementary Given: m C = 90 Prove: A and B are complementary B A C Mr. Chin-Sung Lin

ERHS Math Geometry B Proof of Corollary 2 C A Statements Reasons 1. m C = 90 1. Given 2. m A + m B + m C = 180 2. Triangle sum theorem 3. m A + m B = 180 - 90 = 90 3. Subtraction property 4. A and B are complementary 4. Def. of complementary angles Mr. Chin-Sung Lin

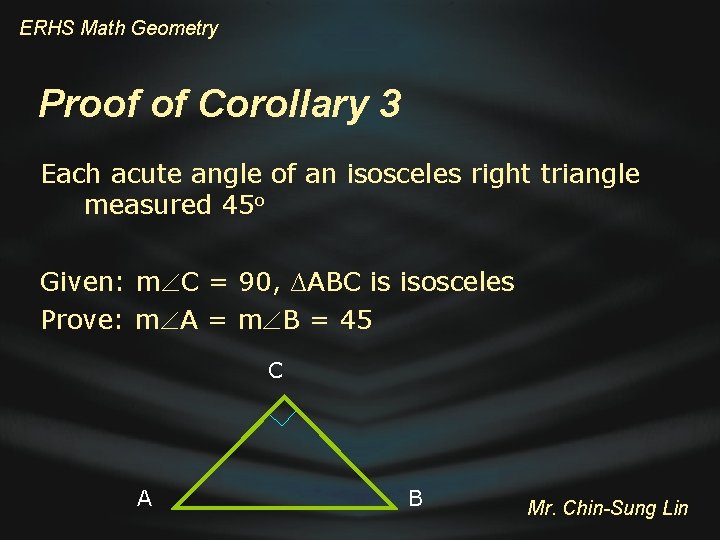
ERHS Math Geometry Corollary 3 Each acute angle of an isosceles right triangle measured 45 o Mr. Chin-Sung Lin

ERHS Math Geometry Proof of Corollary 3 Each acute angle of an isosceles right triangle measured 45 o Given: m C = 90, ∆ABC is isosceles Prove: m A = m B = 45 C A B Mr. Chin-Sung Lin

ERHS Math Geometry C Proof of Corollary 3 A Statements B Reasons 1. m C = 90 1. Given 2. m A + m B + m C = 180 2. Triangle sum theorem 3. m A + m B + 90 = 180 3. Substitution property 4. m A + m B = 90 4. Subtraction property 5. m A = m B 5. Base angle theorem 6. 2 m A = 2 m B = 90 6. Substitution property 7. m A = m B = 45 7. Division property Mr. Chin-Sung Lin

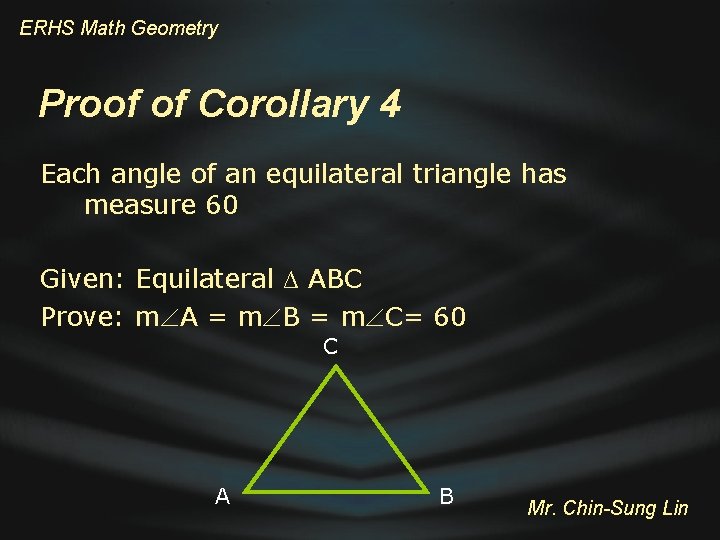
ERHS Math Geometry Corollary 4 Each angle of an equilateral triangle has measure 60 Mr. Chin-Sung Lin

ERHS Math Geometry Proof of Corollary 4 Each angle of an equilateral triangle has measure 60 Given: Equilateral ∆ ABC Prove: m A = m B = m C= 60 C A B Mr. Chin-Sung Lin

ERHS Math Geometry C Proof of Corollary 4 A Statements B Reasons 1. Equilateral ∆ ABC 1. Given 2. m A = m B = m C 2. Euailateral triangle theorem 3. m A + m B + m C = 180 3. Triangle sum theorem 4. m A + m A = 180 4. Substitution property m B + m B = 180 m C + m C = 180 5. m A = m B = m C = 60 5. Division property Mr. Chin-Sung Lin

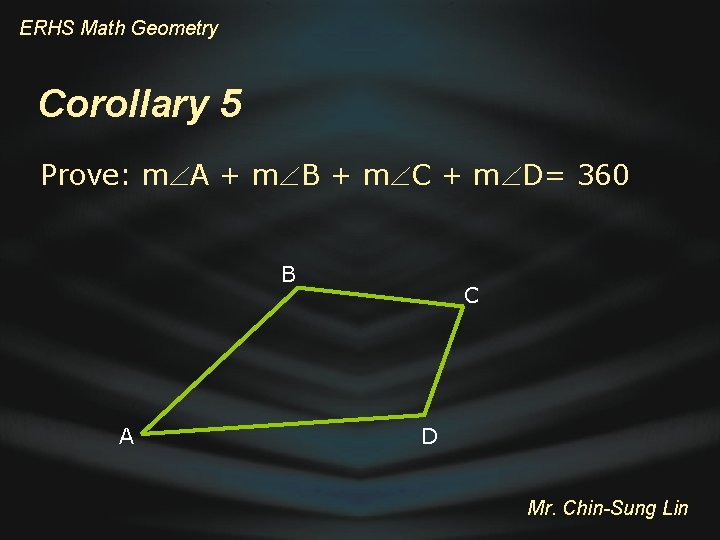
ERHS Math Geometry Corollary 5 Prove: m A + m B + m C + m D= 360 B A C D Mr. Chin-Sung Lin

ERHS Math Geometry Proof of Corollary 5 B 3 1 A 2 Statements 1. Let AC divides quadrilateral ABCD into two triangles 2. m 1 + m B + m 3 = 180 m 2 + m D + m 4 = 180 3. m 1 + m B + m 3 + m 2 + m D + m 4 = 360 4. m A + m B + m C + m D = 360 C 4 D Reasons 1. Use properties of triangles 2. Triangle-sum theorem 3. Addition property 4. Partition property Mr. Chin-Sung Lin

ERHS Math Geometry Exterior Angle Theorem Mr. Chin-Sung Lin

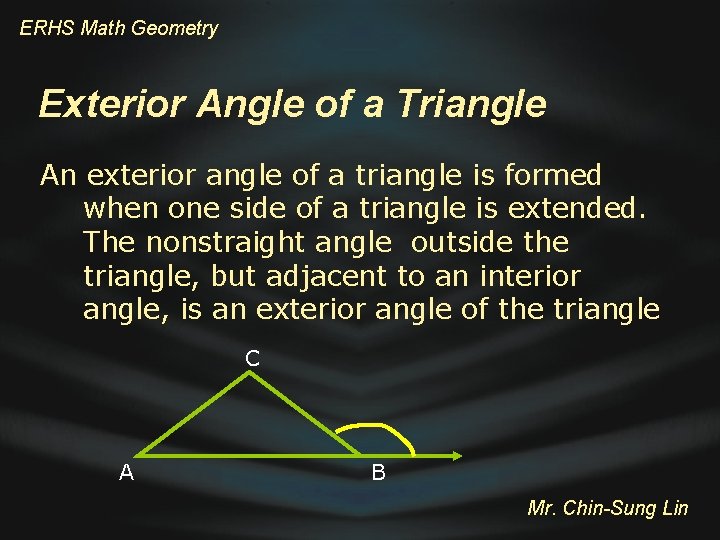
ERHS Math Geometry Exterior Angle of a Triangle An exterior angle of a triangle is formed when one side of a triangle is extended. The nonstraight angle outside the triangle, but adjacent to an interior angle, is an exterior angle of the triangle C A B Mr. Chin-Sung Lin

ERHS Math Geometry Exterior Angle Theorem The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles Mr. Chin-Sung Lin

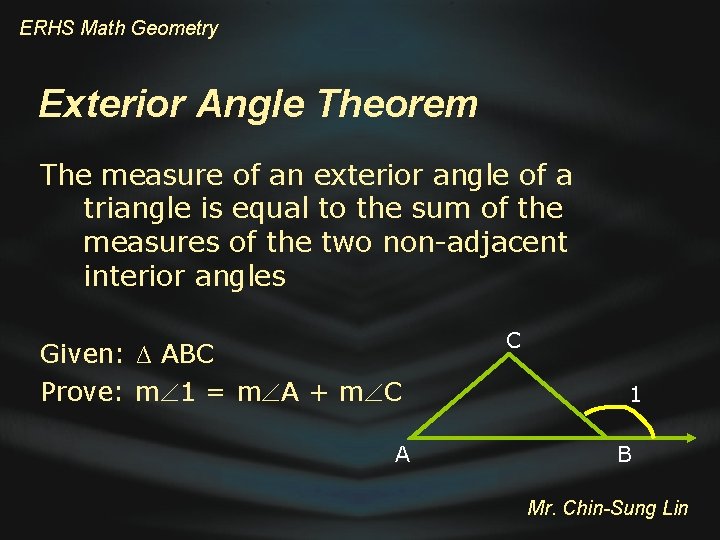
ERHS Math Geometry Exterior Angle Theorem The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles Given: ∆ ABC Prove: m 1 = m A + m C A C 1 B Mr. Chin-Sung Lin

ERHS Math Geometry C Exterior Angle Theorem 1 A Statements B Reasons 1. m 1 + m B = 180 1. Supplementary angles 2. m A + m B + m C = 180 2. Triangle-sum theorem 3. m A + m B + m C = 3. Substitution property m 1 + m B 4. m 1 = m A + m C 4. Subtraction property Mr. Chin-Sung Lin

ERHS Math Geometry Application Examples Mr. Chin-Sung Lin

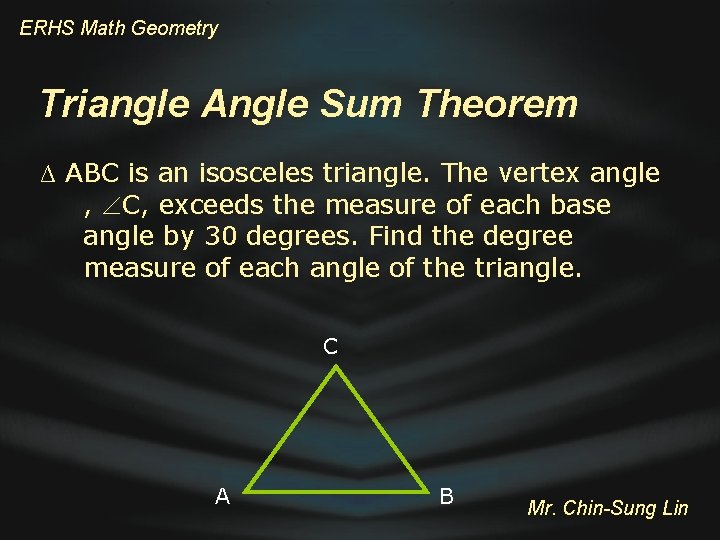
ERHS Math Geometry Triangle Angle Sum Theorem ∆ ABC is an isosceles triangle. The vertex angle , C, exceeds the measure of each base angle by 30 degrees. Find the degree measure of each angle of the triangle. C A B Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Angle Sum Theorem ∆ ABC is an isosceles triangle. The vertex angle , C, exceeds the measure of each base angle by 30 degrees. Find the degree measure of each angle of the triangle C (x + 30) + x = 180 3 x + 30 = 180 3 x = 150 A x = 50 X+30 X X B Mr. Chin-Sung Lin

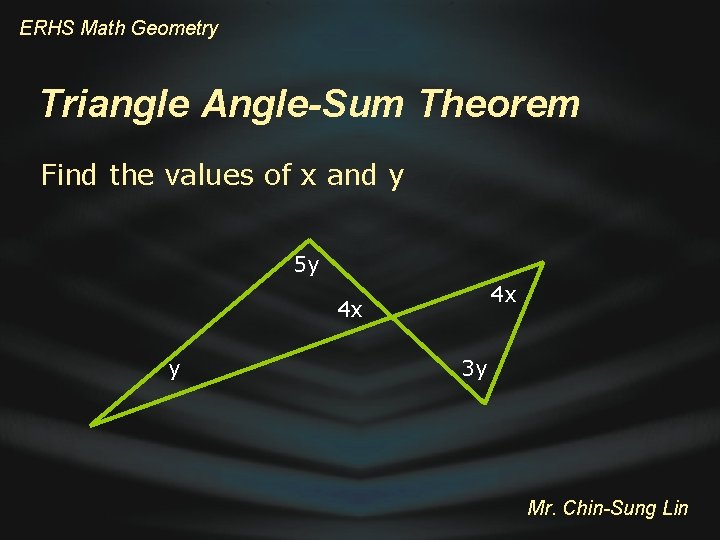
ERHS Math Geometry Triangle Angle-Sum Theorem Find the values of x and y 5 y 4 x 4 x y 3 y Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Angle-Sum Theorem Find the values of x and y 5 y 5 y + 4 x = 180 4 x + 3 y = 180 4 x + 6 y = 180……(1) 8 x + 3 y = 180……(2) (1)/2, 2 x + 3 y = 90. . …. . (3) (2) - (3), 6 x = 90, and then X = 15……(4) Substitutes into (3), 2(15) + 3 y = 90, 3 y = 60, y = 20 4 x y 4 x 3 y So, X =15 Y = 20 Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Angle-Sum Theorem Given: m 2 = m C Prove: m 1 = m B A B E 2 1 D C Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Angle-Sum Theorem A B Statements E 2 C 1. m 2 = m C 2. m 1 + m 2 + m A = 180 m B + m C + m A = 180 3. m 1 + m 2 + m A = m B + m C + m A 4. m 1 + m C + m A = m B + m C + m A 5. m 1 = m B 1 D Reasons 1. Given 2. Triangle-sum theorem 3. Substitution property 4. Substitution property 5. Subtraction property Mr. Chin-Sung Lin

ERHS Math Geometry AAS Postulate Mr. Chin-Sung Lin

ERHS Math Geometry Postulates that Prove Congruent Triangles Side-Side Congruence (SSS) Side-Angle-Side Congruence (SAS) Angle-Side-Angle Congruence (ASA) Mr. Chin-Sung Lin

ERHS Math Geometry Postulates that Prove Congruent Triangles Side-Side Congruence (SSS) Side-Angle-Side Congruence (SAS) Angle-Side-Angle Congruence (ASA) Angle-Side Congruence (AAS) Mr. Chin-Sung Lin

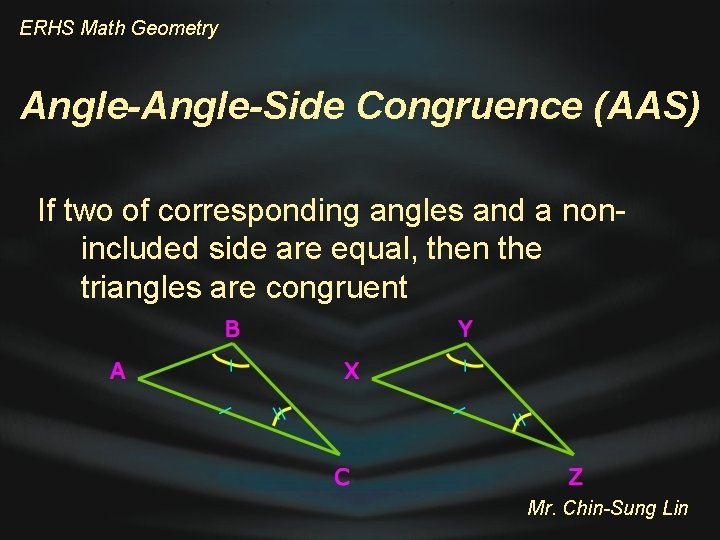
ERHS Math Geometry Angle-Side Congruence (AAS) If two of corresponding angles and a nonincluded side are equal, then the triangles are congruent Mr. Chin-Sung Lin

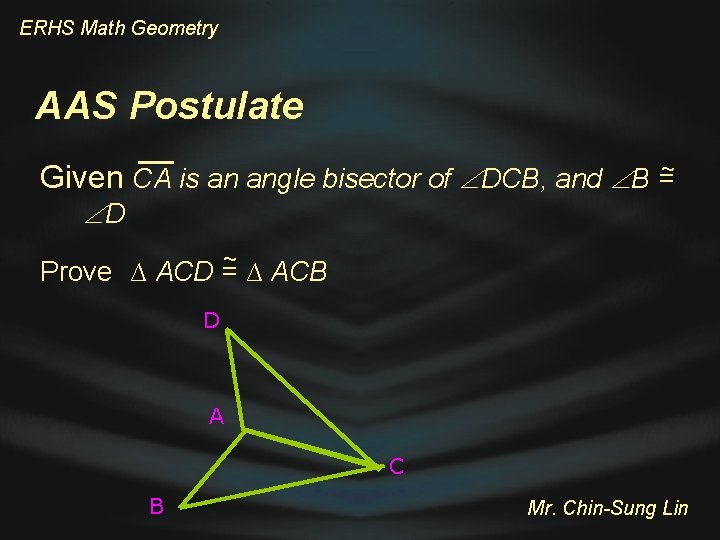
ERHS Math Geometry AAS Postulate Given CA is an angle bisector of DCB, and B =~ D ~ Prove ∆ ACD = ∆ ACB D A C B Mr. Chin-Sung Lin

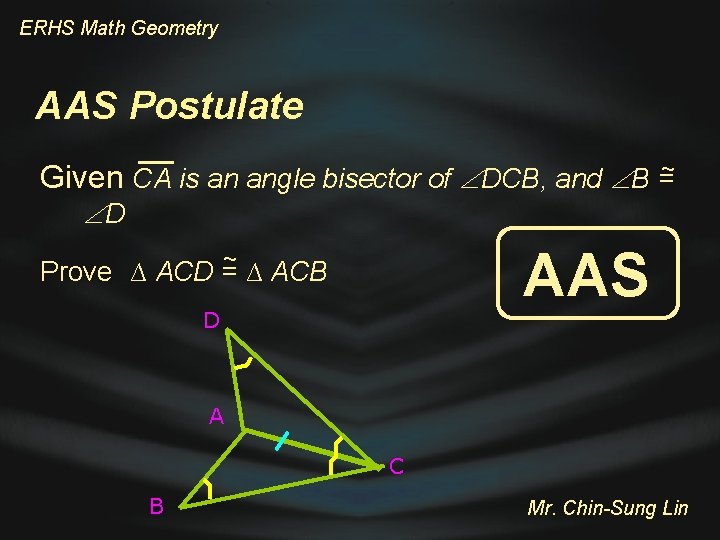
ERHS Math Geometry AAS Postulate Given CA is an angle bisector of DCB, and B =~ D AAS ~ Prove ∆ ACD = ∆ ACB D A C B Mr. Chin-Sung Lin

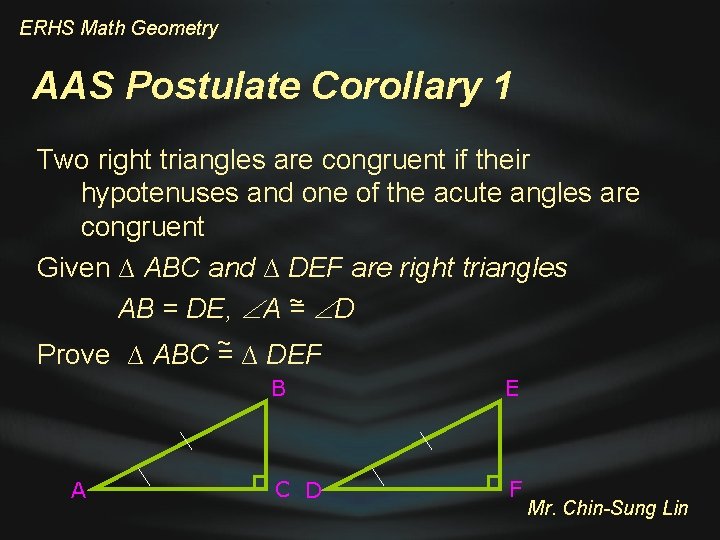
ERHS Math Geometry AAS Postulate Corollary 1 Two right triangles are congruent if their hypotenuses and one of the acute angles are congruent Given ∆ ABC and ∆ DEF are right triangles ~ D AB = DE, A = ~ Prove ∆ ABC = ∆ DEF A B E C D F Mr. Chin-Sung Lin

ERHS Math Geometry AAS Postulate Corollary 2 If a point lies on the bisector of an angle, then it is equidistant from the sides of the angle Mr. Chin-Sung Lin

ERHS Math Geometry Congruent Right Triangles (HL Postulate) Mr. Chin-Sung Lin

ERHS Math Geometry Postulates that Prove Congruent Triangles Side-Side Congruence (SSS) Side-Angle-Side Congruence (SAS) Angle-Side-Angle Congruence (ASA) Angle-Side Congruence (AAS) Mr. Chin-Sung Lin

ERHS Math Geometry Postulates that Prove Congruent Triangles Side-Side Congruence (SSS) Side-Angle-Side Congruence (SAS) Angle-Side-Angle Congruence (ASA) Angle-Side Congruence (AAS) Hypotenuse-Leg Postulate (HL) Mr. Chin-Sung Lin

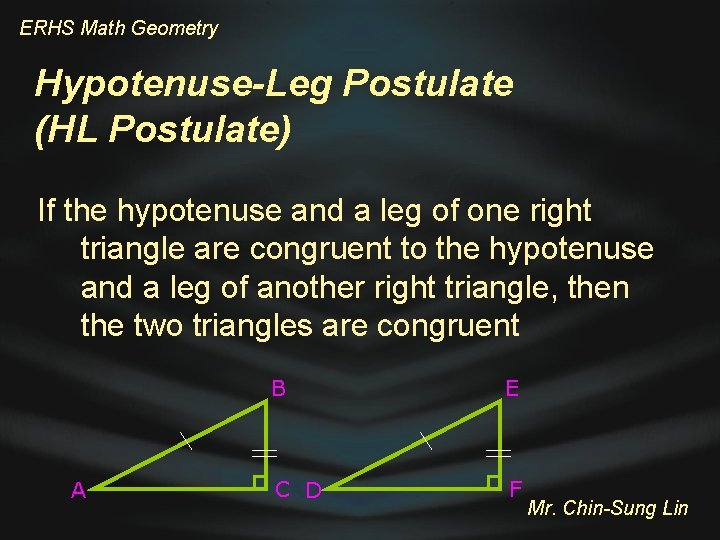
ERHS Math Geometry Hypotenuse-Leg Postulate (HL Postulate) If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the two triangles are congruent A B E C D F Mr. Chin-Sung Lin

ERHS Math Geometry Side-Angle Case (SSA) The condition does not guarantee congruence, because it is possible to have two incongruent triangles. This is known as the ambiguous case Mr. Chin-Sung Lin

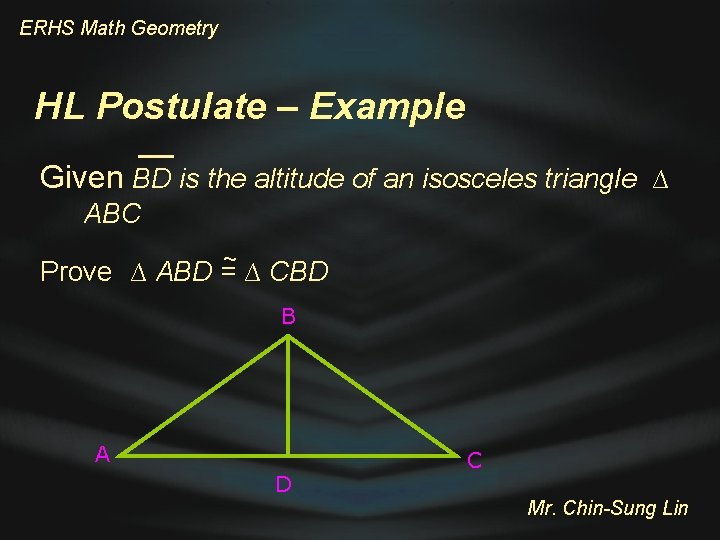
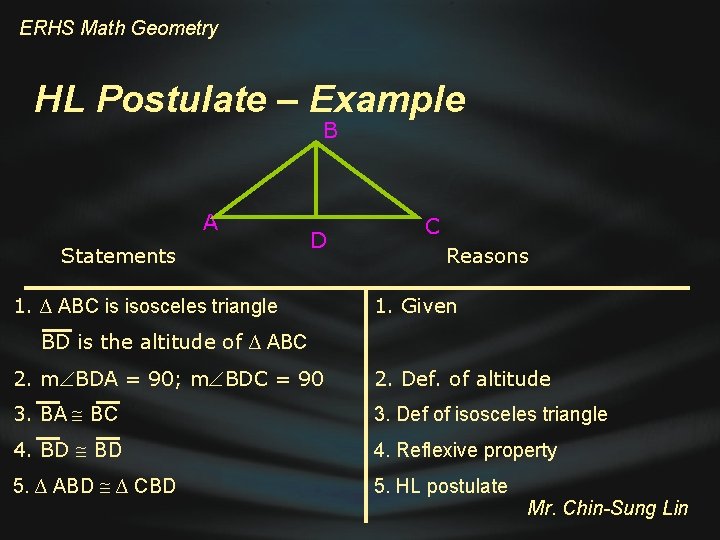
ERHS Math Geometry HL Postulate – Example Given BD is the altitude of an isosceles triangle ∆ ABC ~ Prove ∆ ABD = ∆ CBD B A D C Mr. Chin-Sung Lin

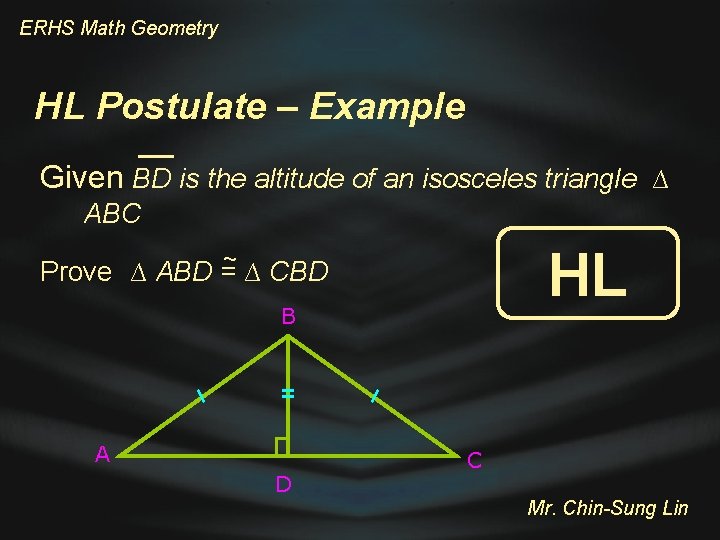
ERHS Math Geometry HL Postulate – Example Given BD is the altitude of an isosceles triangle ∆ ABC HL ~ Prove ∆ ABD = ∆ CBD B A D C Mr. Chin-Sung Lin

ERHS Math Geometry HL Postulate – Example B A Statements D 1. ∆ ABC is isosceles triangle C Reasons 1. Given BD is the altitude of ∆ ABC 2. m BDA = 90; m BDC = 90 2. Def. of altitude 3. BA BC 3. Def of isosceles triangle 4. BD 4. Reflexive property 5. ∆ ABD ∆ CBD 5. HL postulate Mr. Chin-Sung Lin

ERHS Math Geometry Base Angle Theorem Mr. Chin-Sung Lin

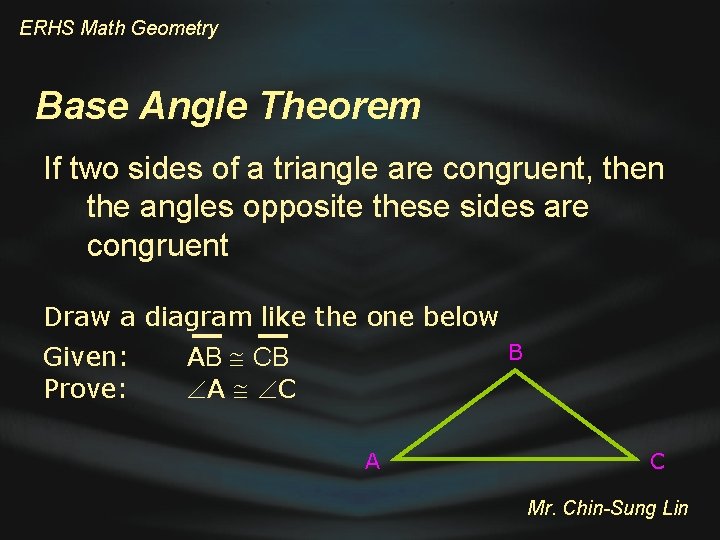
ERHS Math Geometry Base Angle Theorem If two sides of a triangle are congruent, then the angles opposite these sides are congruent (Base angles of an isosceles triangle are congruent) Mr. Chin-Sung Lin

ERHS Math Geometry Base Angle Theorem If two sides of a triangle are congruent, then the angles opposite these sides are congruent Draw a diagram like the one below Given: Prove: B AB CB A C A C Mr. Chin-Sung Lin

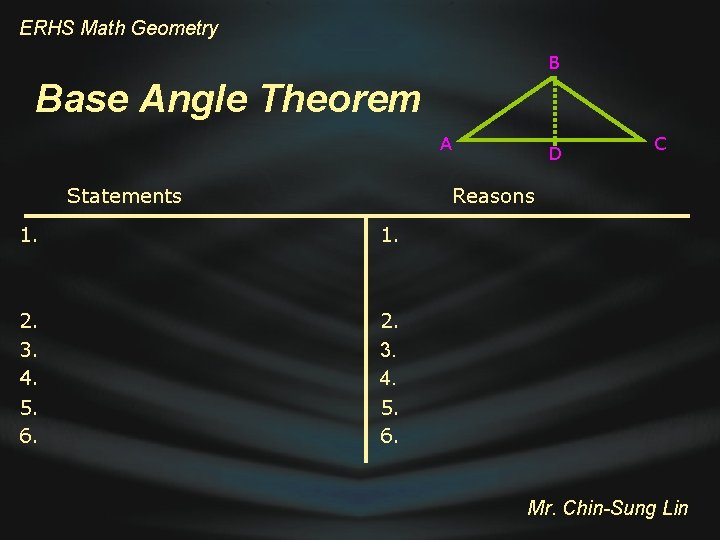
ERHS Math Geometry B Base Angle Theorem A Statements D C Reasons 1. 2. 3. 4. 5. 6. Mr. Chin-Sung Lin

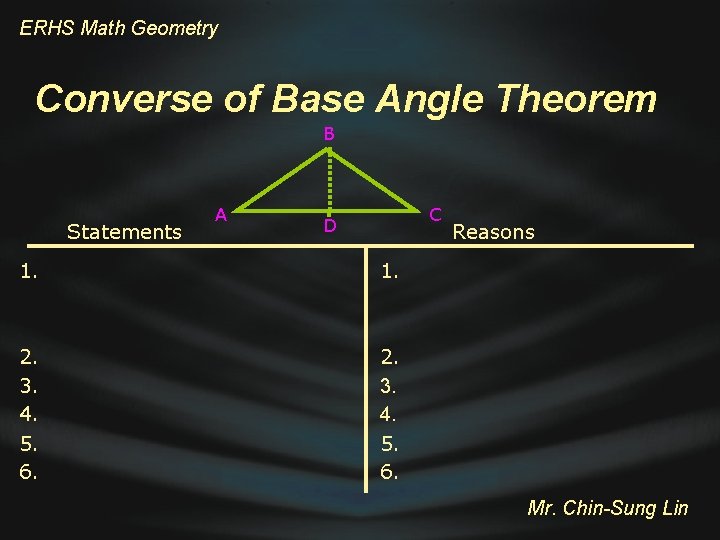
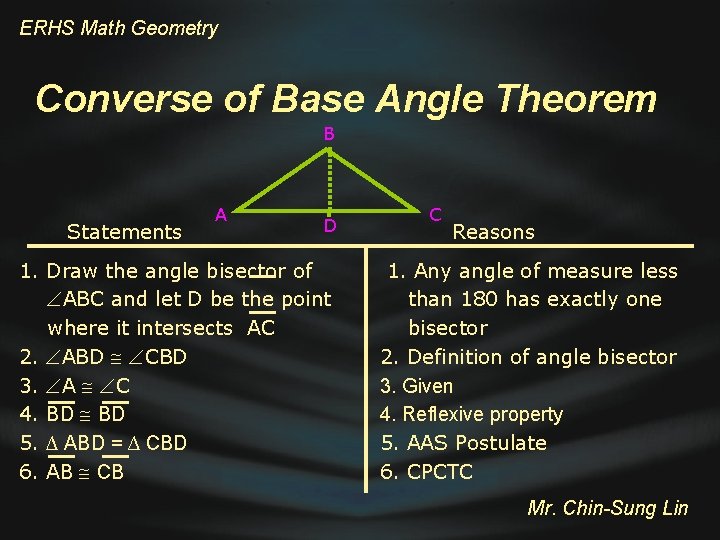
ERHS Math Geometry B Base Angle Theorem A Statements 1. Draw the angle bisector of ABC and let D be the point where it intersects AC 2. ABD CBD 3. AB CB 4. BD 5. ∆ ABD = ∆ CBD 6. A C D C Reasons 1. Any angle of measure less than 180 has exactly one bisector 2. Definition of angle bisector 3. Given 4. Reflexive property 5. SAS Postulate 6. CPCTC Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Base Angle Theorem Mr. Chin-Sung Lin

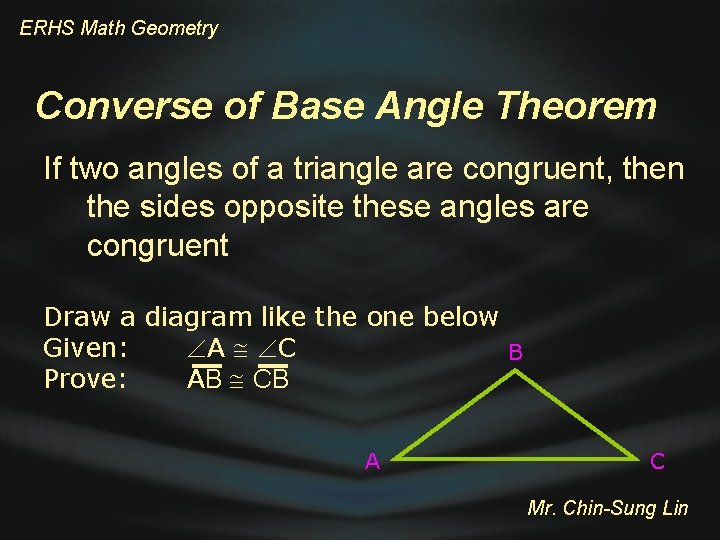
ERHS Math Geometry Converse of Base Angle Theorem If two angles of a triangle are congruent, then the sides opposite these angles are congruent Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Base Angle Theorem If two angles of a triangle are congruent, then the sides opposite these angles are congruent Draw a diagram like the one below Given: A C B Prove: AB CB A C Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Base Angle Theorem B Statements A C D 1. 2. 3. 4. 5. 6. Reasons Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Base Angle Theorem B Statements A D 1. Draw the angle bisector of ABC and let D be the point where it intersects AC 2. ABD CBD 3. A C 4. BD 5. ∆ ABD = ∆ CBD 6. AB CB C Reasons 1. Any angle of measure less than 180 has exactly one bisector 2. Definition of angle bisector 3. Given 4. Reflexive property 5. AAS Postulate 6. CPCTC Mr. Chin-Sung Lin

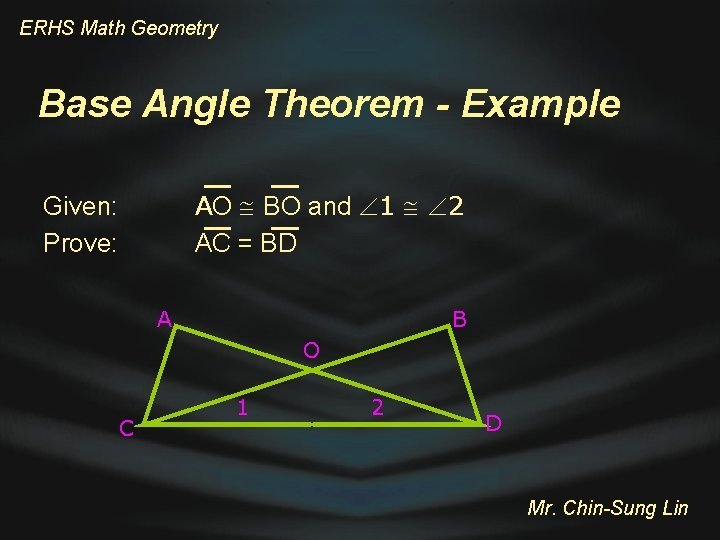
ERHS Math Geometry Base Angle Theorem - Example AO BO and 1 2 AC = BD Given: Prove: A B O C 1 2 D Mr. Chin-Sung Lin

ERHS Math Geometry Base Angle Theorem – Example AO BO and 1 2 AC = BD Given: Prove: A B O C 1 2 D Mr. Chin-Sung Lin

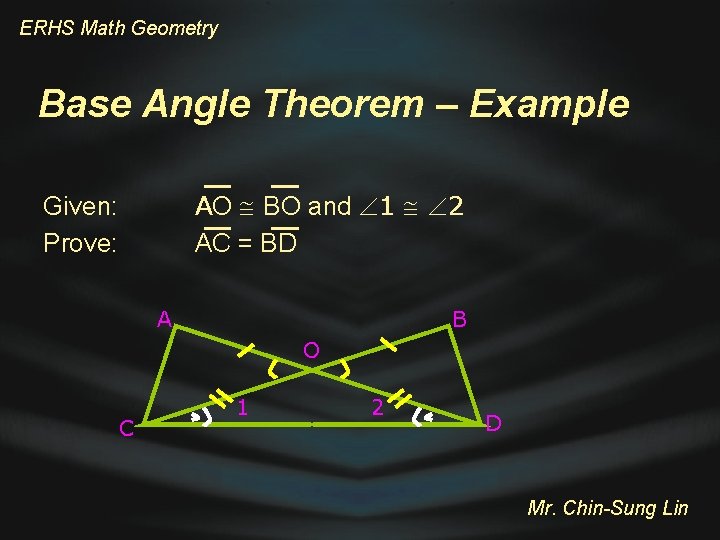
ERHS Math Geometry Base Angle Theorem - Example A B O C 1 2 D Statements Reasons 1. 2. 3. 4. 5. 6. Mr. Chin-Sung Lin

ERHS Math Geometry Base Angle Theorem - Example A B O C Statements 1. 1 2 2. CO DO 3. AO BO 4. AOC BOD 5. ∆ AOC = ∆ BOD 6. AC BD 1 2 D Reasons 1. Given 2. Converse of Base Angle Theorem 3. Given 4. Vertical Angles 5. SAS Postulate 6. CPCTC Mr. Chin-Sung Lin

ERHS Math Geometry Equilateral and Equiangular Triangles Mr. Chin-Sung Lin

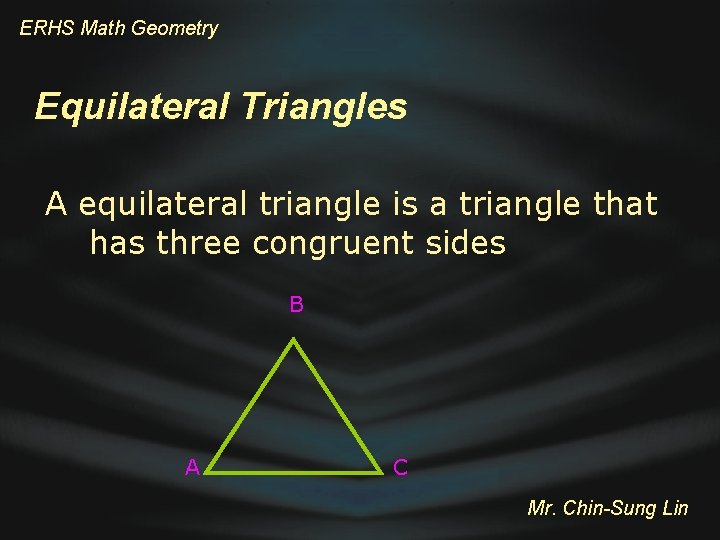
ERHS Math Geometry Equilateral Triangles A equilateral triangle is a triangle that has three congruent sides B A C Mr. Chin-Sung Lin

ERHS Math Geometry Equilateral & Equiangular Triangles If a triangle is an equilateral triangle, then it is an equiangular triangle Mr. Chin-Sung Lin

ERHS Math Geometry Polygons Mr. Chin-Sung Lin

ERHS Math Geometry Definition of Polygons A polygon is a closed plane figure with the following properties: 1. Formed by three or more line segments called sides 2. Each side intersects exactly two sides, one at each endpoint, so that no two sides with a common end point are colinear Mr. Chin-Sung Lin

ERHS Math Geometry Naming Polygons Each endpoint of a side is a vertex of the polygon A polygon can be named by listing the vertices in consecutive order Polygon can be named as ABCDE, CDEAB, EABCD, or …… A B E D C Mr. Chin-Sung Lin

ERHS Math Geometry Convex & Concave Polygons A polygon is convex if no line that contains a side of the polygon contains a point in the interior of the polygon A polygon that is not convex is called nonconvex or concave Interior Convex Concave Mr. Chin-Sung Lin

ERHS Math Geometry Convex & Concave Polygons A polygon is convex if each of the interior angles measures less than 180 degrees A polygon that is concave if at least one interior angle measures more than 180 degrees < 1800 Convex > 1800 Concave Mr. Chin-Sung Lin

ERHS Math Geometry Identifying Polygons Identify polygons in the following figures and tell whether the figure is a convex or concave polygon Mr. Chin-Sung Lin

ERHS Math Geometry Identifying Polygons Identify polygons in the following figures and tell whether the figure is a convex or concave polygon Concave Convex Concave Mr. Chin-Sung Lin

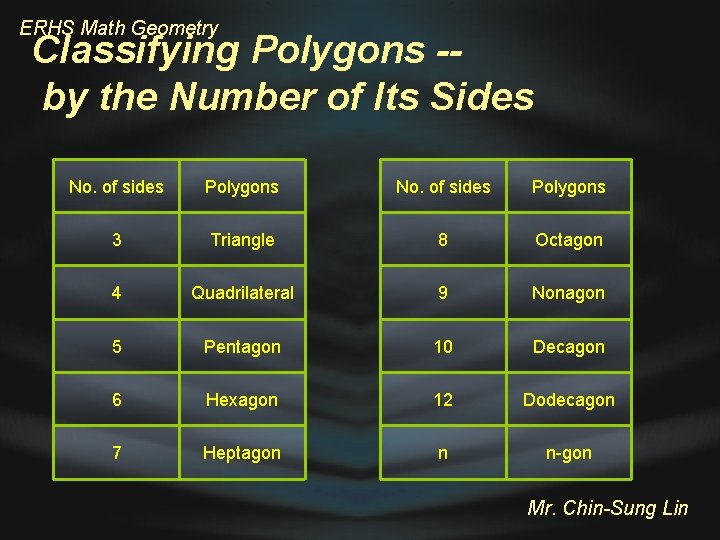
ERHS Math Geometry Common Polygons • Triangle: a polygon that is the union of three line segments • Quadrilateral: a polygon that is the union of four line segments • Pentagon: a polygon that is the union of five line segments • Hexagon: a polygon that is the union of six line segments • Octagon: a polygon that is the union of eight line segments • Decagon: a polygon that is the union of ten line segments • N-gon: a polygon with n sides Mr. Chin-Sung Lin

ERHS Math Geometry Classifying Polygons -by the Number of Its Sides No. of sides Polygons 3 Triangle 8 Octagon 4 Quadrilateral 9 Nonagon 5 Pentagon 10 Decagon 6 Hexagon 12 Dodecagon 7 Heptagon n n-gon Mr. Chin-Sung Lin

ERHS Math Geometry Classifying Polygons -by the Number of Its Sides Mr. Chin-Sung Lin

ERHS Math Geometry Classifying Polygons -by the Number of Its Sides Pentagon Hexagon Quadrilateral Triangle Mr. Chin-Sung Lin

ERHS Math Geometry Classifying Polygons -by the Number of Its Sides Mr. Chin-Sung Lin

ERHS Math Geometry Classifying Polygons -by the Number of Its Sides Decagon Heptagon Dodecagon 16 -gon Mr. Chin-Sung Lin

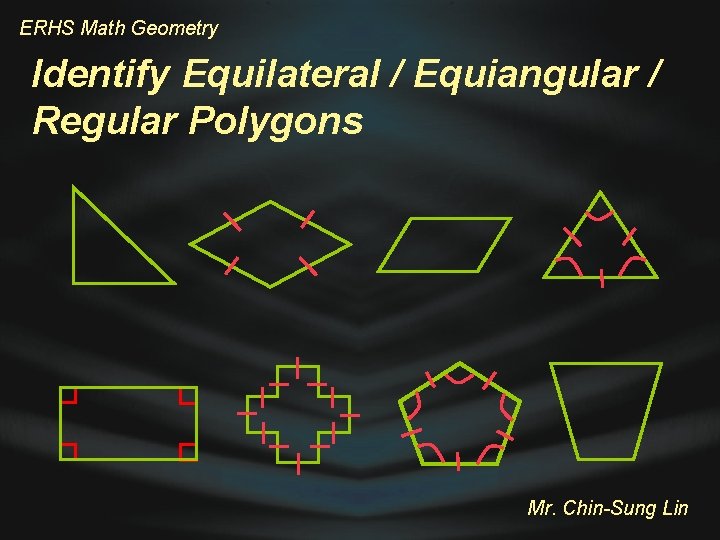
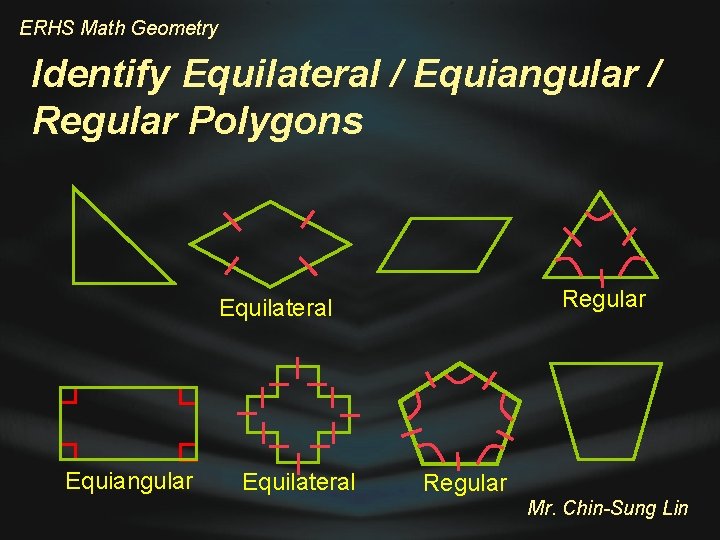
ERHS Math Geometry Equilateral / Equiangular / Regular Polygons A polygon is equilateral if all sides are congruent A polygon is equiangular if all interior angles of the polygon are congruent A regular polygon is a convex polygon that is both equilateral and equiangular Equilateral Equiangular Regular Mr. Chin-Sung Lin

ERHS Math Geometry Identify Equilateral / Equiangular / Regular Polygons Mr. Chin-Sung Lin

ERHS Math Geometry Identify Equilateral / Equiangular / Regular Polygons Regular Equilateral Equiangular Equilateral Regular Mr. Chin-Sung Lin

ERHS Math Geometry Interior and Exterior Angles of Polygons Mr. Chin-Sung Lin

ERHS Math Geometry Consecutive Angles and Vertices A pair of angles whose vertices are the endpoints of a common side are called consecutive angles The verteices of consecutive angles are called consecutive vertices or adjacent vertices A E B Consecutive Angles: A and B Consecutive Angles: C and D Consecutive Vertices: A and B Non-adjacent Vertices: E and B D C Mr. Chin-Sung Lin

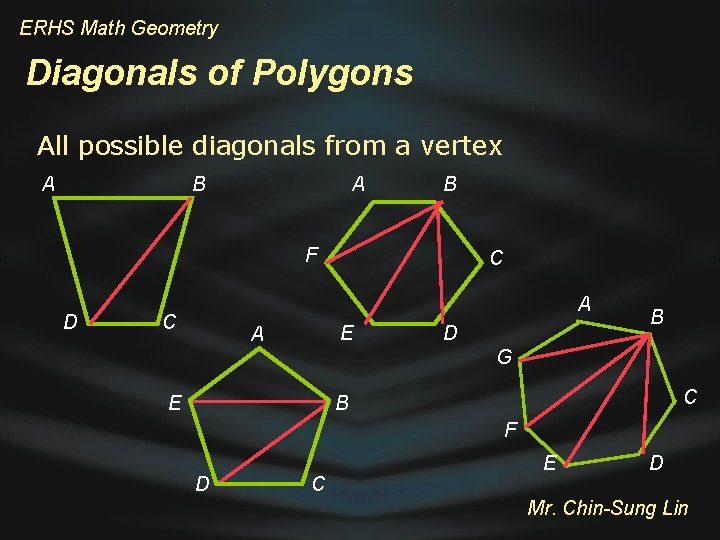
ERHS Math Geometry Diagonals of Polygons A diagonal of a polygon is a line segment whose endpoints are two non-adjacent vertices A Adjacent Vertices of B: A and C E B Non-adjacent Vertices of B: D and E Diagonals with Endpoint B: BD and BE D C Mr. Chin-Sung Lin

ERHS Math Geometry Diagonals of Polygons A diagonal of a polygon is a line segment whose endpoints are two non-adjacent vertices A Adjacent Vertices of B: A and C E B Non-adjacent Vertices of B: D and E Diagonals with Endpoint B: BD and BE D C Mr. Chin-Sung Lin

ERHS Math Geometry Diagonals of Polygons All possible diagonals from a vertex A B F D C A C E A D B G E C B F D C E D Mr. Chin-Sung Lin

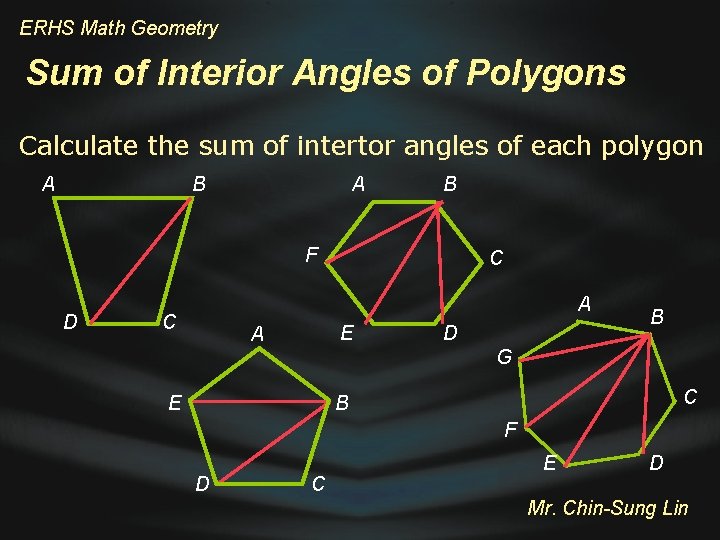
ERHS Math Geometry Sum of Interior Angles of Polygons Calculate the sum of intertor angles of each polygon A B F D C A C E A D B G E C B F D C E D Mr. Chin-Sung Lin

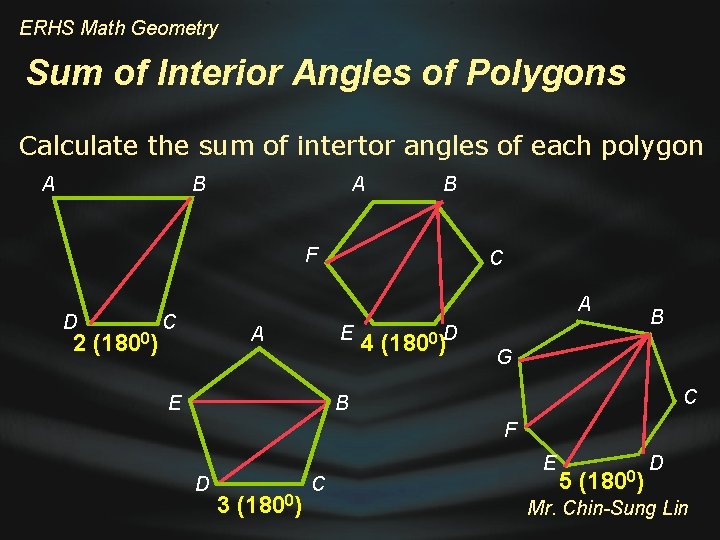
ERHS Math Geometry Sum of Interior Angles of Polygons Calculate the sum of intertor angles of each polygon A B F D 2 (1800) C A C E A E 0 D 4 (180 ) B G C B F D 3 (1800) C E 5 (1800) D Mr. Chin-Sung Lin

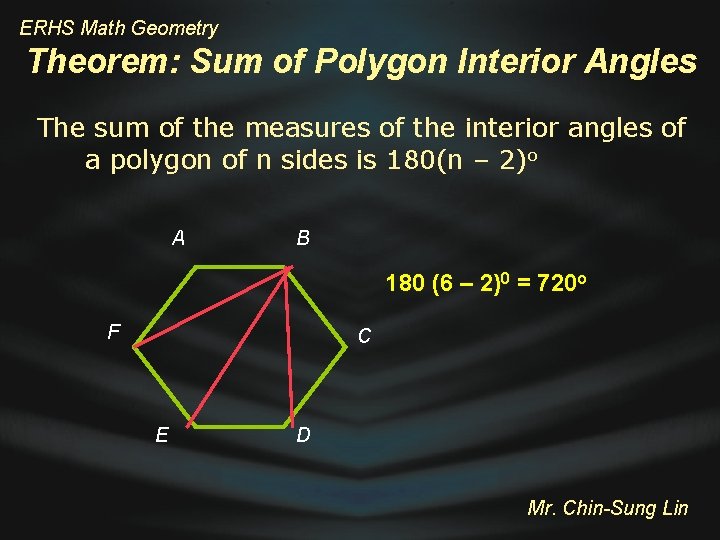
ERHS Math Geometry Theorem: Sum of Polygon Interior Angles The sum of the measures of the interior angles of a polygon of n sides is 180(n – 2)o A B 180 (6 – 2)0 = 720 o F C E D Mr. Chin-Sung Lin

ERHS Math Geometry Theorem: Sum of Polygon Exterior Angles The sum of the measures of the exterior angles of a polygon is 360 o Mr. Chin-Sung Lin

ERHS Math Geometry Theorem: Sum of Polygon Exterior Angles The sum of the measures of the exterior angles of a polygon is 360 o Sum of exterior angles = 180 n – Sum of interior angles = 180 n – 180 (n – 2) = 180 n – 180 n + 360 = 360 Mr. Chin-Sung Lin

ERHS Math Geometry Theorem: Sum of Polygon Exterior Angles The sum of the measures of the exterior angles of a polygon is 360 o A B F C Sum of exterior angles = 360 o E D Mr. Chin-Sung Lin

ERHS Math Geometry Example: Interior / Exterior Angles The measure of an exterior angle of a regular polygon is 45 o (a) Find the number of sides of the polygon (b) Find the measure of each interior angle (c) Find the sum of interior angles Mr. Chin-Sung Lin

ERHS Math Geometry Example: Interior / Exterior Angles The measure of an exterior angle of a regular polygon is 45 o (a) Find the number of sides of the polygon (b) Find the measure of each interior angle (c) Find the sum of interior angles (a) 3600/450 = 8 sides (b) 1800 – 450 = 1350 (c) 1800 (8 – 2) = 1, 0800 Mr. Chin-Sung Lin

ERHS Math Geometry Example: Interior / Exterior Angles In quadrilateral ABCD, m�A = x, m�B = 2 x – 12, m�C = x + 22, and m�D = 3 x (a) Find the measure of each interior angle (b) Find the measure of each exterior angle Mr. Chin-Sung Lin

ERHS Math Geometry Example: Interior / Exterior Angles In quadrilateral ABCD, m�A = x, m�B = 2 x – 12, m�C = x + 22, and m�D = 3 x (a) Find the measure of each interior angle (b) Find the measure of each exterior angle (a) 500, 880, 720, 1500 (b) 1300, 920, 1080, 300 Mr. Chin-Sung Lin

ERHS Math Geometry The End Mr. Chin-Sung Lin
 Eleanor roosevelt high school
Eleanor roosevelt high school Look for the two innermost diverging ridges
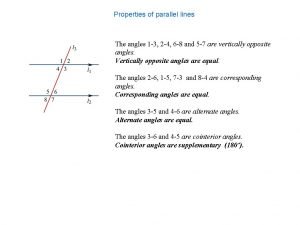
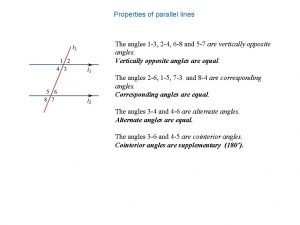
Look for the two innermost diverging ridges Parallel lines def
Parallel lines def If line a contains q(5 1)
If line a contains q(5 1) Chapter 3 parallel and perpendicular lines
Chapter 3 parallel and perpendicular lines Unit 3 parallel and perpendicular lines quiz 3-2
Unit 3 parallel and perpendicular lines quiz 3-2 Congruent angles on parallel lines
Congruent angles on parallel lines Geometry chapter 3 review parallel and perpendicular lines
Geometry chapter 3 review parallel and perpendicular lines Chapter 2 parallel lines
Chapter 2 parallel lines Books poem by eleanor farjeon question and answer
Books poem by eleanor farjeon question and answer Eleanor of aquitaine family tree
Eleanor of aquitaine family tree Eleanor rigby album revolver
Eleanor rigby album revolver Eleanor birrell
Eleanor birrell Imagine theres no lonely people
Imagine theres no lonely people Eleanor rigby biography
Eleanor rigby biography Amelia and eleanor go for a ride
Amelia and eleanor go for a ride Eleanor van tassel brush
Eleanor van tassel brush Eleanor joyce
Eleanor joyce Medieval hierarchy
Medieval hierarchy Education as human capital
Education as human capital Semantic memory
Semantic memory Eleanor
Eleanor He have dinner when his friend called
He have dinner when his friend called Eleanor margo
Eleanor margo Eleanor wynn
Eleanor wynn Eleanor marx
Eleanor marx Eleanor womack
Eleanor womack Zusammengesetze
Zusammengesetze Chapter 33 franklin d roosevelt and the shadow of war
Chapter 33 franklin d roosevelt and the shadow of war Progressivism and the republican roosevelt
Progressivism and the republican roosevelt Chapter 17 section 3 teddy roosevelt's square deal
Chapter 17 section 3 teddy roosevelt's square deal Chapter 9 section 3 teddy roosevelts square deal
Chapter 9 section 3 teddy roosevelts square deal Northern securities vs united states
Northern securities vs united states Crescenta valley high school summer school
Crescenta valley high school summer school Assignment in spanish
Assignment in spanish 5 examples of like parallel forces
5 examples of like parallel forces Parallelism refers to
Parallelism refers to Parallel sentence
Parallel sentence Parallel structure def
Parallel structure def Serial in serial out shift register truth table
Serial in serial out shift register truth table Parallelism grammar definition
Parallelism grammar definition Chapter 5 life after high school
Chapter 5 life after high school Unit 3 parallel and perpendicular lines answers
Unit 3 parallel and perpendicular lines answers Properties of parallel lines 3-2
Properties of parallel lines 3-2 Line relationships
Line relationships Square trapezoid parallelogram rectangle rhombus
Square trapezoid parallelogram rectangle rhombus Proving lines parallel
Proving lines parallel Proving lines parallel assignment
Proving lines parallel assignment Parallel lines angle property
Parallel lines angle property Angle properties of parallel lines
Angle properties of parallel lines Properties of parallel lines cut by a transversal
Properties of parallel lines cut by a transversal Proof involving parallel lines
Proof involving parallel lines Do parallel lines have the same slope
Do parallel lines have the same slope Drawing parallel lines
Drawing parallel lines Transversals and parallel lines
Transversals and parallel lines Angles formed by parallel lines cut by a transversal
Angles formed by parallel lines cut by a transversal Parallel line worksheet
Parallel line worksheet Parallel lines cut by a transversal
Parallel lines cut by a transversal Responding angles
Responding angles Proportional parts of parallel lines theorem
Proportional parts of parallel lines theorem Parallel perpendicular or neither
Parallel perpendicular or neither Parallel versus perpendicular
Parallel versus perpendicular If two nonvertical lines are parallel then
If two nonvertical lines are parallel then Lesson 12-4 slopes of parallel and perpendicular lines
Lesson 12-4 slopes of parallel and perpendicular lines Slopes of parallel and perpendicular lines assignment
Slopes of parallel and perpendicular lines assignment Non parallel transversal
Non parallel transversal Lesson 8 parallel and perpendicular lines
Lesson 8 parallel and perpendicular lines Lesson 3-7 parallel lines and transversals
Lesson 3-7 parallel lines and transversals Slopes of parallel lines are always
Slopes of parallel lines are always Parallel vs perpendicular equations
Parallel vs perpendicular equations Parallel lines
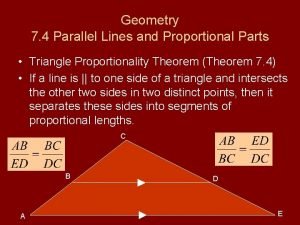
Parallel lines Geometry 7-4
Geometry 7-4 Equations of parallel lines gcse questions
Equations of parallel lines gcse questions Perpendicular line in real life
Perpendicular line in real life Electric potential unit
Electric potential unit Definition of coplanar lines
Definition of coplanar lines How to make parallel lines with a compass
How to make parallel lines with a compass Adjacent in geometry
Adjacent in geometry Parallel lines cut by a transversal solving equations
Parallel lines cut by a transversal solving equations Parallel lines relay race b answer key
Parallel lines relay race b answer key Angle relationships in parallel lines and triangles
Angle relationships in parallel lines and triangles How to tell if lines are parallel
How to tell if lines are parallel Geometry 3-5 parallel lines and triangles
Geometry 3-5 parallel lines and triangles Corresponding angles flow proof given m 5=40
Corresponding angles flow proof given m 5=40 Proving lines parallel with algebra
Proving lines parallel with algebra Parallel lines shapes
Parallel lines shapes Transversal of parallel lines find angle measures
Transversal of parallel lines find angle measures Theorems involving parallel lines
Theorems involving parallel lines Definition 23 of parallel straight lines
Definition 23 of parallel straight lines Two lines are parallel if their slopes are
Two lines are parallel if their slopes are Homework 3 proving lines parallel
Homework 3 proving lines parallel Lesson 14-2 transversals and parallel lines
Lesson 14-2 transversals and parallel lines Parallel lines shapes
Parallel lines shapes How to construct a parallel line
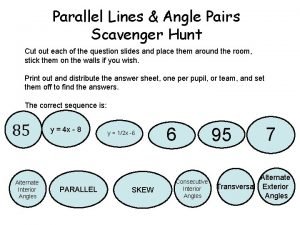
How to construct a parallel line Angle relationships scavenger hunt answer key
Angle relationships scavenger hunt answer key Parallel lines relay race
Parallel lines relay race Lesson 3-5 proving lines parallel
Lesson 3-5 proving lines parallel Proving lines are parallel worksheet answers 14-3
Proving lines are parallel worksheet answers 14-3 14-2 transversals and parallel lines
14-2 transversals and parallel lines Lesson 7.5 proportional segments between parallel lines
Lesson 7.5 proportional segments between parallel lines 3-1 parallel lines and transversals
3-1 parallel lines and transversals Parallel lines poem
Parallel lines poem Geometry skew lines
Geometry skew lines 3-3 proving lines parallel
3-3 proving lines parallel Geometry 3-5 parallel lines and triangles
Geometry 3-5 parallel lines and triangles Similar triangles relay race answers
Similar triangles relay race answers Facts about parallel lines
Facts about parallel lines Adjacent angles in parallel lines
Adjacent angles in parallel lines If line a contains q(5 1)
If line a contains q(5 1) Slopes of parallel lines are
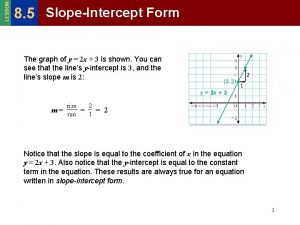
Slopes of parallel lines are E.6 equations of parallel and perpendicular lines
E.6 equations of parallel and perpendicular lines 4-4 parallel and perpendicular lines
4-4 parallel and perpendicular lines 4-2 transversals and parallel lines
4-2 transversals and parallel lines Proving lines parallel assignment
Proving lines parallel assignment Kuta software
Kuta software Writing equations of parallel lines worksheet
Writing equations of parallel lines worksheet Honors geometry parallel lines and transversals worksheet
Honors geometry parallel lines and transversals worksheet Proof parallel and perpendicular lines
Proof parallel and perpendicular lines Groups of lines
Groups of lines Directional lines in hair
Directional lines in hair Parallel lines and transversals guided notes
Parallel lines and transversals guided notes Proving lines parallel guided notes
Proving lines parallel guided notes Practice 3-3 parallel lines and the triangle-sum theorem
Practice 3-3 parallel lines and the triangle-sum theorem Pairs of lines
Pairs of lines Slopes of parallel and perpendicular lines lesson 8-1
Slopes of parallel and perpendicular lines lesson 8-1 7-2 proving lines are parallel
7-2 proving lines are parallel Lesson 4-2 transversals and parallel lines reteach answers
Lesson 4-2 transversals and parallel lines reteach answers Lesson 3-5 proving lines parallel
Lesson 3-5 proving lines parallel Lesson 3.3 proving lines parallel answers
Lesson 3.3 proving lines parallel answers Supplementary angles transversal
Supplementary angles transversal Two parallel lines lie in a plane
Two parallel lines lie in a plane Contour line definition
Contour line definition In the figure m 3 = 102 find the measure of each angle
In the figure m 3 = 102 find the measure of each angle 2-7 parallel lines and transversals
2-7 parallel lines and transversals Hair design
Hair design Angles with parallel and intersecting lines
Angles with parallel and intersecting lines Finding angle measures
Finding angle measures 5-6 parallel and perpendicular lines
5-6 parallel and perpendicular lines 6 parallel lines
6 parallel lines Proving lines parallel worksheet 3-3
Proving lines parallel worksheet 3-3 Lesson 4-3 proving lines are parallel
Lesson 4-3 proving lines are parallel 3-3 proving parallel lines
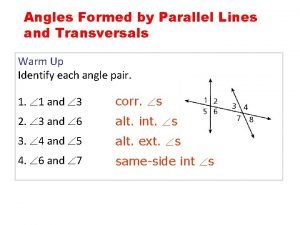
3-3 proving parallel lines Angles & lines unit warm ups
Angles & lines unit warm ups