Geometry 7 4 Parallel Lines and Proportional Parts

  • Slides: 10
Download presentation
Geometry 7. 4 Parallel Lines and Proportional Parts • Triangle Proportionality Theorem (Theorem 7.

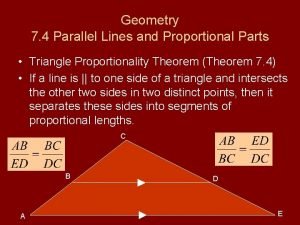
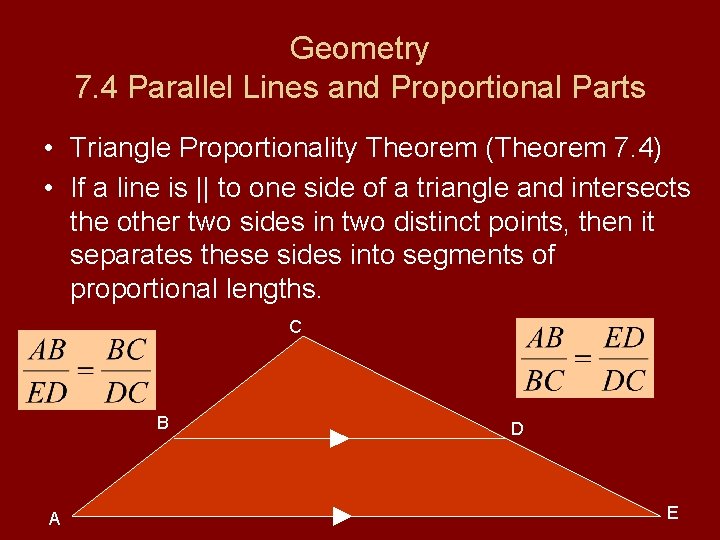
Geometry 7. 4 Parallel Lines and Proportional Parts • Triangle Proportionality Theorem (Theorem 7. 4) • If a line is || to one side of a triangle and intersects the other two sides in two distinct points, then it separates these sides into segments of proportional lengths. C B A D E

Example • In the figure, AE || BD. Find the value of x. x+5

Example • In the figure, AE || BD. Find the value of x. x+5 C x B 6 A D 8 E

Theorem 7. 5 • If a line intersects two sides of a triangle and

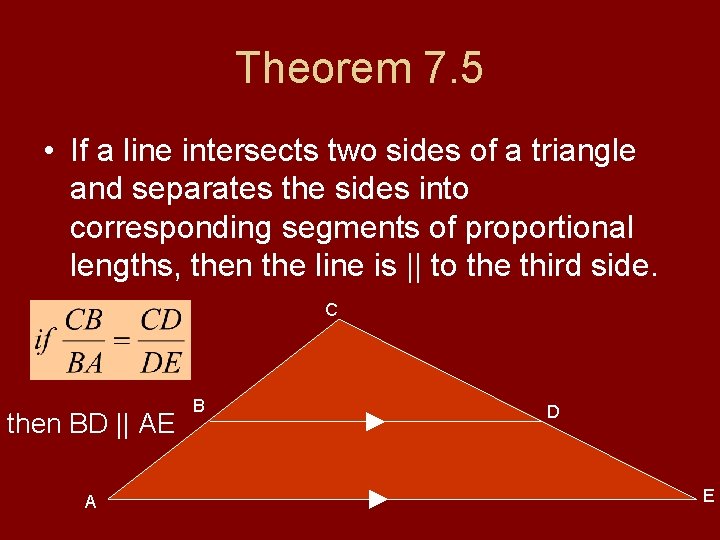
Theorem 7. 5 • If a line intersects two sides of a triangle and separates the sides into corresponding segments of proportional lengths, then the line is || to the third side. C then BD || AE A B D E

Example • Determine whether DE || BC. • Yes because 6/3 = 8/4 A

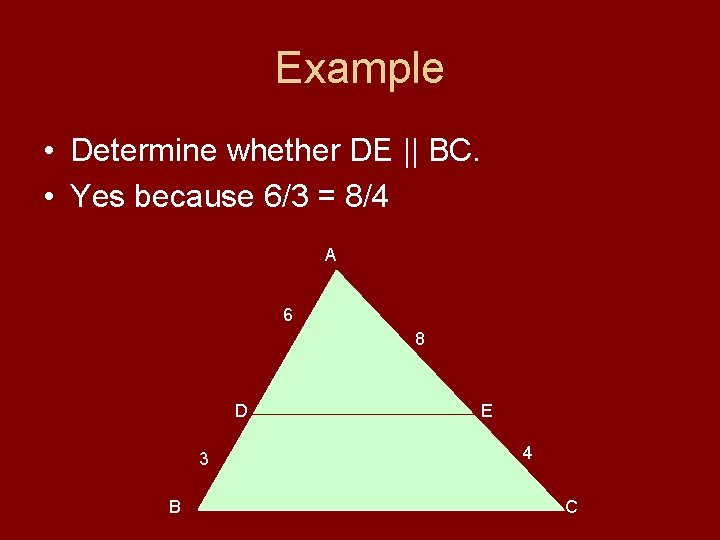
Example • Determine whether DE || BC. • Yes because 6/3 = 8/4 A 6 8 D 3 B E 4 C

Theorem 7. 6: Triangle Midsegment Theorem • Midsegment: Midsegment A segment with endpoints that

Theorem 7. 6: Triangle Midsegment Theorem • Midsegment: Midsegment A segment with endpoints that are midpoints of two sides of the triangle. • A midsegment of a triangle is || to one side of the triangle and its length is one-half the length of the third side. A D B E C

Example • Refer to the figure and Example #3 on page 407 • The

Example • Refer to the figure and Example #3 on page 407 • The example uses the midpoint formula, the slope formula and the distance formula to verify coordinates of midpoint, parallelism, and lengths of segments.

Corollary 7. 1 • If 3 or more || lines intersect 2 transversals, then

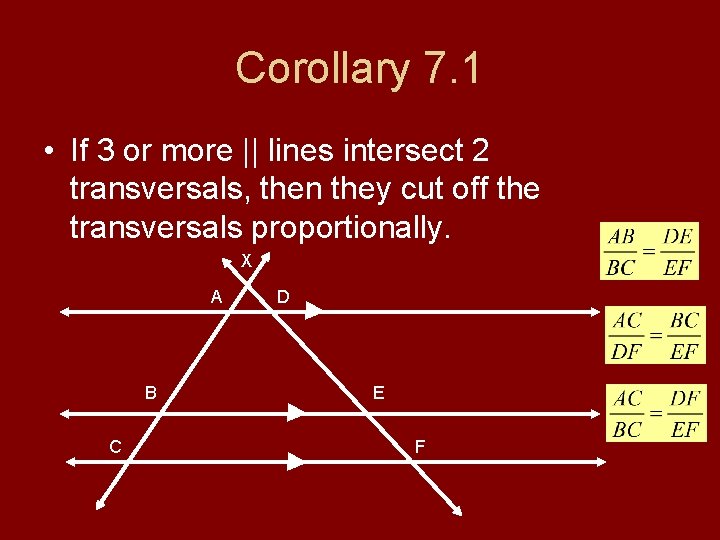
Corollary 7. 1 • If 3 or more || lines intersect 2 transversals, then they cut off the transversals proportionally. X A B C D E F

Example • In the figure, a || b || c. Find the value of

Example • In the figure, a || b || c. Find the value of x. • 20 15 9 12 x a b c

Corollary 7. 2 • If 3 or more || lines cut off segments on

Corollary 7. 2 • If 3 or more || lines cut off segments on one transversal, then they cut off segments on every transversal.

Homework #48 • p. 411 13 -18, 21 -29 odd, 32 -38 even, 54

Homework #48 • p. 411 13 -18, 21 -29 odd, 32 -38 even, 54 -55

GEOMETRY Angles and Parallel Lines Intersecting Lines LinesGEOMETRY Angles and Parallel Lines Intersecting Lines Lines
Lines and Angles Geometry PARALLEL LINES Two linesLines and Angles Geometry PARALLEL LINES Two lines
Parallel and Perpendicular Lines Parallel Lines Two linesParallel and Perpendicular Lines Parallel Lines Two lines
Parallel Lines Transversals Geometry Parallel Lines and TransversalsParallel Lines Transversals Geometry Parallel Lines and Transversals
Pairs of Lines 1 Parallel Lines Parallel linesPairs of Lines 1 Parallel Lines Parallel lines
Parallel Lines Introduction What are parallel lines LinesParallel Lines Introduction What are parallel lines Lines
PARALLEL LINES TRANSVERSALS PARALLEL LINES ARE LINES THATPARALLEL LINES TRANSVERSALS PARALLEL LINES ARE LINES THAT
Parallel and Perpendicular Assignment Parallel Lines Parallel linesParallel and Perpendicular Assignment Parallel Lines Parallel lines
Parallel Lines Transversals Mrs Wedgwood Geometry Parallel LinesParallel Lines Transversals Mrs Wedgwood Geometry Parallel Lines