Unit 2 Parallel lines and Transversals day 11

Unit 2: Parallel lines and Transversals (day 11) Objective: SWBAT identify special angle pairs and their properties. (3. 1/3. 2) **hw/hw log/storybook: “Parallel Lines/Transversals”/colored pencils Put Cube in your Block Box in front (make sure you tabbed cube 1 with name, block) Bucket A: SOL/TEI questions (stapled, make sure in order and name is on it) Regular Geometry: workbook p. 59 & p. 63/Quiz corrections on desk (day 5, 8, 9) Honors Geometry: worksheet/Quiz corrections on desk (day 5, 8, 9) ** Warm-Up: Correct Test on separate piece of paper (use notes, prior quizzes, etc) Homework (day 11)- check odd answers in text: p. 144 (11 -27 odd, 31 -35 odd) p. 152 (1 -9 odd, 13 -19 odd, 23) Pearsonsuccess Due Friday

Unit 2 (Divider 2) Parallel Lines and Transversals • Lessons 11 -16

Compasses • Please return the compass you borrowed during the test ASAP

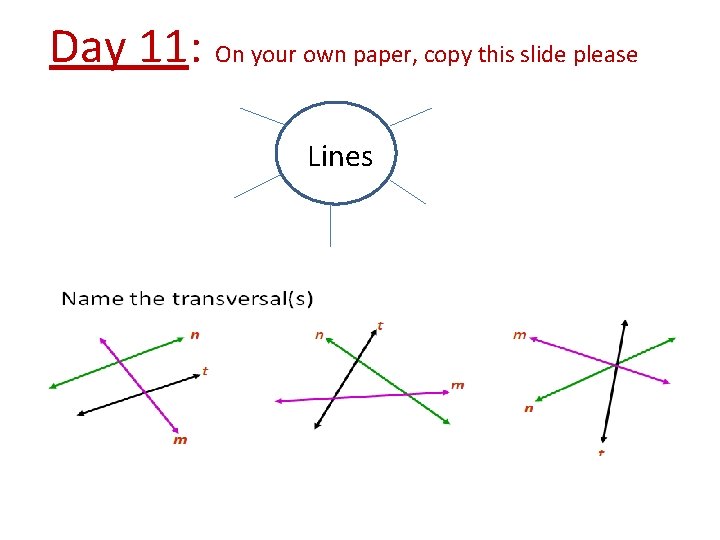
Day 11: On your own paper, copy this slide please Lines

What angle pairs have NO transversal; draw an example. Special Angles formed by a transversal:

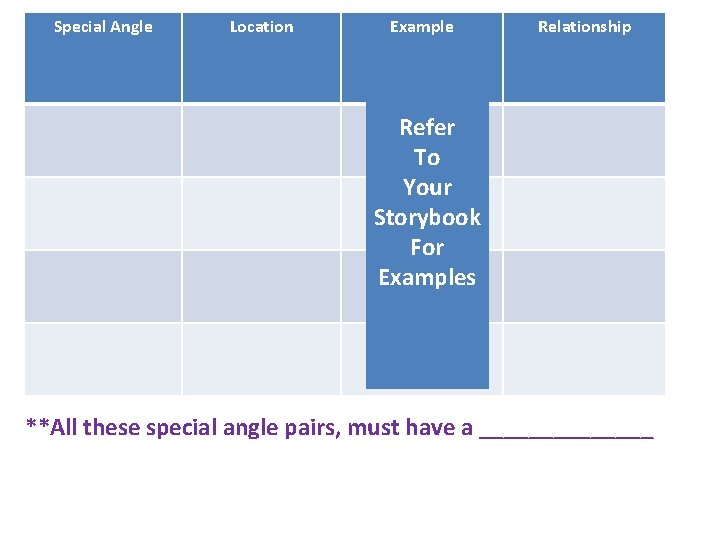
Special Angle Location Example Relationship Refer To Your Storybook For Examples **All these special angle pairs, must have a _______

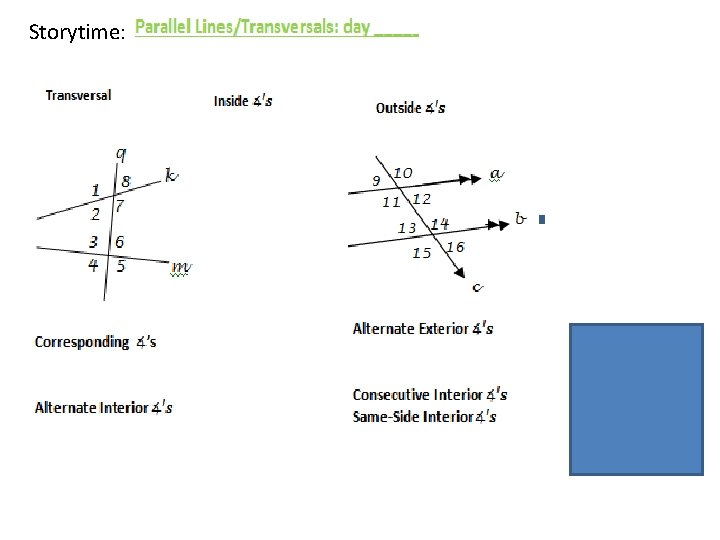
Storytime: “Parallel Lines/Transversals” X O O X O X X + O = 180

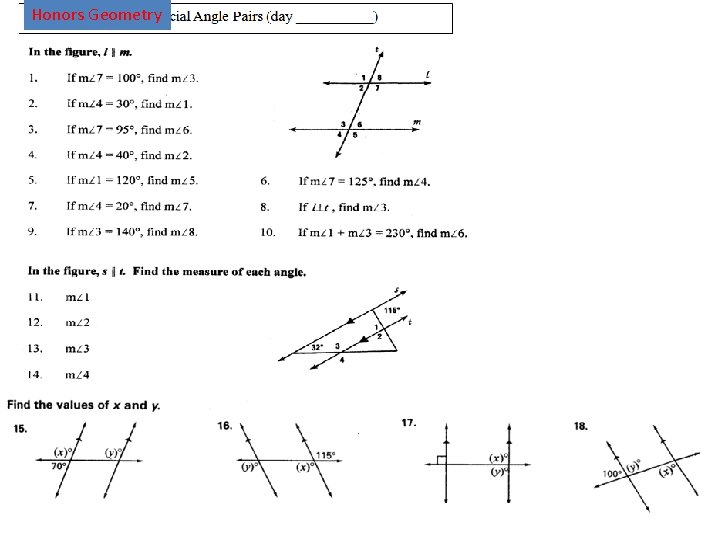
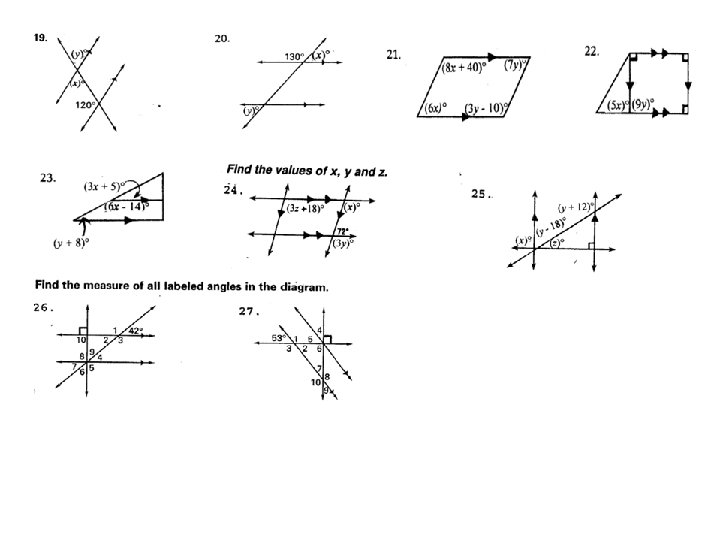
Honors Geometry

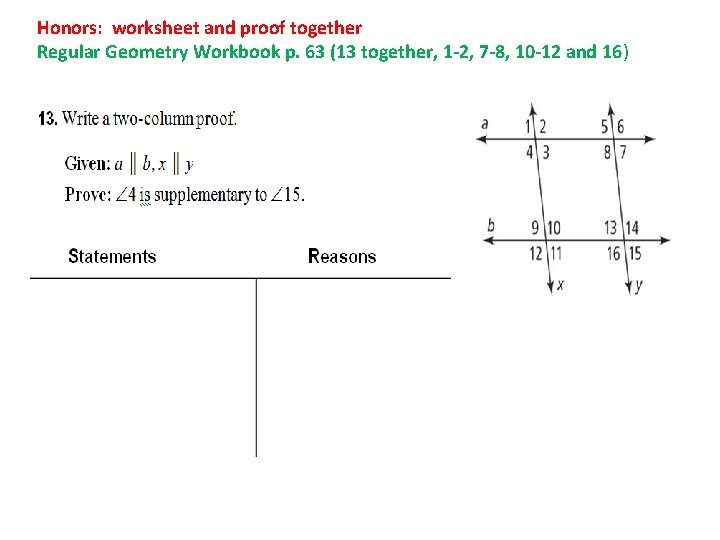
Honors: worksheet and proof together Regular Geometry Workbook p. 63 (13 together, 1 -2, 7 -8, 10 -12 and 16)

Regular Geometry Workbook p. 59 (5, 8, 12, 27)

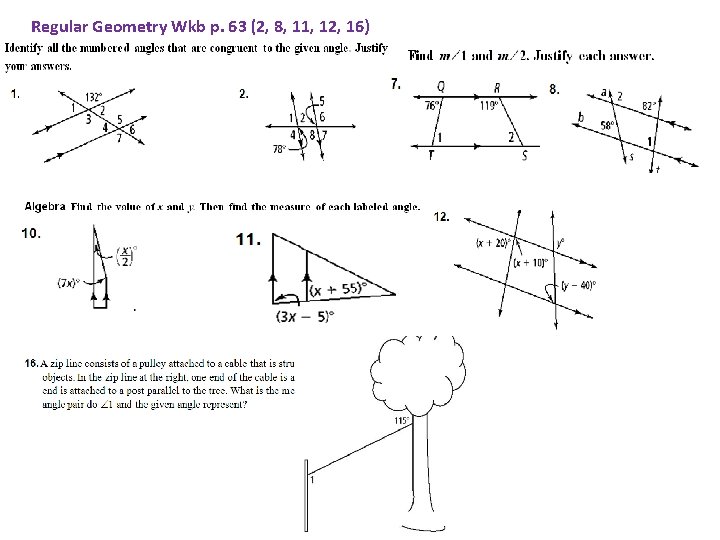
Regular Geometry Wkb p. 63 (2, 8, 11, 12, 16)

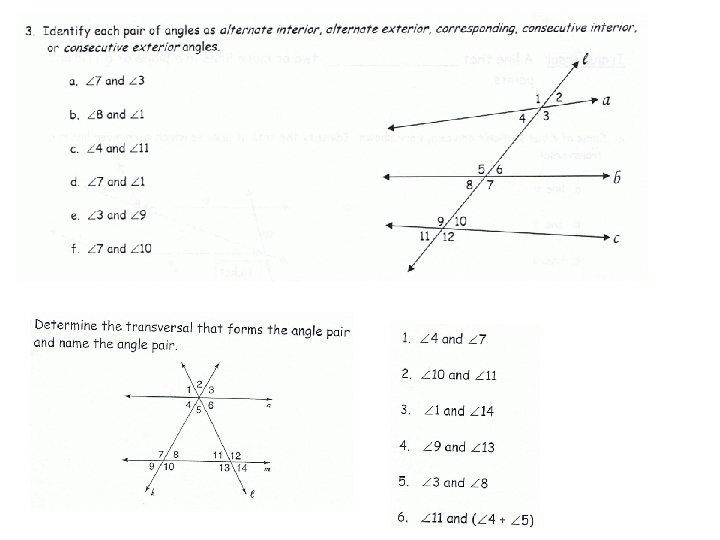
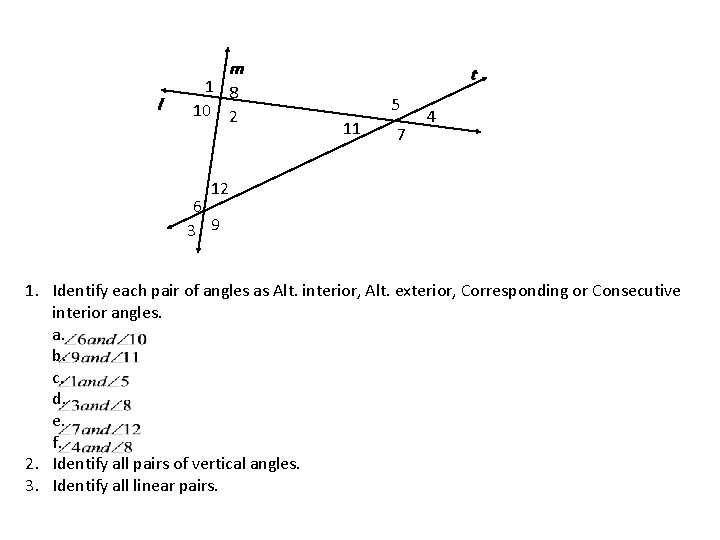
m l 1 8 10 2 t 5 11 7 4 12 6 3 9 1. Identify each pair of angles as Alt. interior, Alt. exterior, Corresponding or Consecutive interior angles. a. b. c. d. e. f. 2. Identify all pairs of vertical angles. 3. Identify all linear pairs.

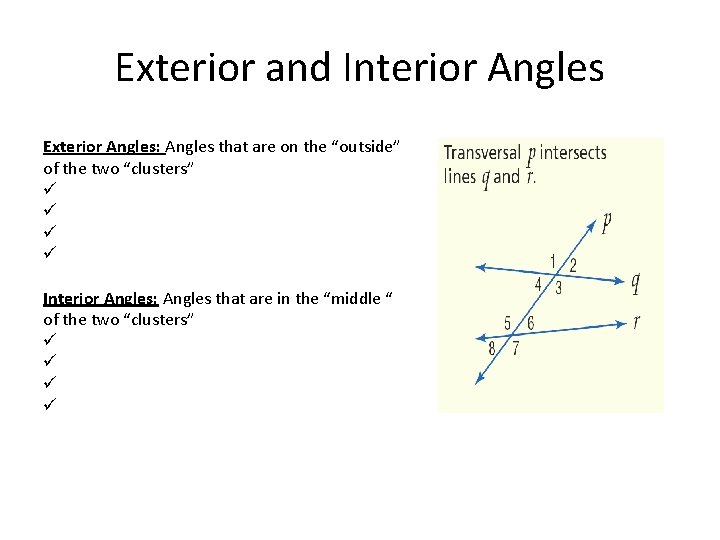
Exterior and Interior Angles Exterior Angles: Angles that are on the “outside” of the two “clusters” ü ü Interior Angles: Angles that are in the “middle “ of the two “clusters” ü ü

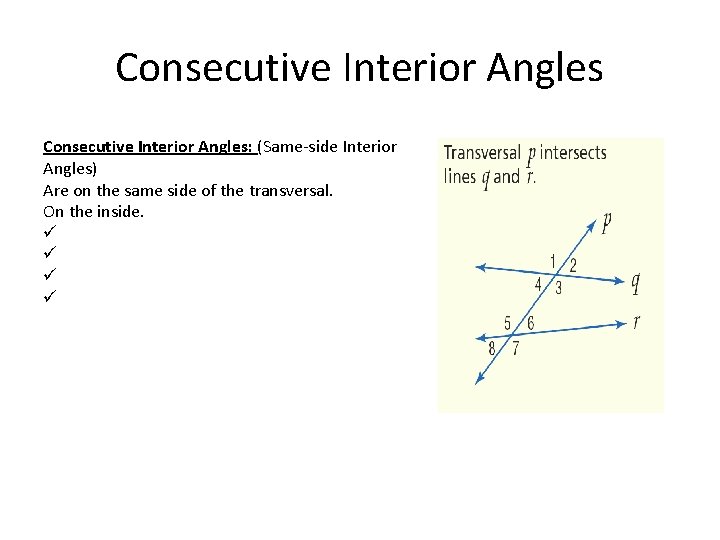
Consecutive Interior Angles: (Same-side Interior Angles) Are on the same side of the transversal. On the inside. ü ü

Alternate Exterior and Alternate Interior Angles Alternate Exterior Angles: Are on the opposite sides (or they alternate sides) of the transversal. Are on the outside. ü ü Alternate Interior Angles: Are on the opposite sides of the transversal. Are on the inside. ü ü

Corresponding Angles: Occupy the same place in the different clusters. ü ü

Parallel Lines • Parallel lines are coplanar lines that do not intersect. • Arrows are used to indicate lines are parallel. • The symbol used for parallel lines is ||. In the above figure, the arrows show that line AB is parallel to line CD. With symbols we denote, . Lesson 2 -3: Pairs of Lines 22

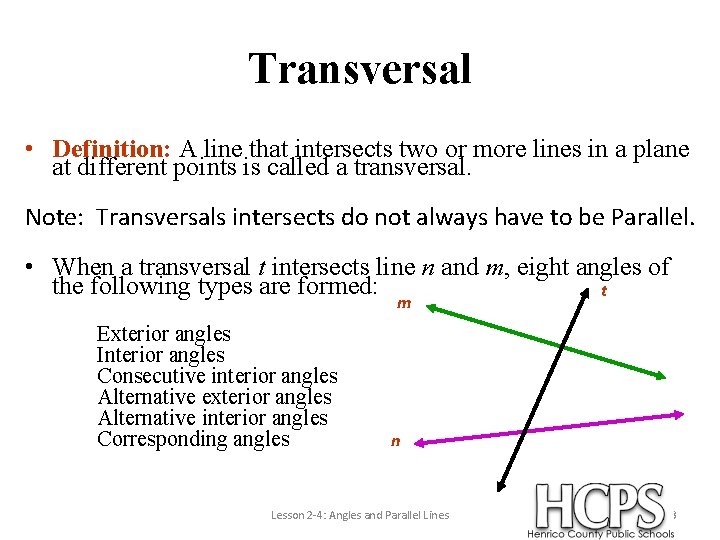
Transversal • Definition: A line that intersects two or more lines in a plane at different points is called a transversal. Note: Transversals intersects do not always have to be Parallel. • When a transversal t intersects line n and m, eight angles of the following types are formed: t m Exterior angles Interior angles Consecutive interior angles Alternative exterior angles Alternative interior angles Corresponding angles n Lesson 2 -4: Angles and Parallel Lines 23

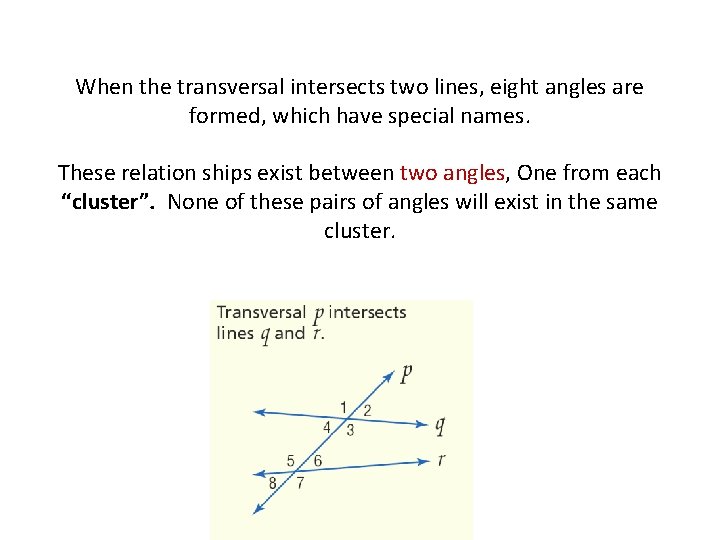
When the transversal intersects two lines, eight angles are formed, which have special names. These relation ships exist between two angles, One from each “cluster”. None of these pairs of angles will exist in the same cluster.

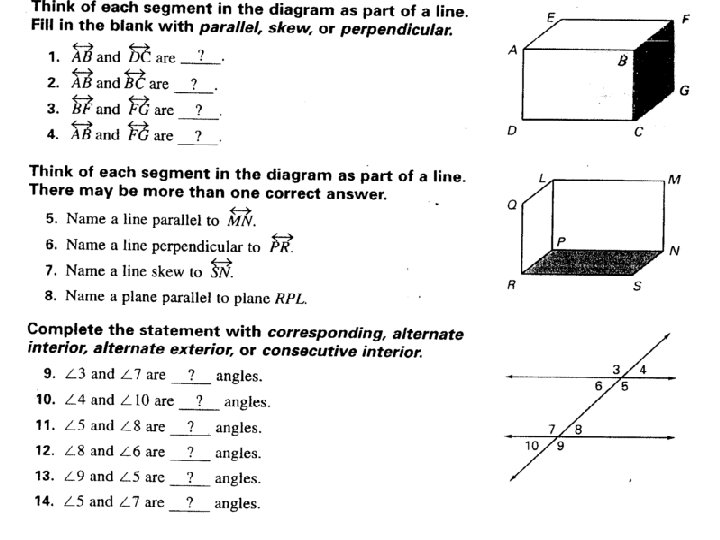
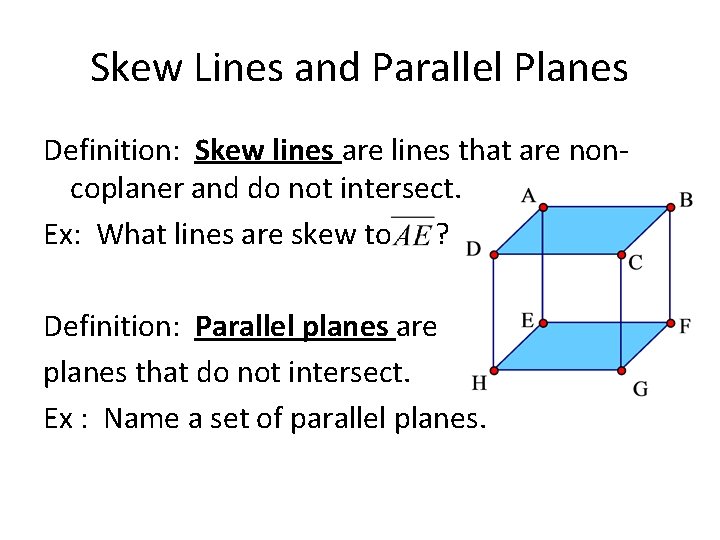
Skew Lines and Parallel Planes Definition: Skew lines are lines that are noncoplaner and do not intersect. Ex: What lines are skew to ? Definition: Parallel planes are planes that do not intersect. Ex : Name a set of parallel planes.

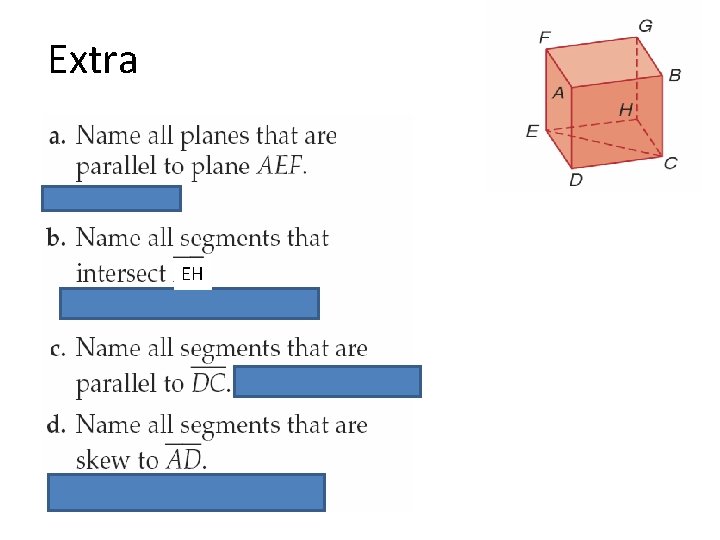
Extra EH