Geometry Lesson 7 4 Parallel Lines and Proportional

  • Slides: 17
Download presentation
Geometry Lesson 7 – 4 Parallel Lines and Proportional Parts Objective: Use proportional parts

Geometry Lesson 7 – 4 Parallel Lines and Proportional Parts Objective: Use proportional parts within triangles. Use proportional parts with parallel lines.

Theorem Triangle Proportionality Theorem l If a line is parallel to one side of

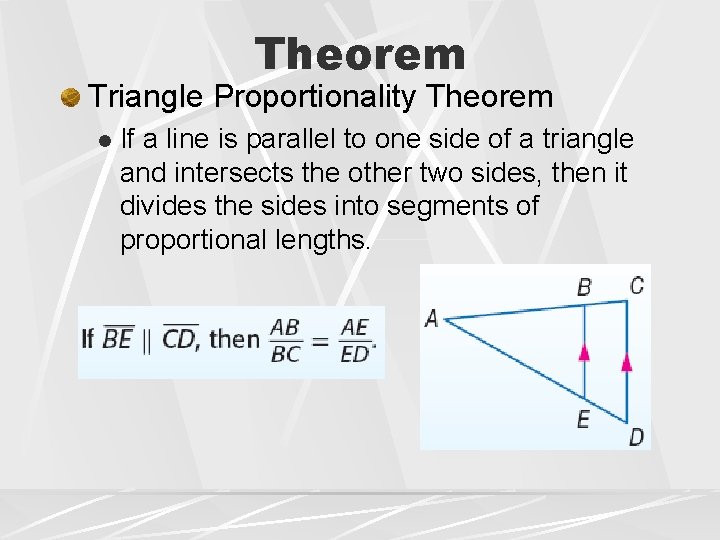
Theorem Triangle Proportionality Theorem l If a line is parallel to one side of a triangle and intersects the other two sides, then it divides the sides into segments of proportional lengths.

In triangle PQR ST II RQ. If PT = 7. 5, TQ = 3,

In triangle PQR ST II RQ. If PT = 7. 5, TQ = 3, and SR = 2. 5, find PS and PR. x Method from last section: 7. 5 3 3 x = 18. 75 x = 6. 25 PS = 6. 25 PR = 8. 75 2. 5 10. 5 x = 7. 5 x + 18. 75 3 x = 18. 75 x = 6. 25

If PS = 12. 5, SR = 5, and PT = 15, find TQ.

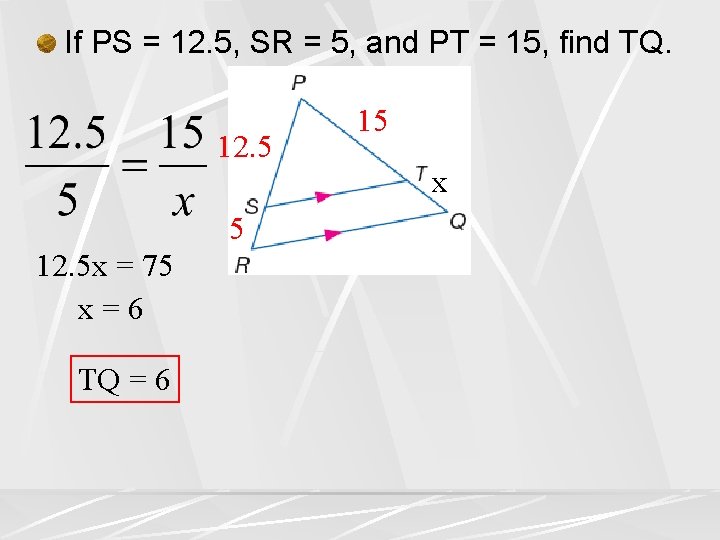
If PS = 12. 5, SR = 5, and PT = 15, find TQ. 12. 5 5 12. 5 x = 75 x=6 TQ = 6 15 x

Theorem Converse of Triangle Proportionality Theorem l If a line intersects two sides of

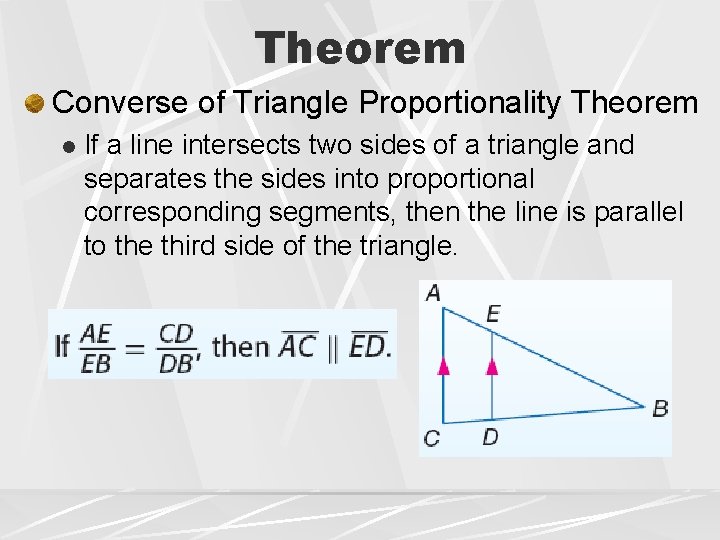
Theorem Converse of Triangle Proportionality Theorem l If a line intersects two sides of a triangle and separates the sides into proportional corresponding segments, then the line is parallel to the third side of the triangle.

In triangle DEF, EH = 3, HF = 9, and DG is one-third the

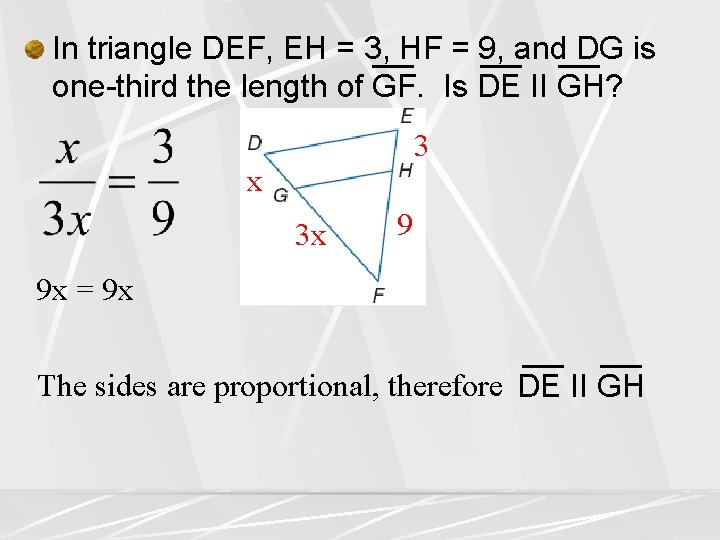
In triangle DEF, EH = 3, HF = 9, and DG is one-third the length of GF. Is DE II GH? 3 x 3 x 9 9 x = 9 x The sides are proportional, therefore DE II GH

DG is half the length of GF, EH = 6, and HF = 10.

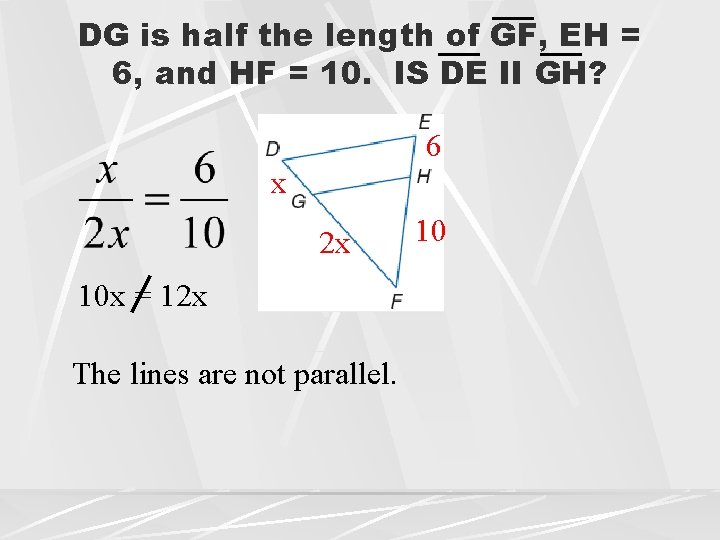
DG is half the length of GF, EH = 6, and HF = 10. IS DE II GH? 6 x 2 x 10 x = 12 x The lines are not parallel. 10

Midsegment of a triangle l A segment with endpoints that are the midpoints of

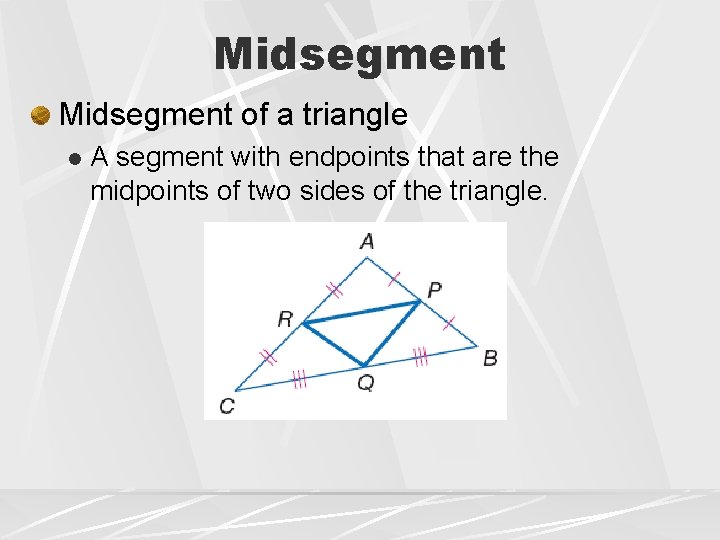
Midsegment of a triangle l A segment with endpoints that are the midpoints of two sides of the triangle.

Theorem Triangle Midsegment Theorem l A midsegment of a triangle is parallel to one

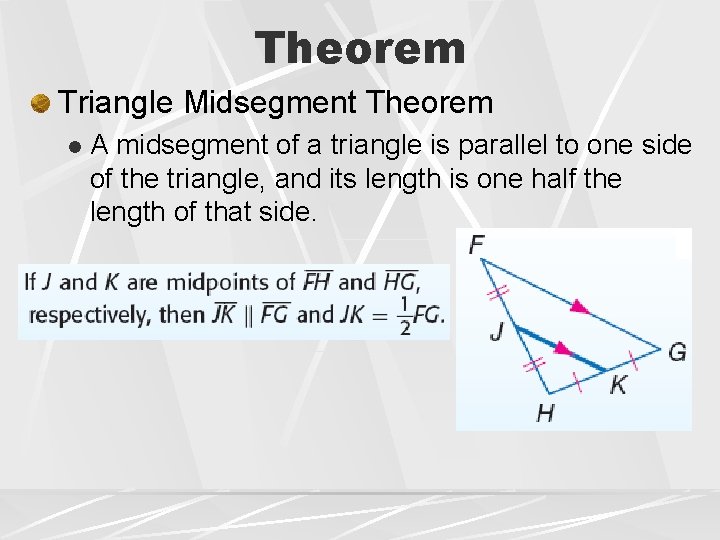
Theorem Triangle Midsegment Theorem l A midsegment of a triangle is parallel to one side of the triangle, and its length is one half the length of that side.

XY and XZ are midsegments of the triangle. Find XZ 6. 5 ST 7

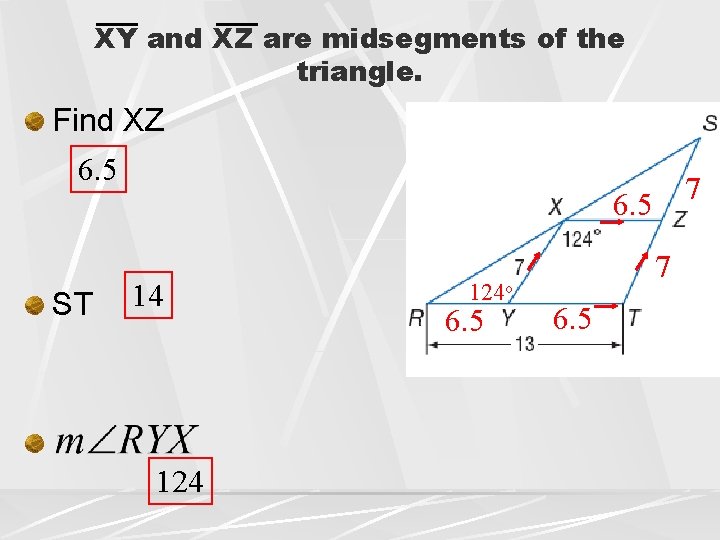
XY and XZ are midsegments of the triangle. Find XZ 6. 5 ST 7 6. 5 14 124 o 6. 5 7 6. 5

Find each measure DE 7. 5 DB 9. 2 82 9. 2 7. 5

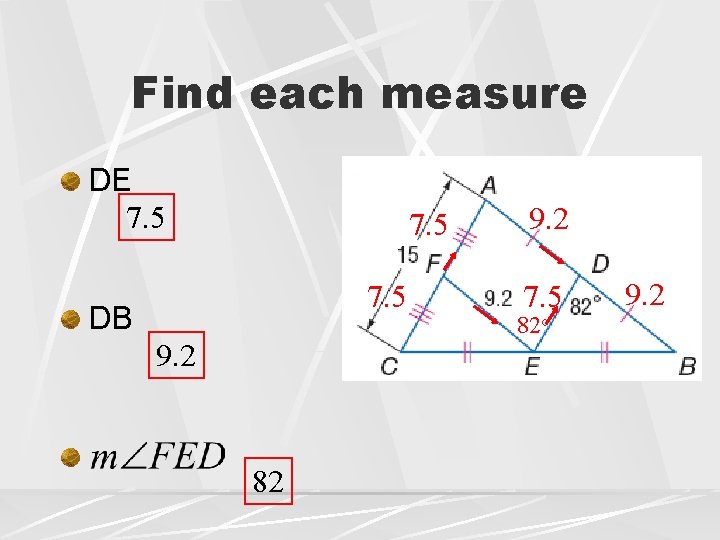
Find each measure DE 7. 5 DB 9. 2 82 9. 2 7. 5 82 o 9. 2

Proportional Parts of Parallel Lines If three or more parallel lines intersect two transversals,

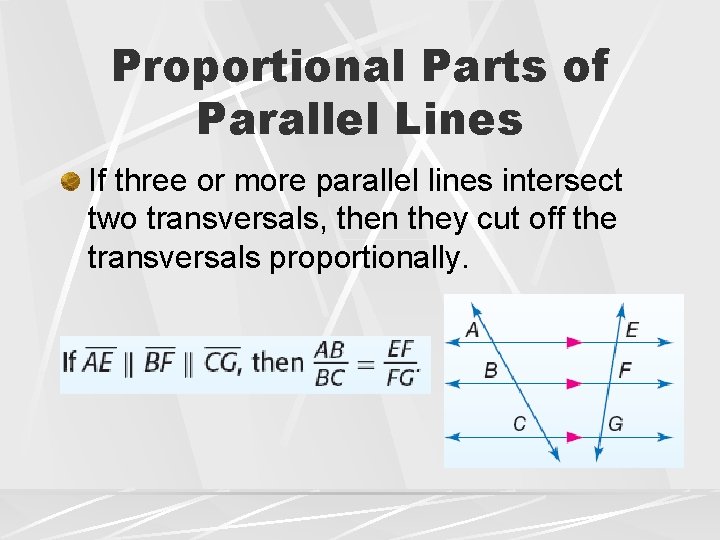
Proportional Parts of Parallel Lines If three or more parallel lines intersect two transversals, then they cut off the transversals proportionally.

Frontage is the measurement of a property’s boundary that runs along the side of

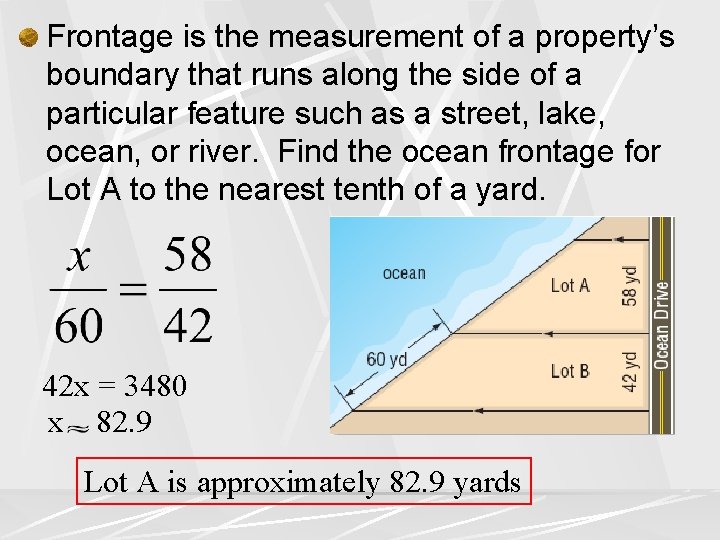
Frontage is the measurement of a property’s boundary that runs along the side of a particular feature such as a street, lake, ocean, or river. Find the ocean frontage for Lot A to the nearest tenth of a yard. 42 x = 3480 x 82. 9 Lot A is approximately 82. 9 yards

Corollary Congruent Parts of Parallel Lines l If three or more parallel lines cut

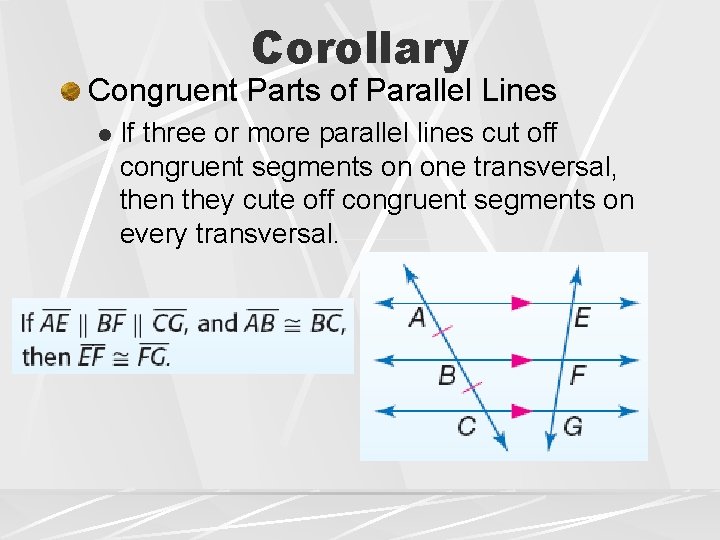
Corollary Congruent Parts of Parallel Lines l If three or more parallel lines cut off congruent segments on one transversal, then they cute off congruent segments on every transversal.

Find x and y 3 y + 8 = 5 y - 7 15

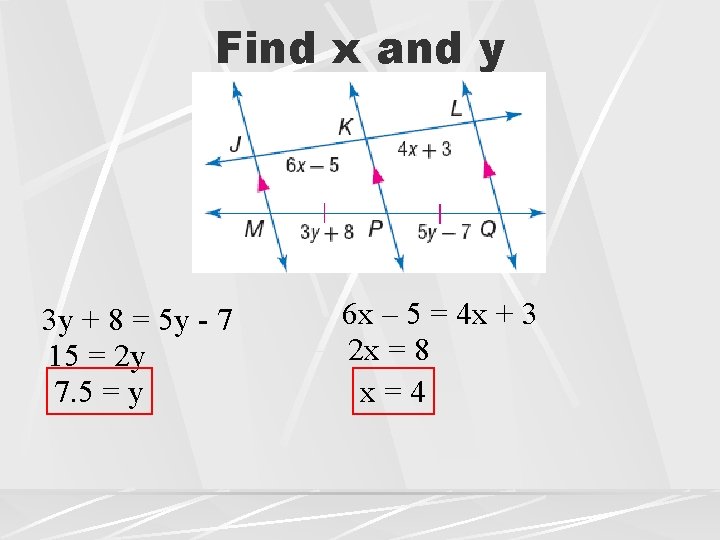
Find x and y 3 y + 8 = 5 y - 7 15 = 2 y 7. 5 = y 6 x – 5 = 4 x + 3 2 x = 8 x=4

Find x 2 x + 1 = 3 x - 5 6=x 3 x

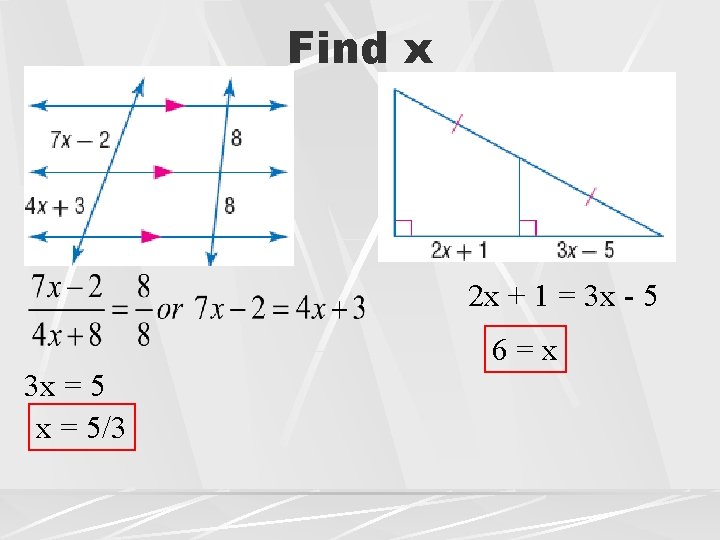
Find x 2 x + 1 = 3 x - 5 6=x 3 x = 5/3

Homework Pg. 489 1 – 9 all, 10 – 26 E, 54 – 66

Homework Pg. 489 1 – 9 all, 10 – 26 E, 54 – 66 E

GEOMETRY Angles and Parallel Lines Intersecting Lines LinesGEOMETRY Angles and Parallel Lines Intersecting Lines Lines
Lines and Angles Geometry PARALLEL LINES Two linesLines and Angles Geometry PARALLEL LINES Two lines
Parallel and Perpendicular Lines Parallel Lines Two linesParallel and Perpendicular Lines Parallel Lines Two lines
Parallel Lines Transversals Geometry Parallel Lines and TransversalsParallel Lines Transversals Geometry Parallel Lines and Transversals
Pairs of Lines 1 Parallel Lines Parallel linesPairs of Lines 1 Parallel Lines Parallel lines
Parallel Lines Introduction What are parallel lines LinesParallel Lines Introduction What are parallel lines Lines
PARALLEL LINES TRANSVERSALS PARALLEL LINES ARE LINES THATPARALLEL LINES TRANSVERSALS PARALLEL LINES ARE LINES THAT
Parallel and Perpendicular Assignment Parallel Lines Parallel linesParallel and Perpendicular Assignment Parallel Lines Parallel lines
Parallel Lines Transversals Mrs Wedgwood Geometry Parallel LinesParallel Lines Transversals Mrs Wedgwood Geometry Parallel Lines
Geometry 7 4 Parallel Lines and Proportional PartsGeometry 7 4 Parallel Lines and Proportional Parts
Geometry 7 6 Proportional Lengths Proportional Lengths nGeometry 7 6 Proportional Lengths Proportional Lengths n
Lesson 6 4 Parallel Lines and Proportional PartsLesson 6 4 Parallel Lines and Proportional Parts
Parallel Lines and Proportional Parts Lesson 5 4Parallel Lines and Proportional Parts Lesson 5 4
Angles and Parallel Lines Intersecting Lines Lines thatAngles and Parallel Lines Intersecting Lines Lines that
Parallel Lines and Transversals Angles and parallel linesParallel Lines and Transversals Angles and parallel lines
Parallel Lines and Transversals Angles and Parallel LinesParallel Lines and Transversals Angles and Parallel Lines