Bell work 3 5 Parallel Lines and Triangles

Bell work:

3. 5: Parallel Lines and Triangles

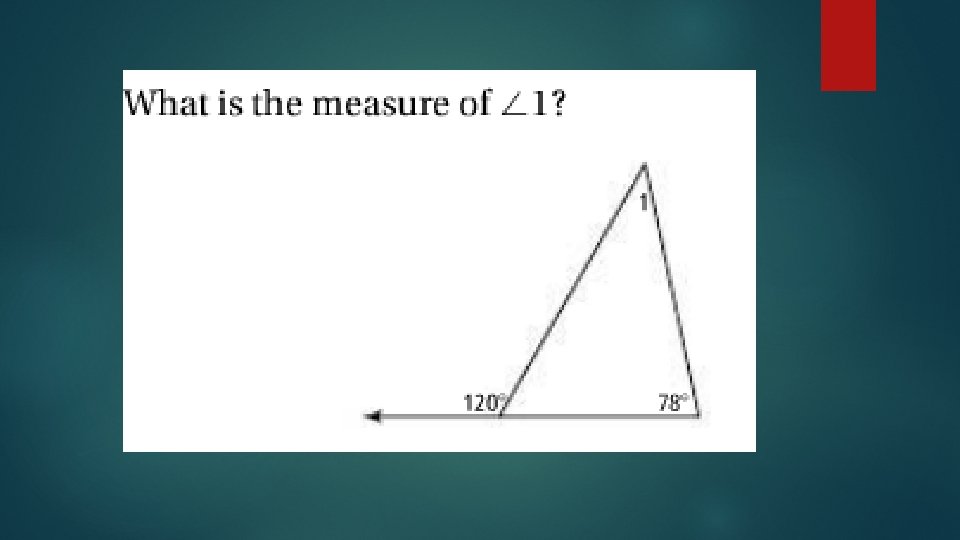
In the previous proof, we used an auxiliary line. An auxiliary line is a new line that you draw to help you prove something. An exterior angle of a polygon is an angle formed by a side and the extension of an adjacent side. The two non-adjacent interior angles are its remote interior angles Theorem 3 -12: Triangle Exterior Angle Theorem The measure of each exterior angle of a triangle is equal to the sum of the measures of its remote interior angles

Using the Triangle theorems A triangle has two interior angles measuring 35 and 95 degrees, respectively. 1. What is the other interior angle? 2. What is the exterior angle to those two remote interior angles? 3. Find one other exterior angle 4. How many exterior angles does a triangle have?

Chapter 3 Review What is a transversal? When lines are parallel, what can we conclude about the angles? When special angles are congruent, what can we conclude about the lines? What theorems can we use when we have multiple parallel or perpendicular lines? What are the two equations we use for lines? How can I tell if two equations are parallel or perpendicular?

Chapter 3 Review

Homework: Finish the Chapter 3 Test on pages 211 -212. Honors: As above, and complete a proof of theorem 3 -12 Reminder: Proof practice website problems must be submitted by Saturday!

Chapter 3 Test