Proofs Involving Parallel Lines Part 1 Given Parallel

Proofs Involving Parallel Lines Part 1: Given Parallel Lines When you know that you are working with parallel lines you can use theorems we learned yesterdays as reasons within your proof: A. Alternate interior angles are congruent, when lines are parallel. B. Corresponding angles are congruent, when lines are parallel. C. Alternate exterior angles are congruent, when lines are parallel. D. Same side interior angles are supplementary, when lines are parallel

Examples: Statements 1) , and Reasons 1) Given 2) <1 = <A, <2 = <B 2) Alternate Interior angles when lines //. 3) <A = <B 3) Substitution Postulate ,

Part 2: Proving Lines Parallel To prove two lines parallel we can use the converse of many of our theorems involving parallel lines. A. If a pair of alternate interior angles are congruent, then the lines are parallel. If a pair of corresponding angles are congruent, then the lines are parallel. If a pair of same side interior angles are supplementary, then the lines are parallel. B. C. There are two more methods of proving lines are parallel. D. Two lines parallel to the same line are parallel to each other. (Transitive Property) l m p If and then

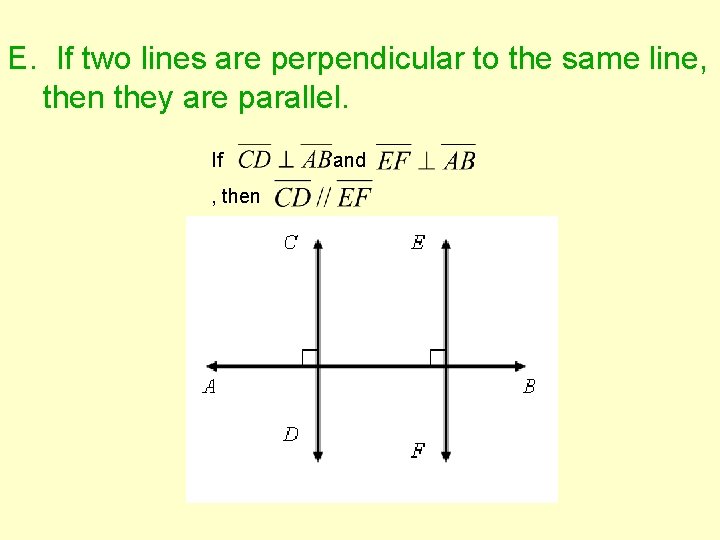
E. If two lines are perpendicular to the same line, then they are parallel. If , then and

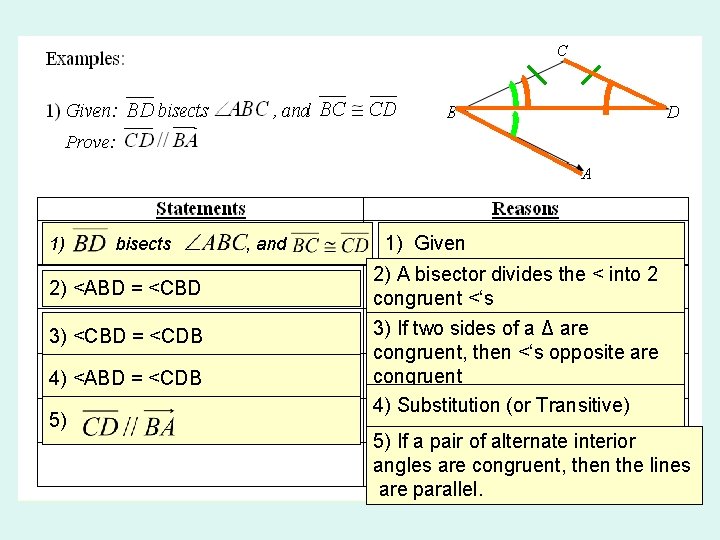
1) bisects 2) <ABD = <CBD 3) <CBD = <CDB 4) <ABD = <CDB 5) , and 1) Given 2) A bisector divides the < into 2 congruent <‘s 3) If two sides of a Δ are congruent, then <‘s opposite are congruent 4) Substitution (or Transitive) 5) If a pair of alternate interior angles are congruent, then the lines are parallel.

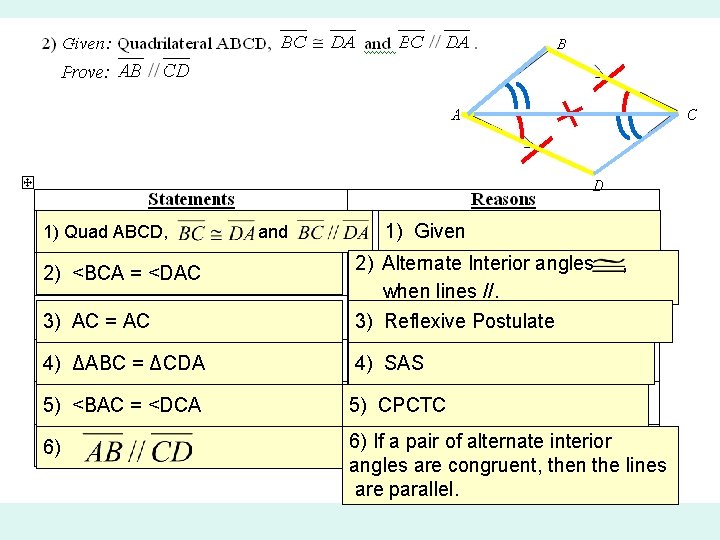
1) Quad ABCD, and 1) Given 3) AC = AC 2) Alternate Interior angles when lines //. 3) Reflexive Postulate 4) ΔABC = ΔCDA 4) SAS 5) <BAC = <DCA 5) CPCTC 6) 6) If a pair of alternate interior angles are congruent, then the lines are parallel. 2) <BCA = <DAC ,