3 3 Proving Lines Parallel Objectives Students will

3 -3 Proving Lines Parallel

Objectives � Students will be able to ◦ Determine whether two lines are parallel ◦ Write flow proofs ◦ Define and apply the converse of theorems from the previous section

Essential Understanding � You can use certain angle pairs to determine if two lines are parallel

� What is the corresponding angles theorem? � If a transversal intersects two parallel lines, then corresponding angles are congruent � What is the converse of the corresponding angles theorem? � If two lines and a transversal form congruent corresponding angles, then the lines are parallel

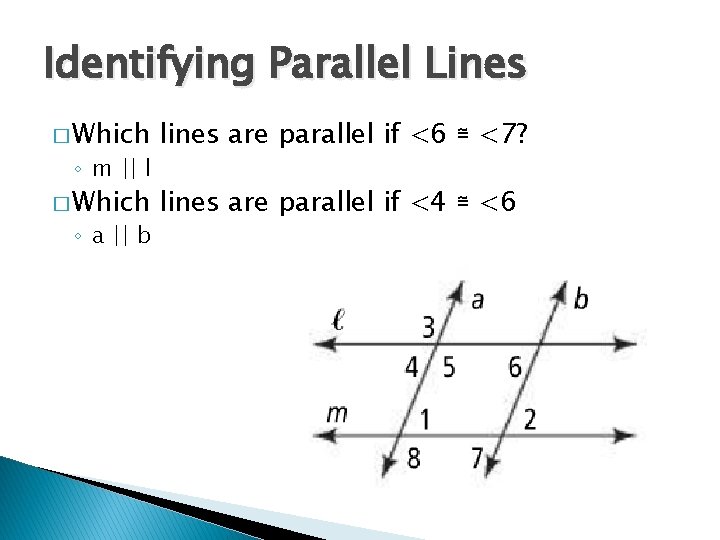
Identifying Parallel Lines � Which lines are parallel if <6 ≅ <7? � Which lines are parallel if <4 ≅ <6 ◦ m || l ◦ a || b

Converse of the Alternate Interior Angles Theorem � If two lines and a transversal form alternate interior angles that are congruent, then the two lines are parallel

Converse of the Same-Side Interior Angles Theorem � If two lines and a transversal form same side interior angles that are supplementary, then the two lines are parallel.

Converse of the Alternate Exterior Angles Theorem � If two lines and a transversal form alternate exterior angles that are congruent, then the two lines are parallel.

Summary � If corresponding angles are congruent, then the lines are parallel � If alternate interior lines are congruent, then the lines are parallel � If alternate exterior lines are congruent, then the lines are parallel � If same side interior angles are supplementary, then the lines are parallel

Things to Keep in Mind… � In order to use theorems relating to parallel lines, you must first prove the lines are parallel if it is not given/stated in the problem. � Even if lines appear to be parallel, you cannot assume they are parallel � Always assume diagrams are NOT drawn to scale, unless otherwise stated

Flow Proof � Third way to write a proof � In a flow proof, arrows show the flow, or the logical connections, between statements. � Reasons are written below the statements

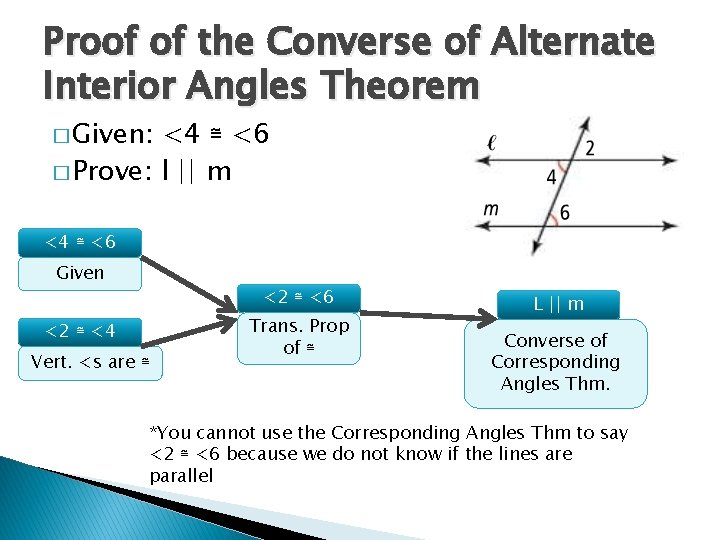
Proof of the Converse of Alternate Interior Angles Theorem � Given: <4 ≅ <6 � Prove: l || m <4 ≅ <6 Given <2 ≅ <6 <2 ≅ <4 Vert. <s are ≅ Trans. Prop of ≅ L || m Converse of Corresponding Angles Thm. *You cannot use the Corresponding Angles Thm to say <2 ≅ <6 because we do not know if the lines are parallel

Write a flow proof � Given: � Prove: m<5 = 40, m<2 = 140 a || b � Start with what you know ◦ The given statement ◦ What you can conclude from your picture. � What you need to know ◦ Which theorem you can use to show a||b

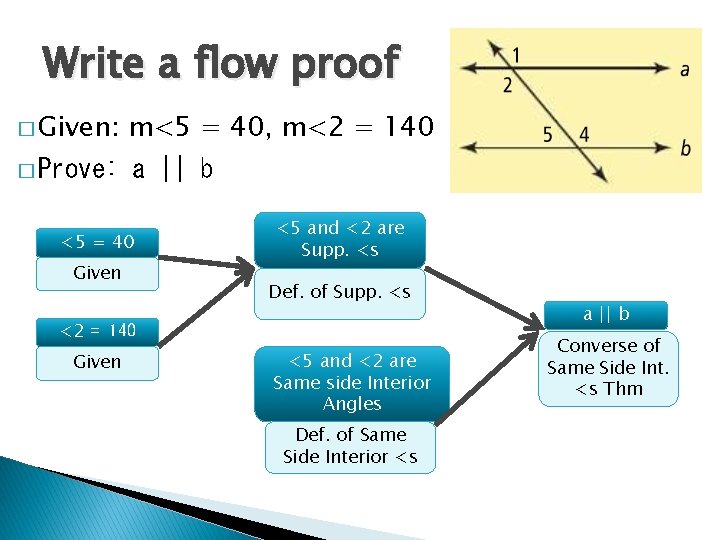
Write a flow proof � Given: m<5 = 40, m<2 = 140 � Prove: a || b <5 = 40 Given <5 and <2 are Supp. <s Def. of Supp. <s <2 = 140 Given <5 and <2 are Same side Interior Angles Def. of Same Side Interior <s a || b Converse of Same Side Int. <s Thm

� You now have four ways to prove if two lines are parallel

Using Algebra � What is the value of x for which a || b? � Work backwards. What must be true of the given angles for a and b to be parallel? � How are the angles related? ◦ Same side interior ◦ Therefore, they must add to be 180

Using Algebra � What is the value of x for which a || b? � Work backwards. What must be true of the given angles for a and b to be parallel? � How are the angles related? ◦ Corresponding Angles ◦ Therefore, the angles are congruent

Homework � Pg. 160 – 162 � # 7 – 16, 21 – 24, 28, 32 � 16 Problems