Parallel and Perpendicular Lines SlopeIntercept Form From Intermediate


- Slides: 5

Parallel and Perpendicular Lines

Slope-Intercept Form From Intermediate Algebra • Useful for graphing since m is the slope and b is the y-intercept Point-Slope Form • Use this form when you know a point on the line and the slope • Also can use this version if you have two points on the line because you can first find the slope using the slope formula and then use one of the points and the slope in this equation. General Form • Commonly used to write linear equation problems or express answers

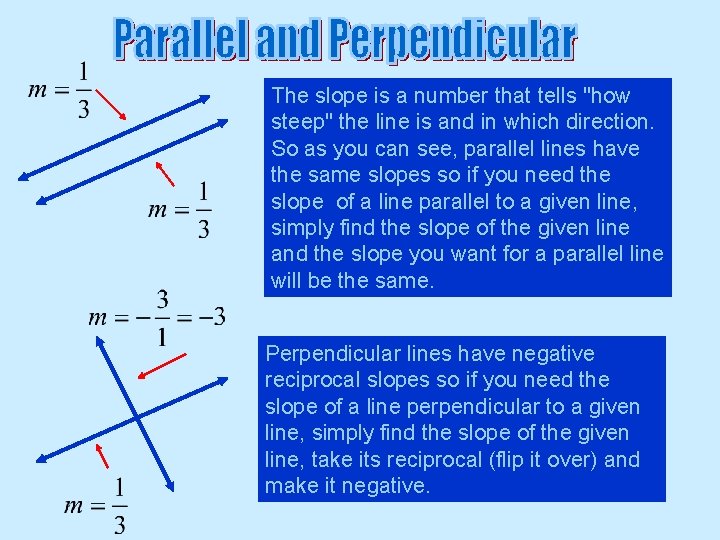
The slope is a number that tells "how steep" the line is and in which direction. So as you can see, parallel lines have the same slopes so if you need the slope of a line parallel to a given line, simply find the slope of the given line and the slope you want for a parallel line will be the same. Perpendicular lines have negative reciprocal slopes so if you need the slope of a line perpendicular to a given line, simply find the slope of the given line, take its reciprocal (flip it over) and make it negative.

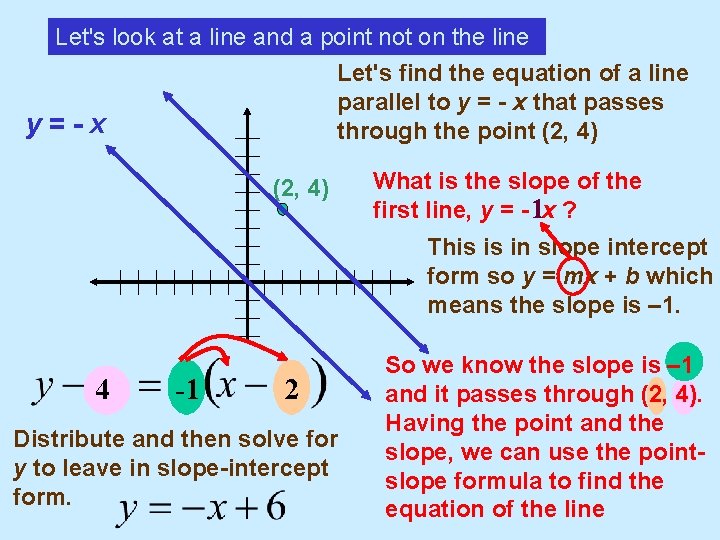
Let's look at a line and a point not on the line Let's find the equation of a line parallel to y = - x that passes y=-x through the point (2, 4) What is the slope of the first line, y = - 1 x ? This is in slope intercept form so y = mx + b which means the slope is – 1. 4 -1 2 Distribute and then solve for y to leave in slope-intercept form. So we know the slope is – 1 and it passes through (2, 4). Having the point and the slope, we can use the pointslope formula to find the equation of the line

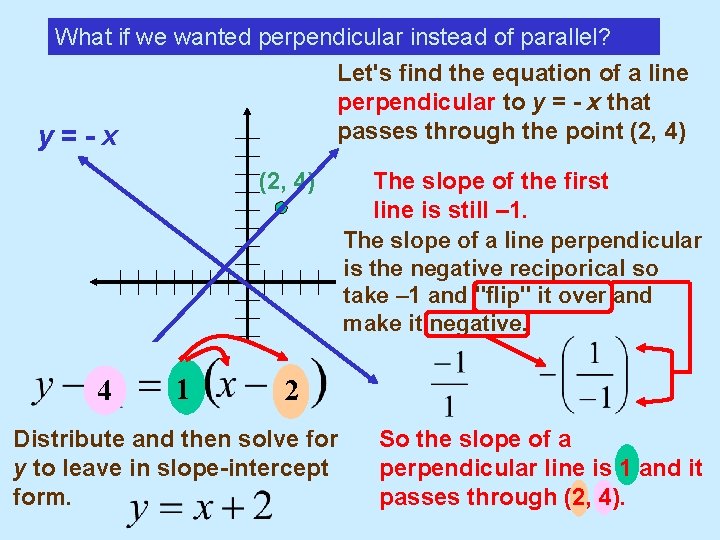
What if we wanted perpendicular instead of parallel? Let's find the equation of a line perpendicular to y = - x that passes through the point (2, 4) y=-x (2, 4) 4 1 The slope of the first line is still – 1. The slope of a line perpendicular is the negative reciporical so take – 1 and "flip" it over and make it negative. 2 Distribute and then solve for y to leave in slope-intercept form. So the slope of a perpendicular line is 1 and it passes through (2, 4).