Lesson 3 2 Angles Parallel Lines TARGETS Use







- Slides: 15

Lesson 3 -2: Angles & Parallel Lines TARGETS • Use theorems to determine the relationships between specific pairs of angles. • Use algebra to find angle measurements.

Content Standards G-CO. 1 Experiment with transformations in the plane. G-CO. 9 Prove geometric theorems. G-CO. 12 Make geometric constructions. Mathematical Practices 2 Reason abstractly and quantitatively. 6 Attend to precision.

LESSON 3 -2: Angles & Parallel Lines What is a Postulate? Describes a fundamental relationship between the basic terms of geometry Accepted to be true without proof

LESSON 3 -2: Angles & Parallel Lines What is a Theorem? A statement or conjecture that can be proven true by undefined terms, definitions and postulates.

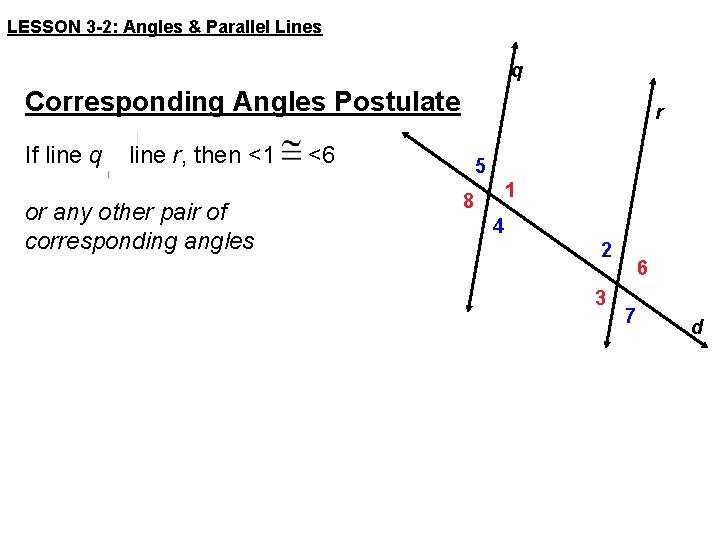
LESSON 3 -2: Angles & Parallel Lines q Corresponding Angles Postulate If line q line r, then <1 or any other pair of corresponding angles r <6 5 1 8 4 2 3 6 7 d

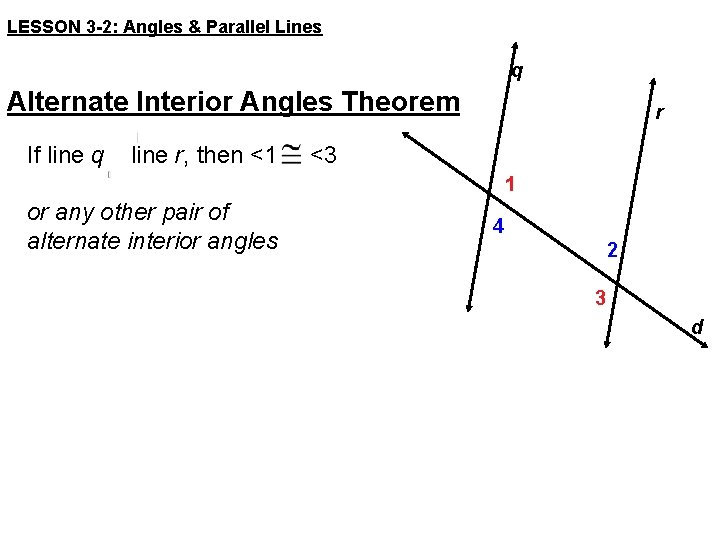
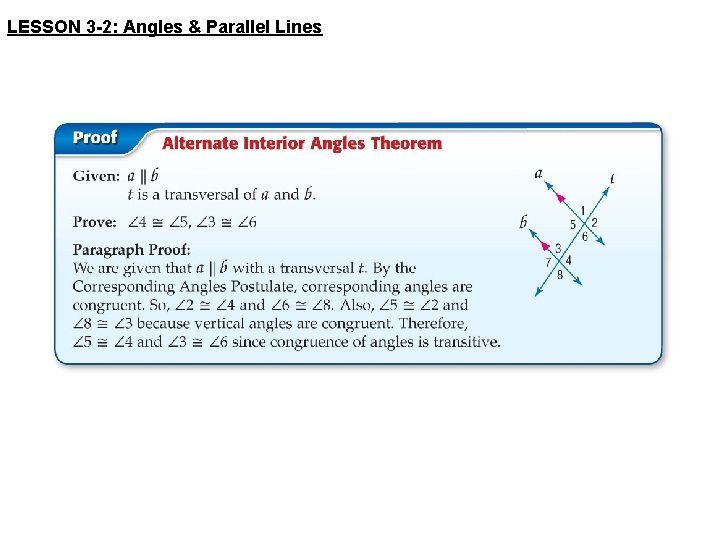
LESSON 3 -2: Angles & Parallel Lines q Alternate Interior Angles Theorem If line q line r, then <1 r <3 1 or any other pair of alternate interior angles 4 2 3 d

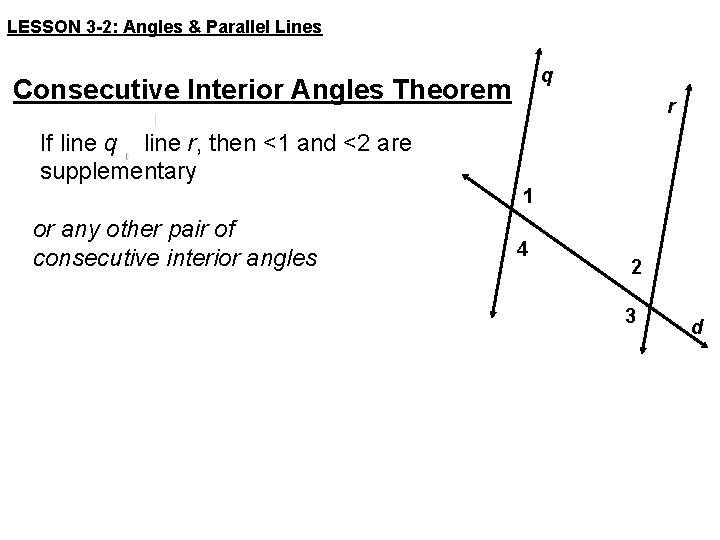
LESSON 3 -2: Angles & Parallel Lines q Consecutive Interior Angles Theorem r If line q line r, then <1 and <2 are supplementary 1 or any other pair of consecutive interior angles 4 2 3 d

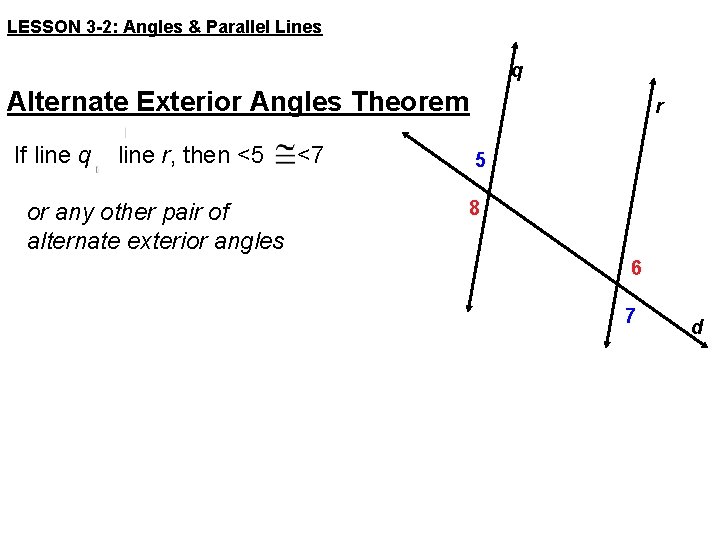
LESSON 3 -2: Angles & Parallel Lines q Alternate Exterior Angles Theorem If line q line r, then <5 or any other pair of alternate exterior angles <7 r 5 8 6 7 d

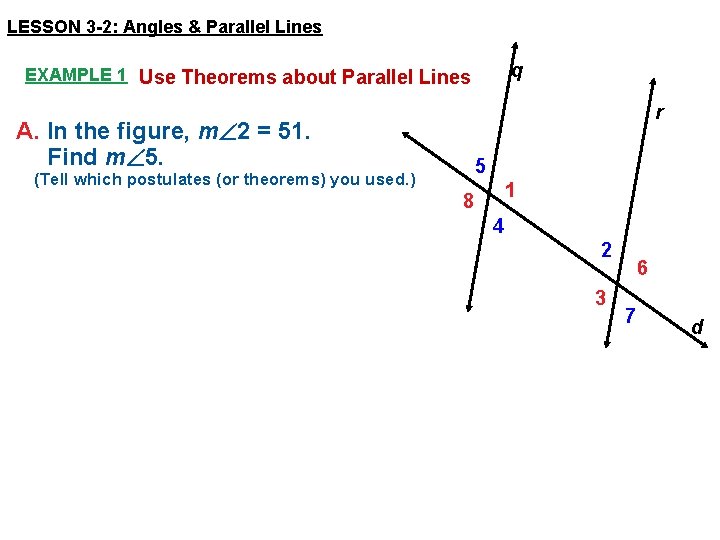
LESSON 3 -2: Angles & Parallel Lines q EXAMPLE 1 Use Theorems about Parallel Lines r A. In the figure, m 2 = 51. Find m 5. 5 (Tell which postulates (or theorems) you used. ) 1 8 4 2 3 6 7 d

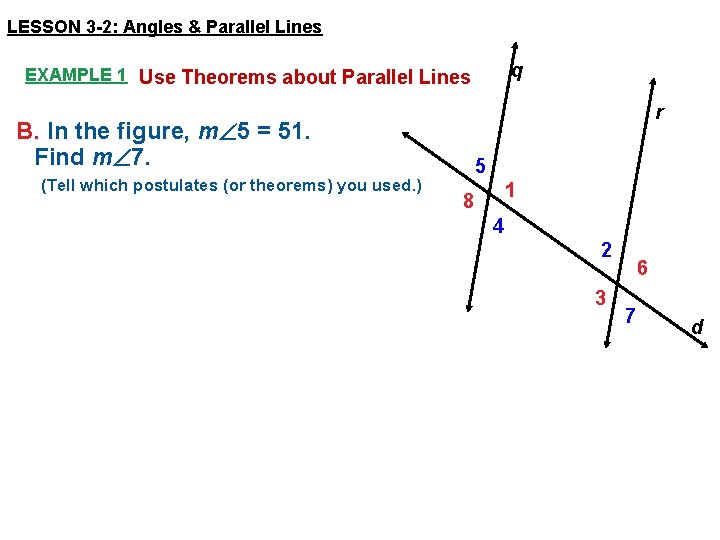
LESSON 3 -2: Angles & Parallel Lines q EXAMPLE 1 Use Theorems about Parallel Lines r B. In the figure, m 5 = 51. Find m 7. (Tell which postulates (or theorems) you used. ) 5 1 8 4 2 3 6 7 d

LESSON 3 -2: Angles & Parallel Lines EXAMPLE 2 Use Theorems about Parallel Lines FLOOR TILES The diagram represents the floor tiles in Michelle’s house. If m 2 = 125, find m 3. 2 3 m 2 = m 3 125 = m 3 Alternate Interior Angles Postulate Definition of congruent angles Substitution Answer: m 3 = 125

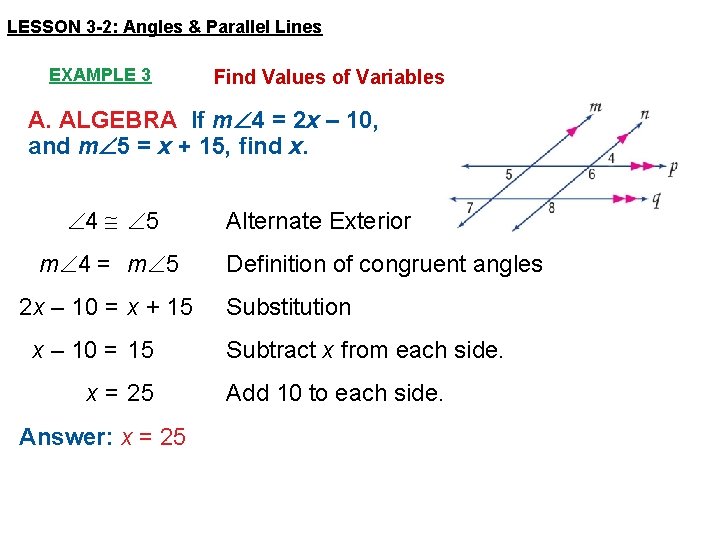
LESSON 3 -2: Angles & Parallel Lines EXAMPLE 3 Find Values of Variables A. ALGEBRA If m 4 = 2 x – 10, and m 5 = x + 15, find x. 4 5 m 4 = m 5 2 x – 10 = x + 15 x – 10 = 15 x = 25 Answer: x = 25 Alternate Exterior Definition of congruent angles Substitution Subtract x from each side. Add 10 to each side.

LESSON 3 -2: Angles & Parallel Lines EXAMPLE 3 Find Values of Variables B. ALGEBRA If m 4 = 4(y – 25), and m 8 = 4 y, find y. 8 6 Corresponding Angles Postulate m 8 = m 6 Definition of congruent angles 4 y = m 6 Substitution m 6 + m 4 = 180 4 y + 4(y – 25)= 180 4 y + 4 y – 100 = 180 Supplement Theorem Substitution Distributive Property 8 y = 280 Add 100 to each side. y = 35 Divide each side by 8. Answer: y = 35

LESSON 3 -2: Angles & Parallel Lines

LESSON 3 -2: Angles & Parallel Lines Perpendicular Transversal Theorem If line a line b and line a line t, then line b line t.
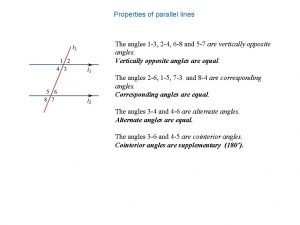
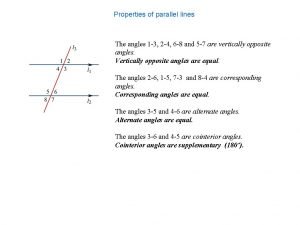
 Congruent angles on parallel lines
Congruent angles on parallel lines How to tell if two lines are parallel geometry
How to tell if two lines are parallel geometry Properties of vertically opposite angles
Properties of vertically opposite angles Properties of parallel lines 3-2
Properties of parallel lines 3-2 3-2 properties of parallel lines
3-2 properties of parallel lines Angles formed by parallel lines
Angles formed by parallel lines Transversal vocabulary
Transversal vocabulary Parallel lines
Parallel lines Adjacent in geometry
Adjacent in geometry Parallel lines angle property
Parallel lines angle property Pre algebra angles
Pre algebra angles 14-2 transversals and parallel lines answer key
14-2 transversals and parallel lines answer key Coinciding lines
Coinciding lines Quiz 3-1 parallel lines transversals and angles
Quiz 3-1 parallel lines transversals and angles Use parallel lines and transversals assignment
Use parallel lines and transversals assignment 3-2 angles formed by parallel lines and transversals
3-2 angles formed by parallel lines and transversals