Slopes of Parallel and Perpendicular Lines Objective To

Slopes of Parallel and Perpendicular Lines Objective: To discover the relationships between the slopes of parallel lines and perpendicular lines.

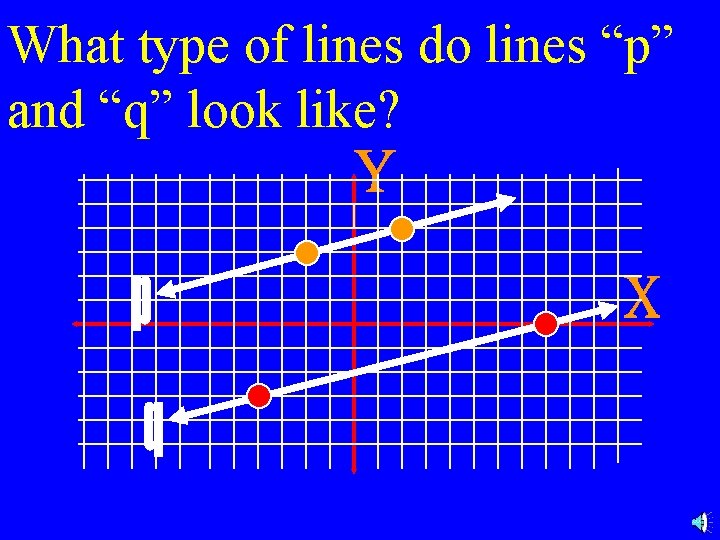
What type of lines do lines “p” and “q” look like?

Answer p and q appear to be parallel lines! How can we use mathematics to be sure they are indeed parallel?

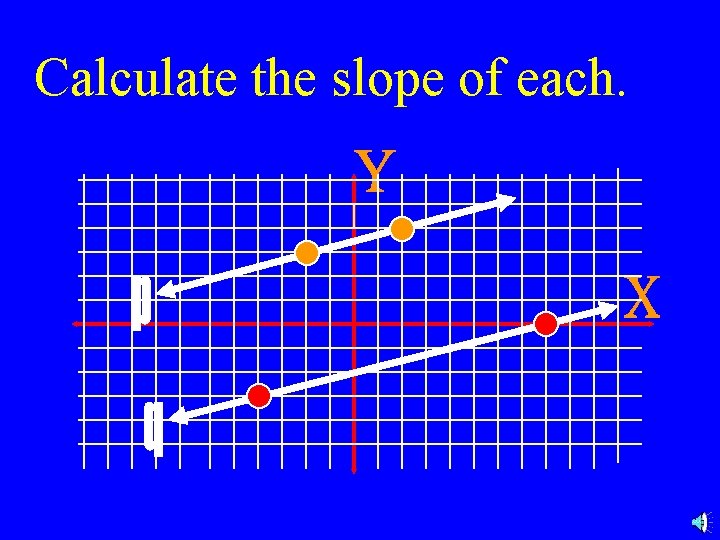
Calculate the slope of each.

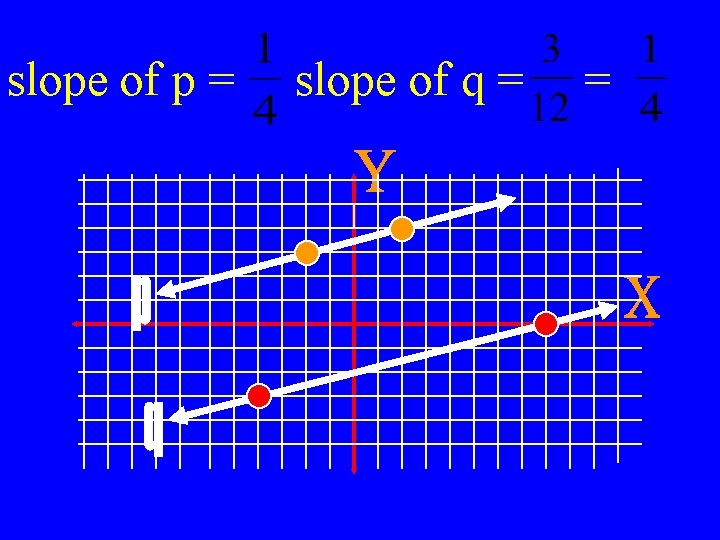
slope of p = slope of q = =

What do you notice about the slopes of these two lines? • The slopes are congruent. parallel congruent

Parallel Conjucture: • Two lines are parallel if their slopes are equal. • Recall the definition of parallel lines then write a few sentences describing why it makes sense that parallel lines would have equal slopes.

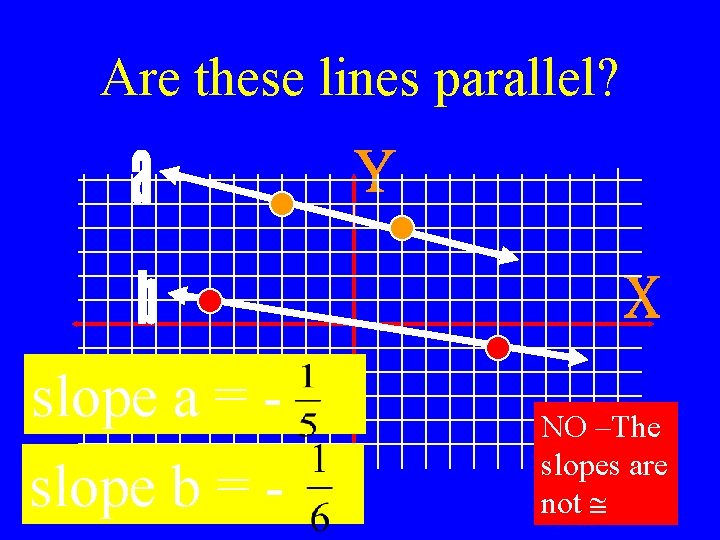
Are these lines parallel? slope a = slope b = - NO –The slopes are not

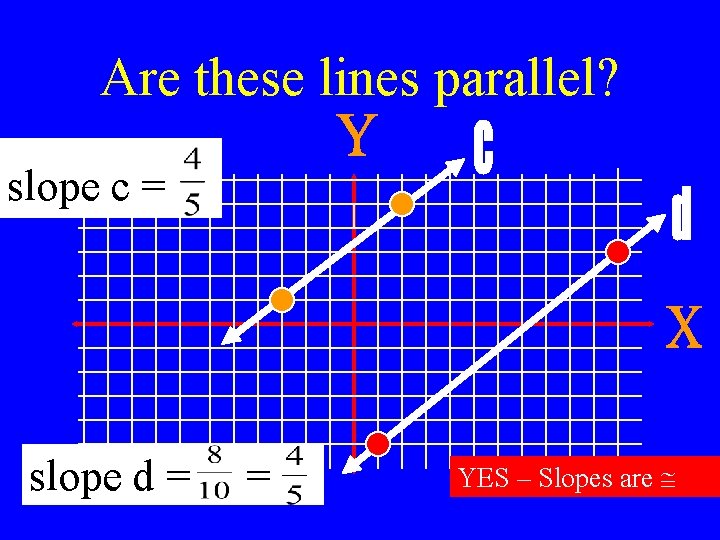
Are these lines parallel? slope c = slope d = = YES – Slopes are

You will be shown the slopes of two lines. Write down whether each pair of lines are parallel or not.

1. slope of line r = slope of line s = These lines are parallel.

3. slope of line t = slope of line u = These lines are parallel.

4. slope of line t = slope of line u = Not parallel because the slopes are not congruent to each other.

Ex. Determine whether the graphs of y = -3 x + 4 and 6 x + 2 y = -10 are parallel lines. Step 1: make both equations in the y-intercept form to compare slopes 6 x + 2 y = -10 can be changed to y-intercept form by solving for y

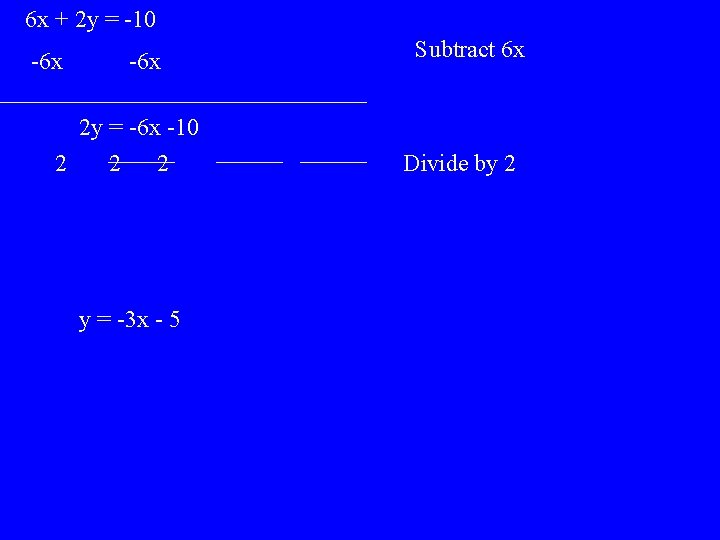
6 x + 2 y = -10 -6 x Subtract 6 x 2 y = -6 x -10 2 2 2 y = -3 x - 5 Divide by 2

Step 2: compare the slopes of both equations. The first equation y = -3 x + 4 has a slope of -3 and the second equation has the same slope of -3 Therefore, the graph of the lines will be parallel.

Practice: Determine whether the graphs are parallel lines (without graphing) 1) 3 x - y = -5 and 5 y -15 x = 10 2) 4 y = -12 x + 16 and y = 3 x + 4