Properties of parallel lines The angles 1 3

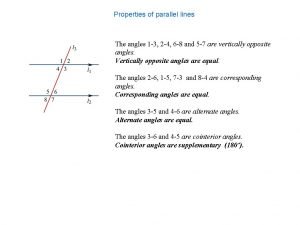
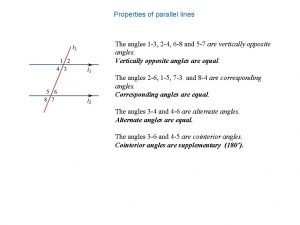
Properties of parallel lines The angles 1 -3, 2 -4, 6 -8 and 5 -7 are vertically opposite angles. Vertically opposite angles are equal. The angles 2 -6, 1 -5, 7 -3 and 8 -4 are corresponding angles. Corresponding angles are equal. The angles 3 -4 and 4 -6 are alternate angles. Alternate angles are equal. The angles 3 -6 and 4 -5 are cointerior angles. Cointerior angles are supplementary (180∘).

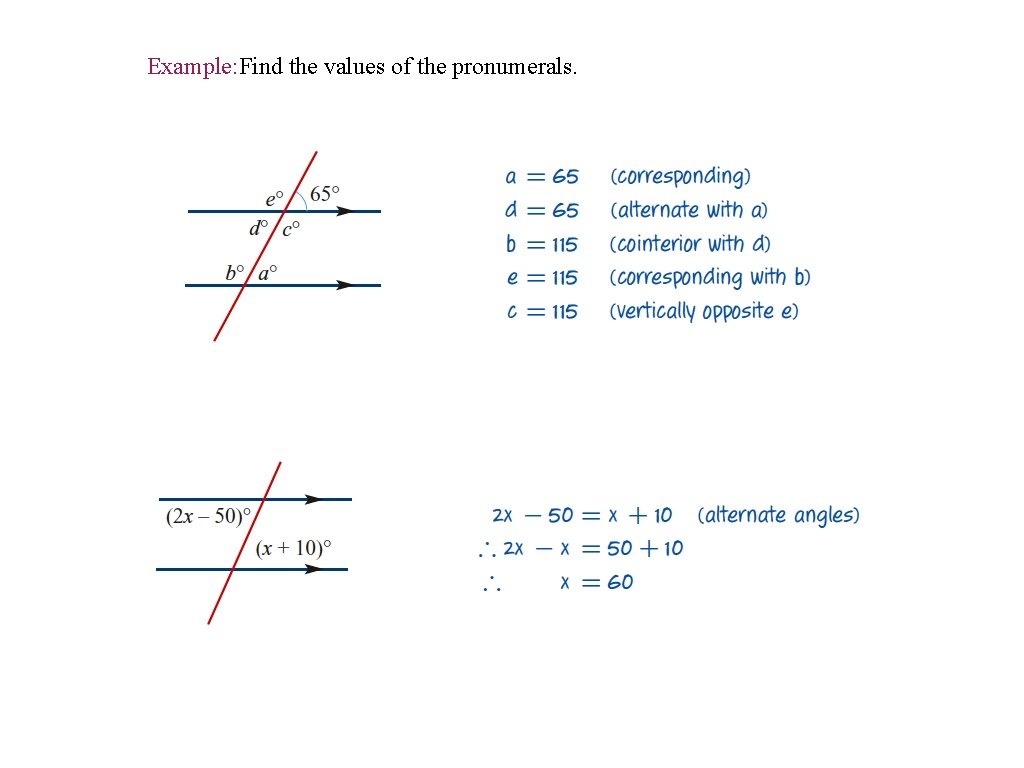
Example: Find the values of the pronumerals.

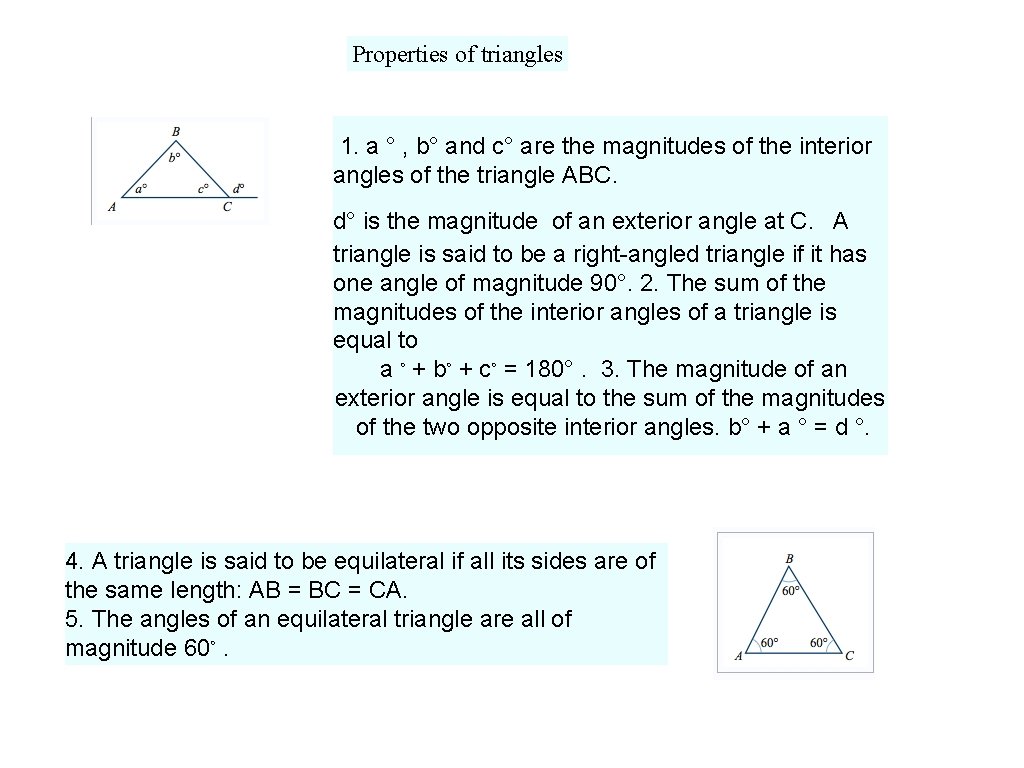
Properties of triangles 1. a ° , b° and c° are the magnitudes of the interior angles of the triangle ABC. d° is the magnitude of an exterior angle at C. A triangle is said to be a right-angled triangle if it has one angle of magnitude 90°. 2. The sum of the magnitudes of the interior angles of a triangle is equal to a ◦ + b◦ + c◦ = 180°. 3. The magnitude of an exterior angle is equal to the sum of the magnitudes of the two opposite interior angles. b° + a ° = d °. 4. A triangle is said to be equilateral if all its sides are of the same length: AB = BC = CA. 5. The angles of an equilateral triangle are all of magnitude 60◦.

6. The bisector of each of the angles of an equilateral triangle meets the opposite side at right angles and passes through the midpoint of that side. 7. A triangle is said to be isosceles if it has two sides of equal length. If a triangle is isosceles, the angles opposite each of the equal sides are equal. 8. The sum of the magnitudes of the exterior angles of a triangle is equal to 360°: e° +d°+f°=360° Example 1: Find the values of the pronumerals. Solution: 20° +22°+x°=180° (sum angles△=180°) ∴ 42° +x°=180° or x =138°+y°=180° (sum angles=180°) ∴y =42°

Example: Find the values of the pronumerals. Solution: 100°+2 x°=180° (sum angles△=180°) ∴ 2 x° =80° or x =40°

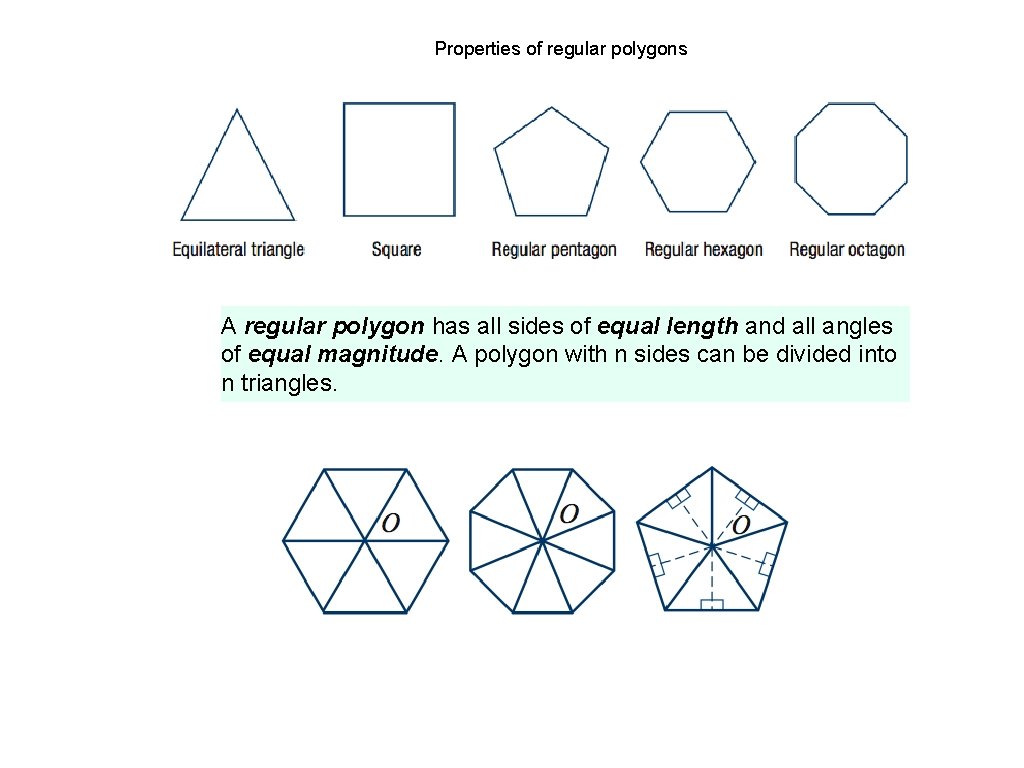
Properties of regular polygons A regular polygon has all sides of equal length and all angles of equal magnitude. A polygon with n sides can be divided into n triangles.

The angle sum of the interior angles of an n-sided polygon is given by the formula: S = [180(n − 2)]◦ = (180 n − 360)◦ The magnitude of each of the interior angles of an n-sided polygon is given by: x = (180 n − 360)◦ n interior angle exterior angle The sum of the exterior angles of a regular polygon is 360◦. Example 1: The diagram opposite shows a regular octagon. a Show that x = 45. b Find the size of angle y. Solution a x = 360°÷ 8 = 45° b BOC is isosceles ∧ ∧ then OBC and OCB are equal x° + 2 y°= 180° 45° + 2 y° = 180° 2 y°= 180° - 45° 2 y°= 135° y° = 67. 5°

Example: Find the sum of the interior angles of an 8 -sided polygon(octagon). Solution Use the formula x°= (180 n-360)° x°= 180× 8 -360 = 1080 ° Pythagoras theorem Example 1: Find the value, correct to two decimal places, of the unknown length for the triangle below. Solution: x 2 = 5. 32 + 6. 12 √x 2 = √( 5. 32 + 6. 12) x = 8. 08 cm

Example 2: Find the value, correct to two decimal places, of the unknown length for the triangle below. Solution: 8. 62 = y 2 + 5. 62 y 2 = 8. 62 - 5. 62 y = √( 8. 62 - 5. 62) y = 6. 53 cm Similar figures Shapes are similar when they have the same shape but not the same size.

Similar Triangles Two triangles are similar if one of the following conditions holds: 1. The corresponding angles in the triangles are equal A = A′, B = B′, C = C′ 2. The ratio of the corresponding sides is equal A′B′ = B′C′ = A′C′ =k AB BC AC k is the scale factor. If AB = 2, BC = 3, AC =4 and A′B′ = 6, B′C′ = 9, A′C′= 12 then 6 = 9 = 12 = 3= k 2 3 4 3. Two pairs of corresponding sides have the same ratio and the included angles are equal

Example 1: Find the value of length of side AC in △ABC, correct to two decimal places. Solution: Prove that the triangles are similar. B= B′ and 5 = 4 3 =4 6. 25 5 3. 75 5 k=4 5 (Two pairs of corresponding sides of equal ratio and the included angles equal). Use k to find x x =5 3. 013 6. 25 x = 3. 013 x 5 = 2. 4103 ≈2. 41 cm 6. 25

Example 2: Find the value of length of side AB in △ABC. Solution: Prove that the triangles ACB and AYX are similar. A is a common angle ∧ ∧ C=Y ( corresponding angles) ∧ ∧ B=X ( corresponding angles) Use the ratio to find x x = 3 x + 6 3+ 2. 5 x = 3 x+6 5. 5 x = 3(x + 6) 5. 5 x = 3 x + 18 2. 5 x = 18 2. 5 x = 7. 2 cm cross multiply

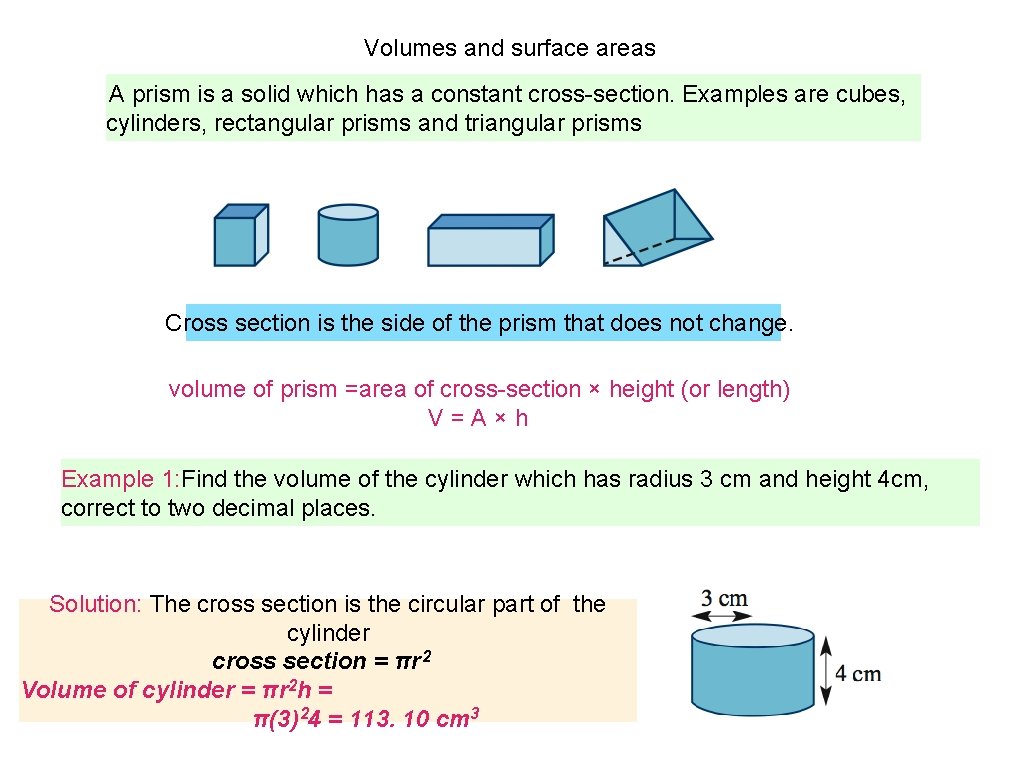
Volumes and surface areas A prism is a solid which has a constant cross-section. Examples are cubes, cylinders, rectangular prisms and triangular prisms Cross section is the side of the prism that does not change. volume of prism =area of cross-section × height (or length) V=A×h Example 1: Find the volume of the cylinder which has radius 3 cm and height 4 cm, correct to two decimal places. Solution: The cross section is the circular part of the cylinder cross section = πr 2 Volume of cylinder = πr 2 h = π(3) 24 = 113. 10 cm 3

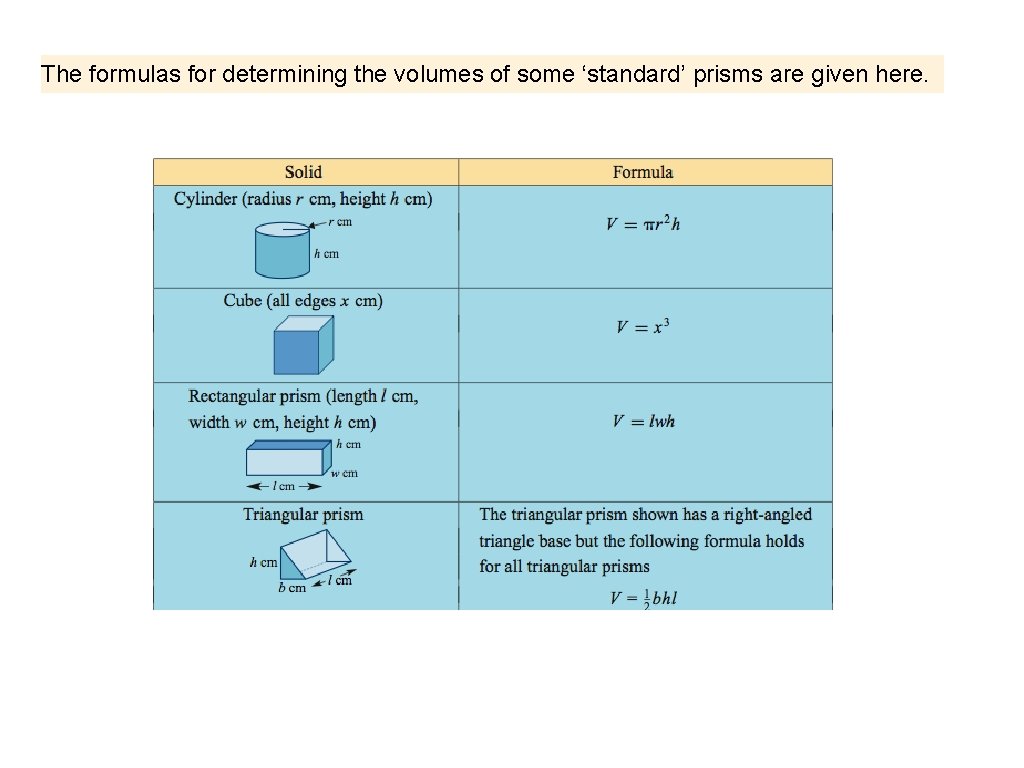
The formulas for determining the volumes of some ‘standard’ prisms are given here.

Volume of a pyramid Pyramids are shapes where the outer surfaces are triangular and converge at a point. The base of the pyramid can be square, triangular. . . Volume of pyramid = 1 × base area × perpendicular height 3 For the square pyramid shown: V = 1 x 2 h 3 Example: Find the volume of this hexagonal pyramid with a base area of 40 cm 2 and a height of 20 cm. Give the answer correct to one decimal place. Solution V = 1 ×A×h = 1 × 40× 20 =266. 7 cm 3 3 3

Example: Find the volume of this square pyramid with a square base with each edge 10 cm and a height of 27 cm. Solution V = 1 ×A×h = 1 × 10 x 27 = 900 cm 3 3 3 Volume of cone Cones are shapes where the outer surfaces are rounded and converge at a point. The base of the cone is circular. The formula for finding the volume of a cone can be stated as: Volume of cone = 1 × base area × height 3 Volume of cone = 1 × π r 2 × height 3

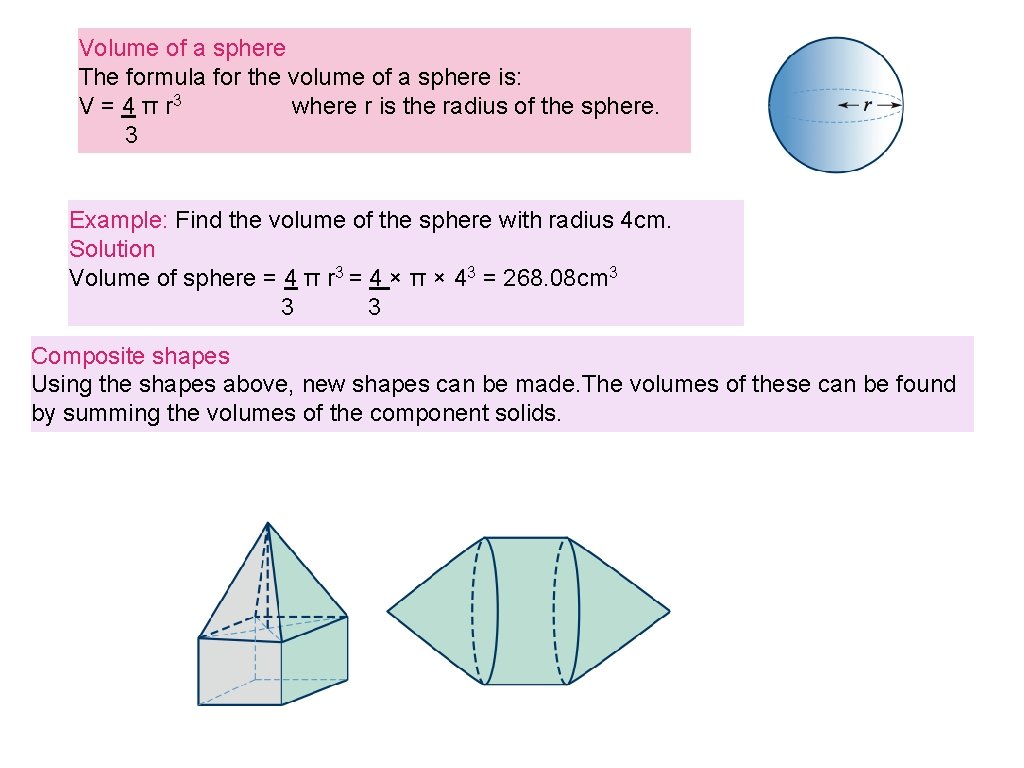
Volume of a sphere The formula for the volume of a sphere is: V = 4 π r 3 where r is the radius of the sphere. 3 Example: Find the volume of the sphere with radius 4 cm. Solution Volume of sphere = 4 π r 3 = 4 × π × 43 = 268. 08 cm 3 3 3 Composite shapes Using the shapes above, new shapes can be made. The volumes of these can be found by summing the volumes of the component solids.

Example: A hemisphere is placed on top of a cylinder to form a capsule. The radius of both the hemisphere and the cylinder is 5 mm. The height of the cylinder is also 5 mm. What is the volume of the composite solid in cubic millimeters, cor rect to two decimal places? Solution: Volume of the composite = volume of cylinder+volume of hemisphere = π r 2 h + 1 (4 π r 3) 2 3 = π 5 2 × 5 + 1 (4 π 53) 2 3 = 654. 50 mm 3

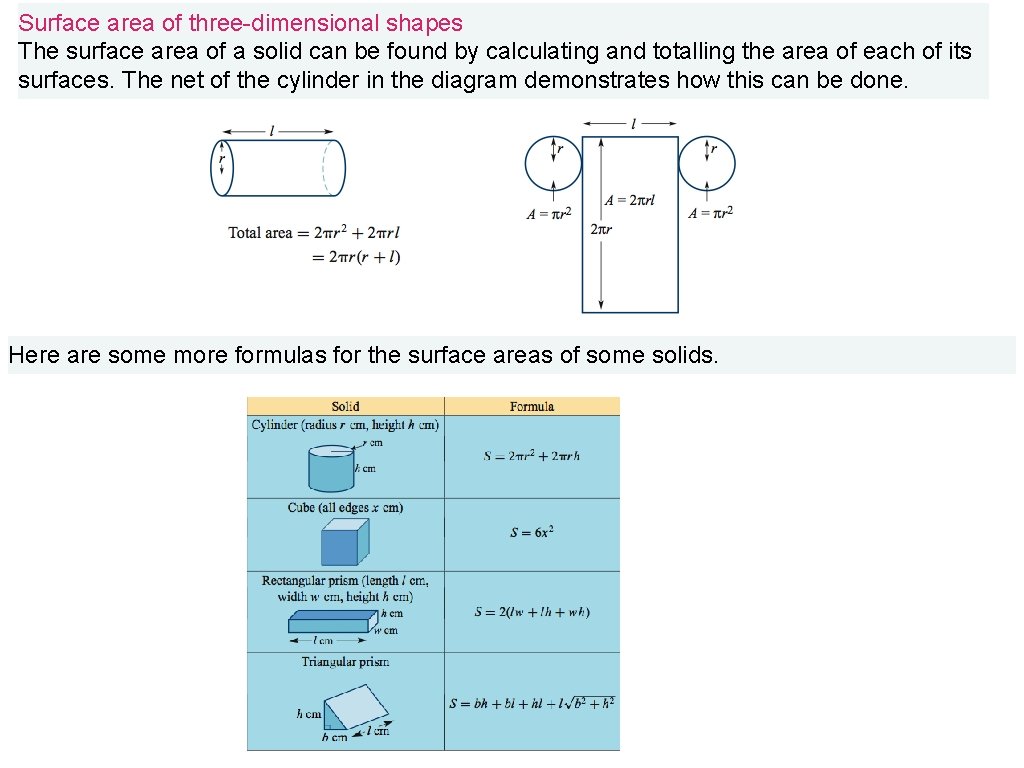
Surface area of three-dimensional shapes The surface area of a solid can be found by calculating and totalling the area of each of its surfaces. The net of the cylinder in the diagram demonstrates how this can be done. Here are some more formulas for the surface areas of some solids.

Example: Find the surface of the right square pyramid shown if the square base has each edge 10 cm in length and the isosceles triangles each have height 15 cm. Solution: TSA = 4 × 1 10 × 15 + 10 × 10 = 300 + 100 = 400 cm 2 2 Lengths, Areas, Volumes and Similarity Definition 1: When two shapes are similar the ratio of their sides is k. where k = scale factor Ratio of lengths = length 1 =3 = k length 2 4

Definition 2: When two shapes are similar the ratio of their areas is k 2. Ratio of areas = area 1 = π× 32=(3)2 = 9 =k 2 area 2 π× 42 (4)2 16 Definition 3: When two shapes are similar the ratio of their volumes is k 3. Ratio of volumes = of volume 1= 4/3π× 33 = (3)3 = 27 =k 3 of volume 2 4/3π× 43 (4)3 64 Example 1: The two triangles shown are similar. The base of the smaller triangle has a length of 10 cm. Its area is 40 cm 2. The base of the larger triangle has a length of 25 cm. Determine its area. Solution: Ratio of lengths = length small = 10 = 2 = k length big 25 5 k 2 = 4 1 25 Ratio of areas = k 2 = 40 2 x 1=2 and 4 = 40 25 x x = 25 × 40 = 250 cm 2 4

Example 2: The two cuboids shown are similar solids. The height of the larger cuboid is 6 cm. Its volume is 120 cm 3. The height of the smaller cuboid is 1. 5 cm. Determine its volume. Solution: Ratio of lengths = length small = 1. 5 = 1 = k length big 6 4 k 3 = 1 1 64 Ratio of volume= k 3 = x 2 120 1=2 and 1 = x 64 120 x = 120 = 1. 875 cm 3 64

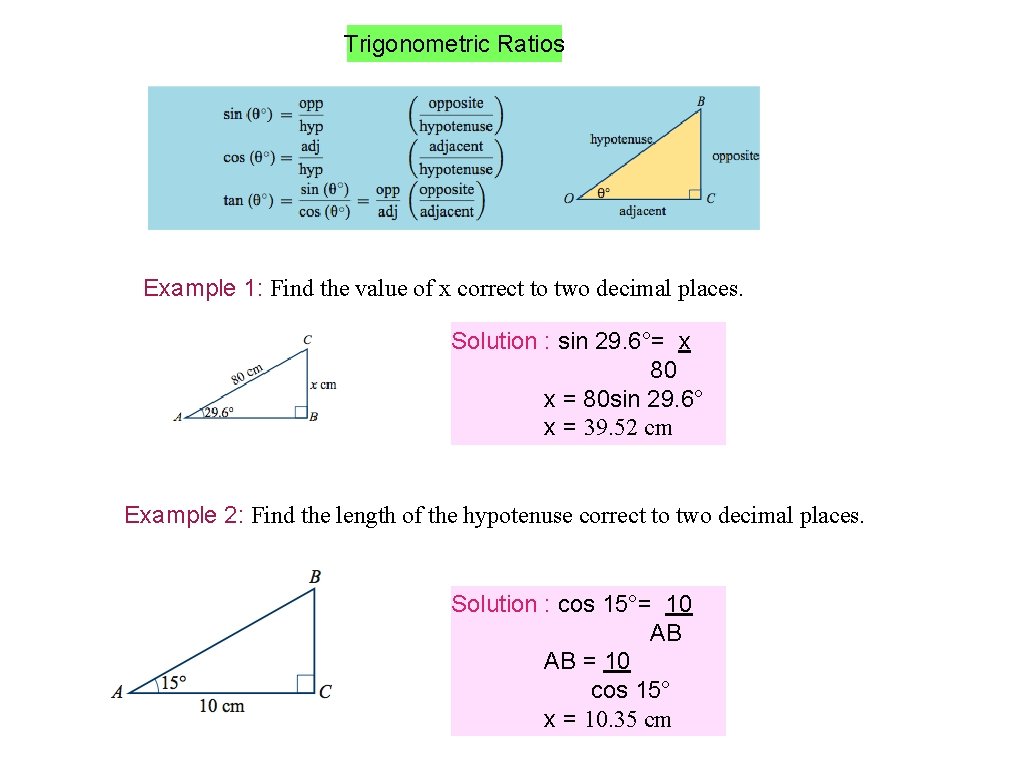
Trigonometric Ratios Example 1: Find the value of x correct to two decimal places. Solution : sin 29. 6°= x 80 x = 80 sin 29. 6° x = 39. 52 cm Example 2: Find the length of the hypotenuse correct to two decimal places. Solution : cos 15°= 10 AB AB = 10 cos 15° x = 10. 35 cm

Example 3: Find the magnitude of ∠ABC. tan x° = 11 3 x° = tan-1 11 3 x°= 74. 74° When the triangles are not right-angled then the pythagoras theorem and the trigonometric ratios are not appropriate for finding unknown lenghts and angles. The appropriate rules to use are the sine rule and the cosine rule. The sine rule We use the sine rule when we are given: 1. Two sides and the non- included angle 2. One side and two angles Considering that the lower- case letters represent the sides of the triangle and the upper- case represent angles, then the following formula states the sine rule. a = b = c sin. A sin. B sin. C

The cosine rule We use the cosine rule when is given: 1. Two sides and the included angle of the triangle. 2. All sides.

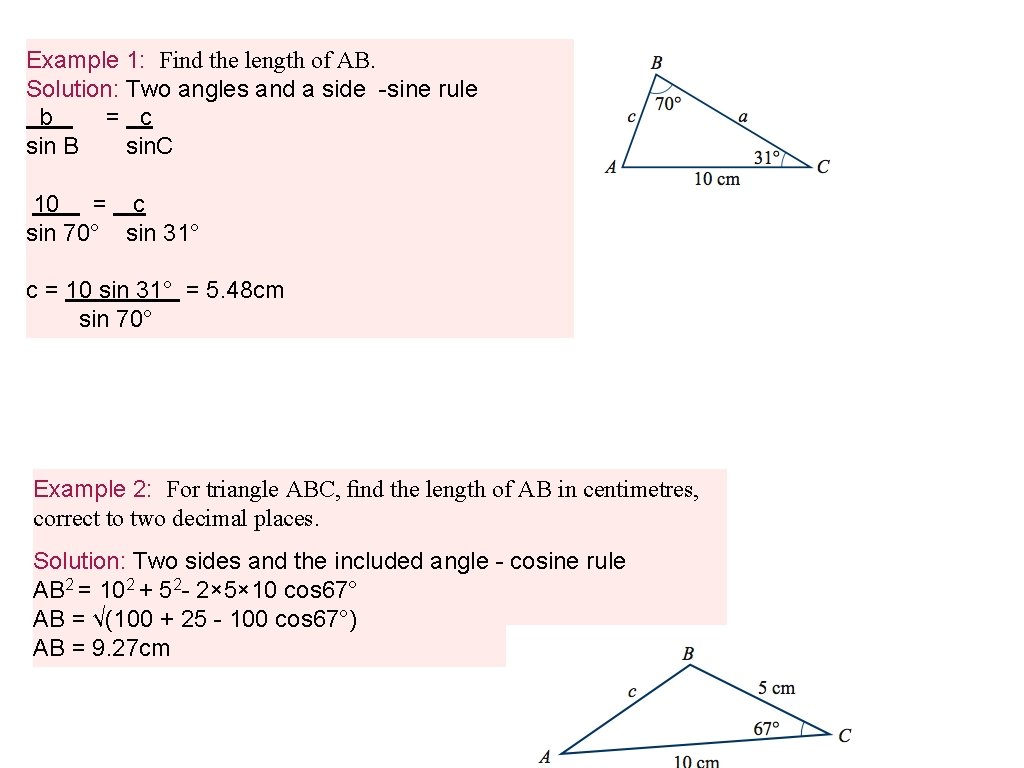
Example 1: Find the length of AB. Solution: Two angles and a side -sine rule b = c sin B sin. C 10 = c sin 70° sin 31° c = 10 sin 31° = 5. 48 cm sin 70° Example 2: For triangle ABC, find the length of AB in centimetres, correct to two decimal places. Solution: Two sides and the included angle - cosine rule AB 2 = 102 + 52 - 2× 5× 10 cos 67° AB = √(100 + 25 - 100 cos 67°) AB = 9. 27 cm

Example 3: Find the magnitude of angle B. Solution: Three sides- cosine rule cos. B = 62 + 122 - 152 2× 6× 12 B = cos-1(62 + 122 - 152) 2× 6× 12 B =cos-1(-45/144) = 108. 21° Area of the triangle It is known that the area of a triangle is given by the formula Area = 1 × base length ×height 2 A = 1 bh 2

When the triangle is not a right angled and the 2 sides and the included angle is given the following formula can be used A = 1 × side a × side b × sin (angle in between a and b) 2 Example 1: Find the area of triangle ABC. Give your answer correct to two decimal places. Solution: The triangle is not right angled and we are given 2 sides and the included angle. We can use the formula A =1/2 ac sin. B A= 1/2 × 6. 5 × 7. 2 × sin 140° = 15. 04°

Heron’s Formula When the 3 sides of the triangle are given, then Heron’s Formula can be used to determine the area of the triangle: Example 1: Find the area of the triangle with sides 6 cm, 4 cm and 4 cm. Give your answer correct to two decimal places. Solution: s = (6+4+4) = 7 2 A = √ 7(7 - 6)(7 - 4) = √ 7 × 1 × 3 = √ 63 = 7. 94 cm 2

Angles of elevation and depression The angle of elevation is the angle between the horizontal and a direction above the horizontal. The angle of depression is the angle between the horizontal and a direction below the horizontal. Example 1: The pilot of a helicopter flying at 400 m observes a small boat at an angle of depression of 1. 2◦. Draw a diagram and calculate the horizontal distance of the boat to the helicopter, correct to the nearest 10 metres. Solution: The horizontal distance of the boat to the helicopter is AB. The angle of depression H = B ( alternate). tan(1. 2◦) = 400 AB AB = 400 tan(1. 2◦) AB = 19 095. 80 m

Example 2: The light on a cliff-top lighthouse, known to be 75 m above sea level, is observed from a boat at an angle of elevation of 7. 1◦. Draw a diagram and calculate the distance of the boat from the lighthouse, to the nearest metre. Solution: tan (7. 1◦) = 75 AB AB = 75 tan (7. 1◦) AB = 602 m Example 3: From a point A, a man observes that the angle of elevation of the summit of a hill is 10◦. He then walks towards the hill for 500 m along flat ground. The summit of the hill is now at an angle of elevation of 14◦. Draw a diagram and find the height of the hill above the level of A, to the nearest metre. Solution: We need to find HC To find HC we need to find HB 3 angles and a side are given- sine rule HB = 500 sin(10◦) sin(4◦) HB = 500 sin(10◦) = 1244. 67 m sin(4◦) sin(14◦) = HC 1244. 67 HC = 1244. 67 sin(14◦) = 301. 11 m

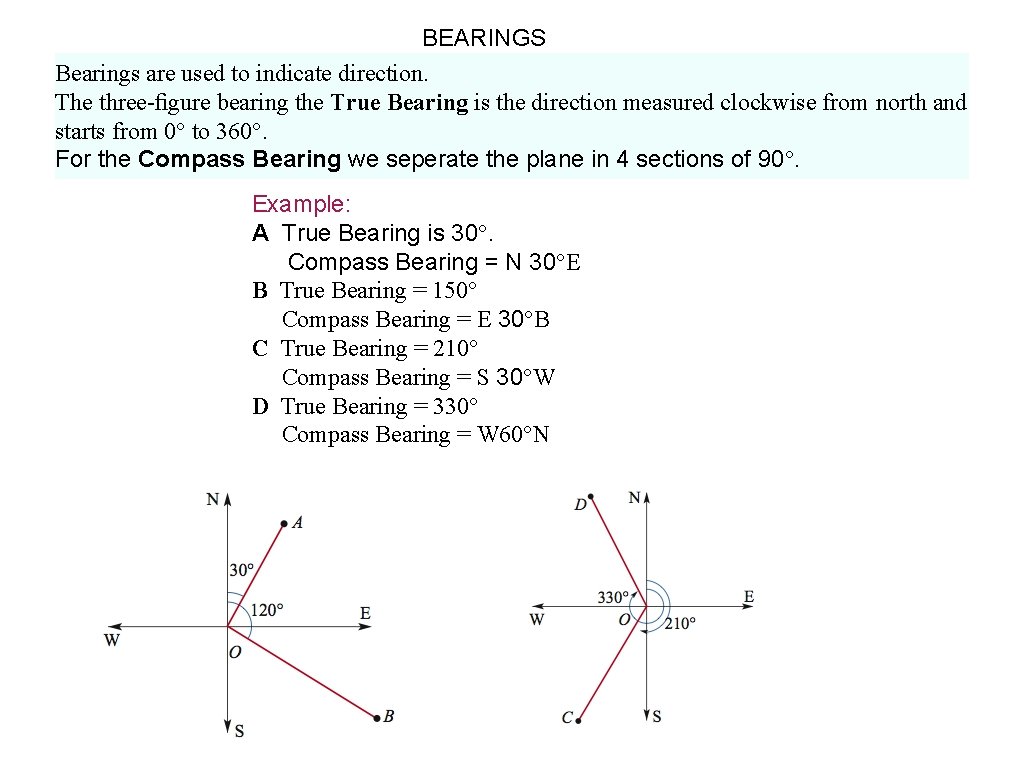
BEARINGS Bearings are used to indicate direction. The three-figure bearing the True Bearing is the direction measured clockwise from north and starts from 0° to 360°. For the Compass Bearing we seperate the plane in 4 sections of 90°. Example: A True Bearing is 30°. Compass Bearing = N 30°E B True Bearing = 150° Compass Bearing = E 30°B C True Bearing = 210° Compass Bearing = S 30°W D True Bearing = 330° Compass Bearing = W 60°N

Example: The road from town A runs due west for 14 km to town B. A television mast is located due south of B at a distance of 23 km. Draw a diagram and calculate the distance of the mast from the centre of town A, to the nearest kilometre. Find the bearing of the mast from the centre of the town. Solution: AT 2 = 142 + 232 AT = √( 142 + 232 ) = 26. 93 km For Bearing find θ tan θ = 23 14 θ = tan-1(23/14) = 58. 67° Bearing = 270°- 58. 67°= 211. 33° The bearing of the mast from A is 211. 33°T

Example: A yacht starts from a point A and sails on a bearing of 038◦ for 3000 m. It then alters its course to a bearing of 318◦, and after sailing for 3300 m it reaches a point B. a Find the distance AB, correct to the nearest metre. b Find the bearing of B from A, correct to the nearest degree. Solution: a 2 sides and the included angle are givencosine rule AB = √(33002 +30002 - 2 × 3300 × 3000 cos 100°) AB = 4830 m b To find the bearing of B from A we need to find angle A We may use sine and cosine rule 3300 = 4830 sin. A° sin 100° A°= sin-1 (3300 sin 100° ) = 42. 28° 4830 The bearing of B from A = 360◦ −(42. 29◦- 38◦ ) = 355. 71◦ The bearing of B from A is 356◦T , to the nearest degree.

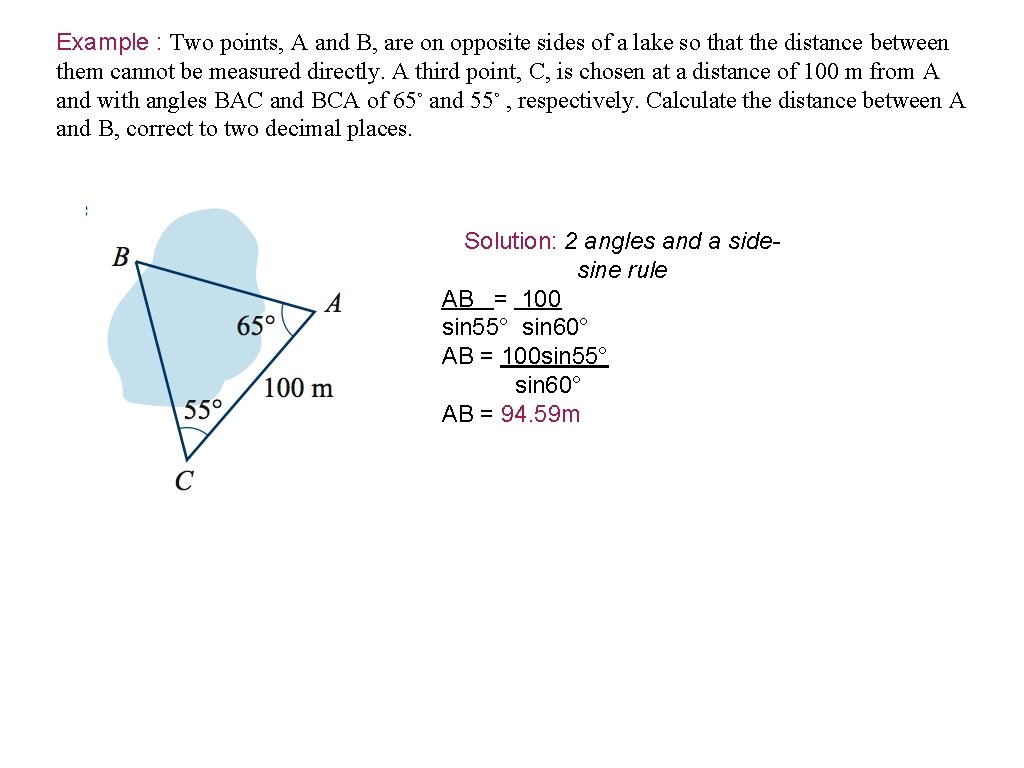
Example : Two points, A and B, are on opposite sides of a lake so that the distance between them cannot be measured directly. A third point, C, is chosen at a distance of 100 m from A and with angles BAC and BCA of 65◦ and 55◦ , respectively. Calculate the distance between A and B, correct to two decimal places. Solution: 2 angles and a sidesine rule AB = 100 sin 55° sin 60° AB = 100 sin 55° sin 60° AB = 94. 59 m

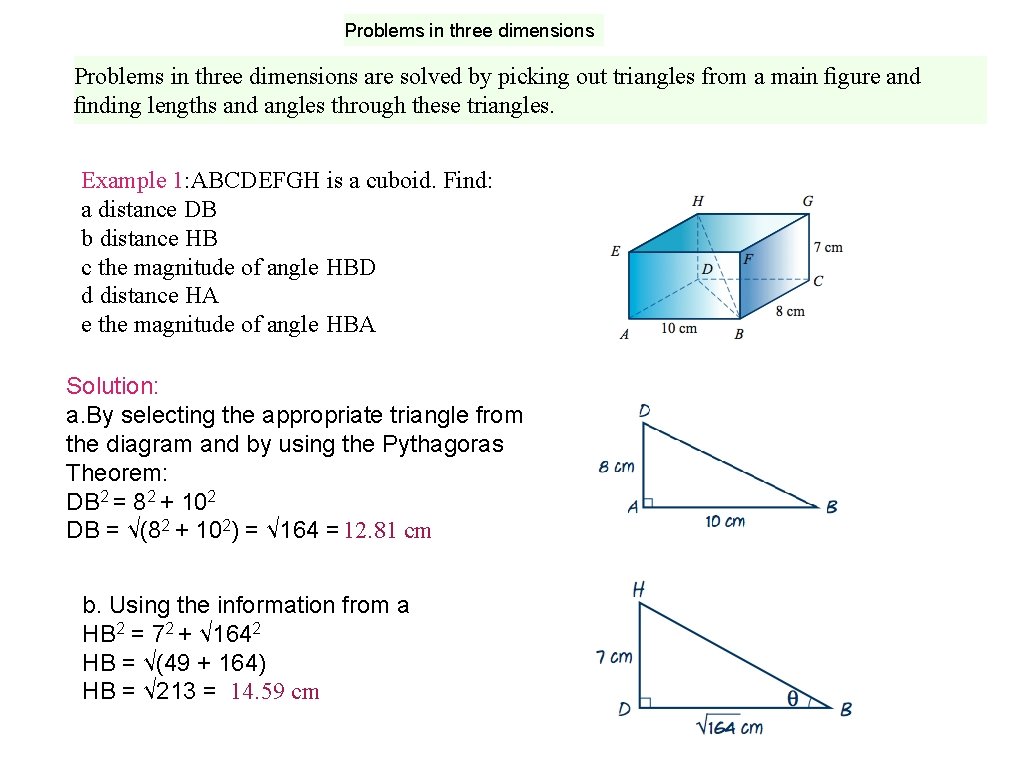
Problems in three dimensions are solved by picking out triangles from a main figure and finding lengths and angles through these triangles. Example 1: ABCDEFGH is a cuboid. Find: a distance DB b distance HB c the magnitude of angle HBD d distance HA e the magnitude of angle HBA Solution: a. By selecting the appropriate triangle from the diagram and by using the Pythagoras Theorem: DB 2 = 82 + 102 DB = √(82 + 102) = √ 164 = 12. 81 cm b. Using the information from a HB 2 = 72 + √ 1642 HB = √(49 + 164) HB = √ 213 = 14. 59 cm

c. tanθ = 7 √ 164 θ = tan-1 7 √ 164 θ = 28. 66◦ d. Use the triangle HAD HA 2 = 82 + 72 HA = √(82 + 72 ) = √ 113 cm e. 3 sides-cosine rule cos. B = 102 +√ 2132 -√ 1132 2× 10×√ 213 cos. B =0. 68518 B =46. 75◦

Example 2: The diagram shows a pyramid with a square base. The base has sides 6 cm long and the edges VA, VB, VC, VD are each 10 cm long. a Find the length of DB. b Find the length of BE. c Find the length of VE. d Find the magnitude of angle VBE. Give all answers correct to two decimal places. Solution: a DB 2 = 62 + 62 DB = √( 62 + 62 ) DB = 8. 49 cm b BE = 8. 49/2 = 4. 24 cm c VE = √( 102 - 4. 242) = 9. 06 cm d sin (VBE) = 9. 06 10 VBE = sin-1(9. 06/10) = 64. 90°

Example 3: A communications mast is erected at the corner A of a rectangular courtyard ABCD whose sides measure 60 m and 45 m. If the angle of elevation of the top of the mast from C is 12◦ , find: a the height of the mast b the angle of elevation of the top of the mast from B (where AB = 45 m) Give answers cor rect to two decimal places. Solution : a We need to find AC first. AC = √(452 + 602) = 75 m Then we can use AC to find the height of the mast. tan(12°) = HA 75 HA = 75 tan (12°) = 15. 94 m b tanθ = 15. 94 45 θ = tan-1( 15. 94/45) = 19. 51◦

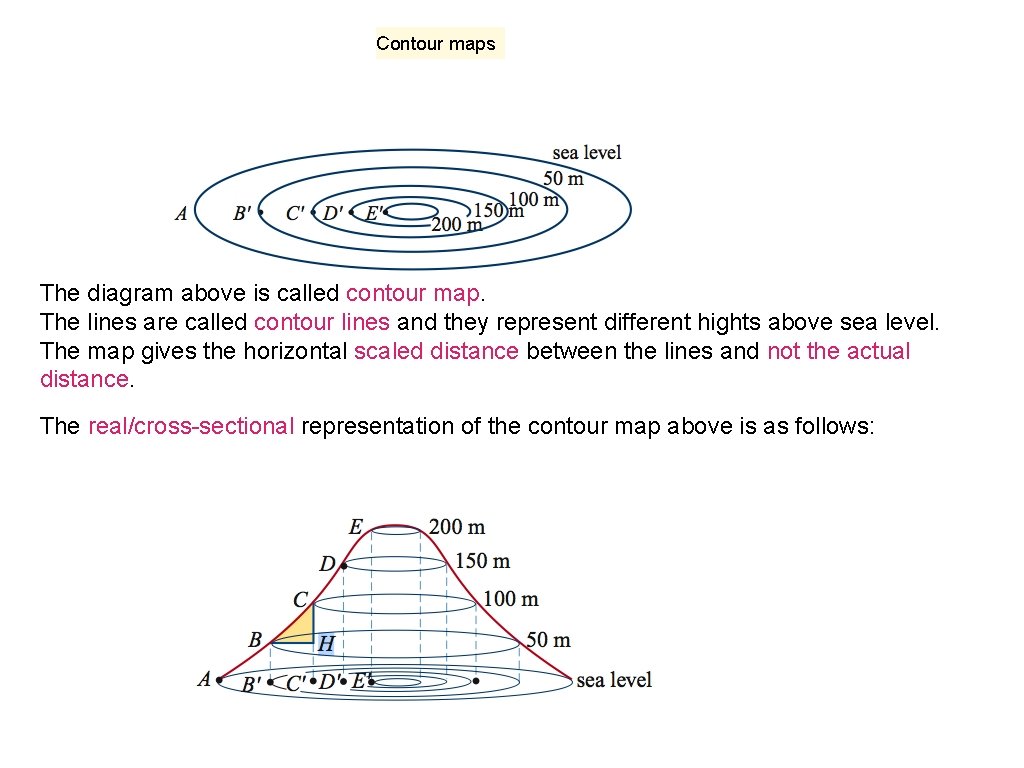
Contour maps The diagram above is called contour map. The lines are called contour lines and they represent different hights above sea level. The map gives the horizontal scaled distance between the lines and not the actual distance. The real/cross-sectional representation of the contour map above is as follows:

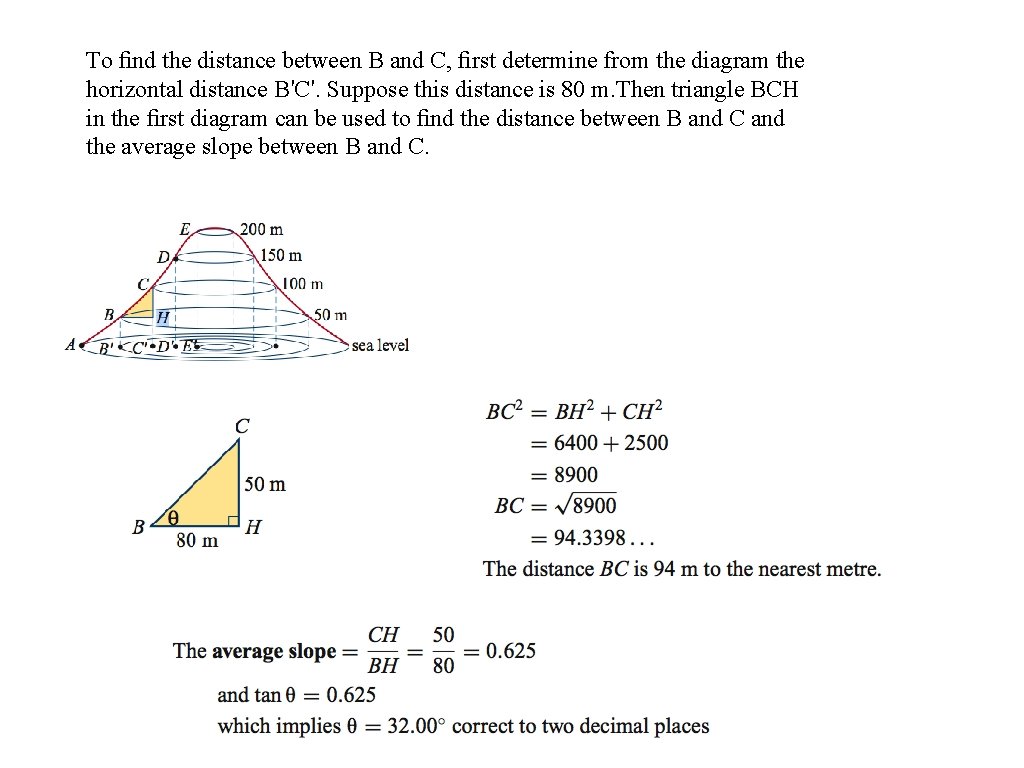
To find the distance between B and C, first determine from the diagram the horizontal distance B′C′. Suppose this distance is 80 m. Then triangle BCH in the first diagram can be used to find the distance between B and C and the average slope between B and C.

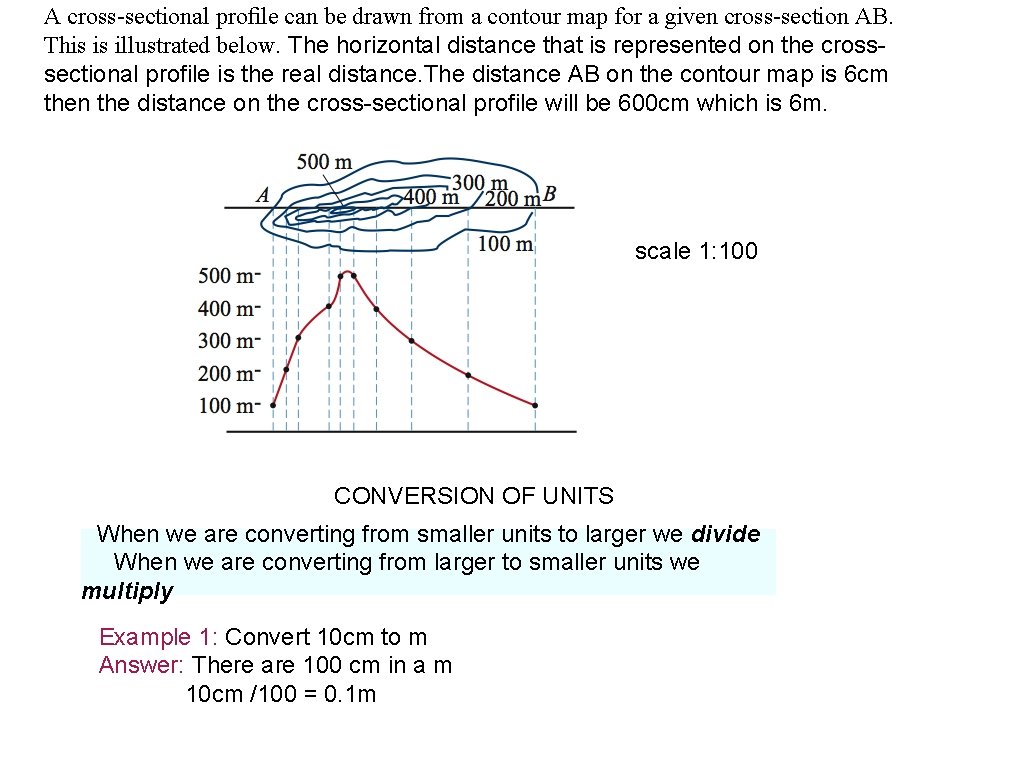
A cross-sectional profile can be drawn from a contour map for a given cross-section AB. This is illustrated below. The horizontal distance that is represented on the crosssectional profile is the real distance. The distance AB on the contour map is 6 cm then the distance on the cross-sectional profile will be 600 cm which is 6 m. scale 1: 100 CONVERSION OF UNITS When we are converting from smaller units to larger we divide When we are converting from larger to smaller units we multiply Example 1: Convert 10 cm to m Answer: There are 100 cm in a m 10 cm /100 = 0. 1 m

Conversion of units of length a 1 cm (mm) = 1 × 10 = 10 mm b 1 m (cm) = 1 × 100 = 100 cm c 1 km (m) = 1 × 1000 = 1000 km d 1 mm(cm) = 1/10 = 0. 1 cm e 1 cm ( m) = 1/100 = 0. 01 m f 1 m (km) = 1/1000 = 0. 001 km Conversion of units of area 1 cm 2 (mm 2) = 1 × 102 = 100 mm 2 1 m 2 (cm 2) = 1 × 1002 = 10000 cm 2 = 104 cm 2 1 km 2 (m 2) = 1 × 10002 = 1000000 km 2 = 106 km 2 1 mm 2(cm 2) = 1/102 = 0. 01 cm 2 = 10 -2 cm 2 1 cm 2 (m 2) = 1/1002 = 0. 0001 m 2 = 10 -4 m 2 1 m 2 (km 2) = 1/10002 = 0. 000001 km 2= 10 -6 Example: a Convert 156000 m 2 to km 2 Answer: 156000 m 2 / 10002 = 156000/1000000 = 0. 156 km 2 b Convert 20000 mm 2 to cm 2 Answer: 20000 mm 2 /102 = 20000/100 = 200 cm 2

Conversion of units of volume 1000 mm 3 (cm 3) = 1000/103 = 1000/1000 = 1 cm 3 1000000 cm 3(m 3) = 1000000/1003 = 1000000/1000000 = 1 m 3 1 litre = 1000 cm 3 1000 litres = 1 m 3