7 2 Parallel and Perpendicular Lines Warm Up

















- Slides: 21

7 -2 Parallel and Perpendicular Lines Warm Up Complete each sentence. 1. Angles whose measures have a sum of 90° are ________. complementary 2. Vertical angles have equal measures, so they are congruent _______. 3. Angles whose measures have a sum of 180° are supplementary _______. 4. A part of a line between two points is called a segment ______. Course 3

7 -2 Parallel and Perpendicular Lines Problem of the Day The square root of 1, 813, 141, 561 is a whole number. Is it odd or even? How do you know? Odd: An odd number can only be the product of two odd numbers. Course 3

7 -2 Parallel and Perpendicular Lines Learn to identify parallel and perpendicular lines and the angles formed by a transversal. Course 3

Parallel. Lesson and Perpendicular 7 -2 Insert Title Here. Lines Vocabulary parallel lines perpendicular lines transversal Course 3

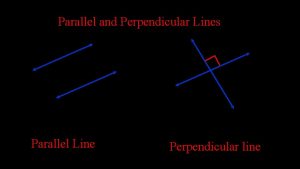
7 -2 Parallel and Perpendicular Lines Parallel lines are lines in a plane that never meet, like a set of perfectly straight, infinite train tracks. Perpendicular lines are lines that intersect at 90° angles. Course 3

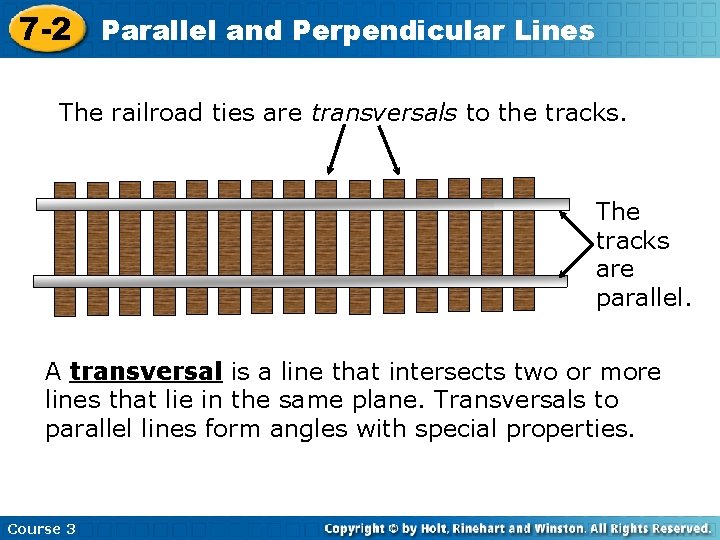
7 -2 Parallel and Perpendicular Lines The railroad ties are transversals to the tracks. The tracks are parallel. A transversal is a line that intersects two or more lines that lie in the same plane. Transversals to parallel lines form angles with special properties. Course 3

7 -2 Parallel and Perpendicular Lines Caution! You cannot tell for certain if angles are congruent by measuring because measurement is not exact. Course 3

7 -2 Parallel and Perpendicular Lines Additional Example 1: Identifying Congruent Angles Formed by a Transversal Measure the angles formed by the transversal and parallel lines. Which angles seem to be congruent? 1, 3, 5, and 7 all measure 150°. 2, 4, 6, and 8 all measure 30°. Course 3

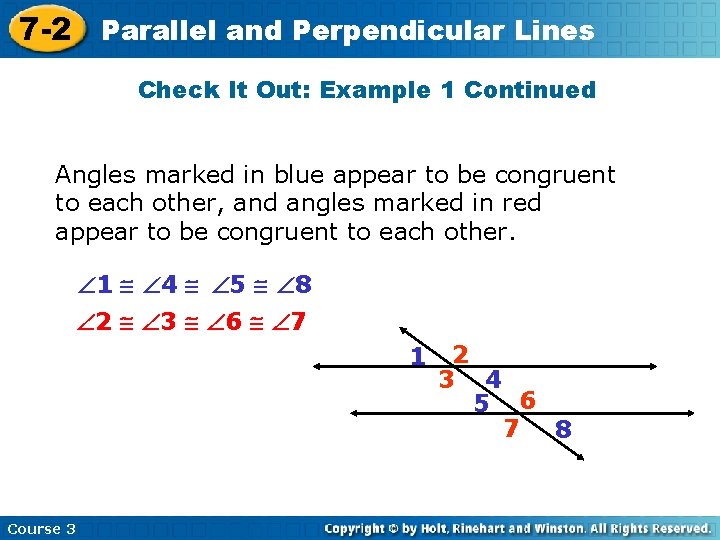
7 -2 Parallel and Perpendicular Lines Additional Example 1 Continued Angles marked in blue appear to be congruent to each other, and angles marked in red appear to be congruent to each other. 1 @ 3 @ 5 @ 7 2 @ 4 @ 6 @ 8 Course 3 2 1 3 4 6 5 7 8

7 -2 Parallel and Perpendicular Lines Check It Out: Example 1 Measure the angles formed by the transversal and parallel lines. Which angles seem to be congruent? 1 2 3 4 5 6 7 8 1, 4, 5, and 8 all measure 36°. 2, 3, 6, and 7 all measure 144°. Course 3

7 -2 Parallel and Perpendicular Lines Check It Out: Example 1 Continued Angles marked in blue appear to be congruent to each other, and angles marked in red appear to be congruent to each other. 1 @ 4 @ 5 @ 8 2 @ 3 @ 6 @ 7 1 Course 3 2 3 4 5 6 7 8

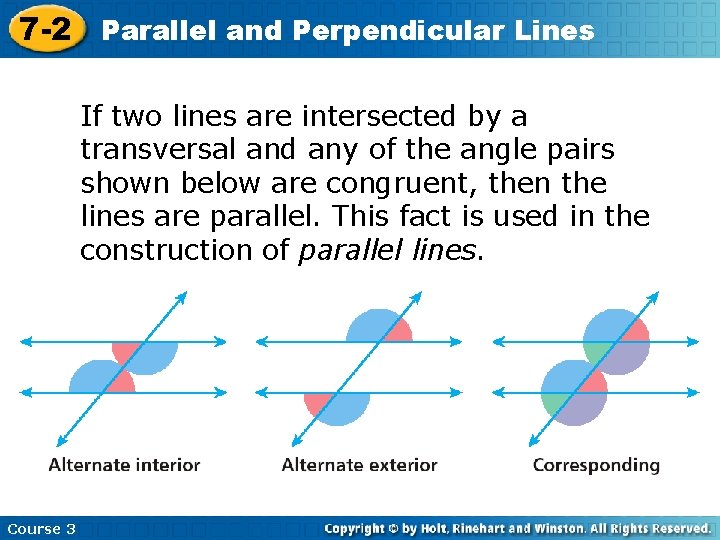
7 -2 Parallel and Perpendicular Lines If two lines are intersected by a transversal and any of the angle pairs shown below are congruent, then the lines are parallel. This fact is used in the construction of parallel lines. Course 3

7 -2 Parallel and Perpendicular Lines PROPERTIES OF TRANSVERSALS TO PARALLEL LINES If two parallel lines are intersected by a transversal, • the acute angles that are formed are all congruent, • the obtuse angles are all congruent, • and any acute angle is supplementary to any obtuse angle. If the transversal is perpendicular to the parallel lines, all of the angles formed are congruent 90° angles. Course 3

7 -2 Parallel and Perpendicular Lines Writing Math The symbol for parallel is ||. The symbol for perpendicular is . Course 3

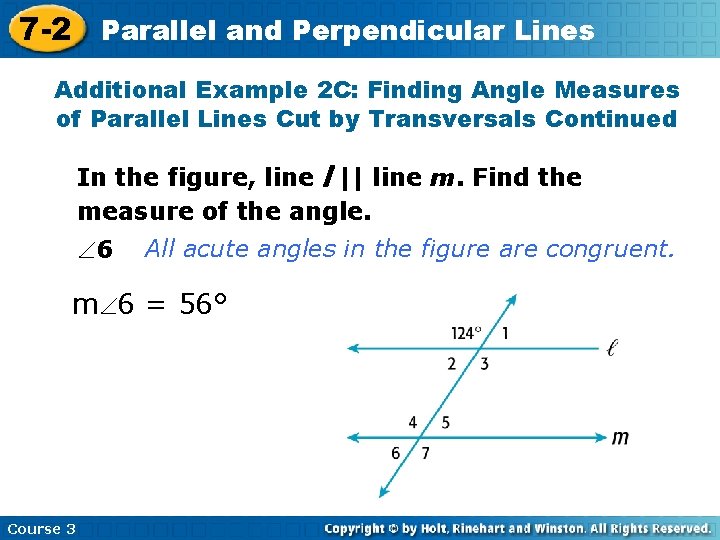
7 -2 Parallel and Perpendicular Lines Additional Example 2 A: Finding Angle Measures of Parallel Lines Cut by Transversals In the figure, line l || line m. Find the measure of the angle. 4 All obtuse angles in the figure are congruent. m 4 = 124° Course 3

7 -2 Parallel and Perpendicular Lines Additional Example 2 B: Finding Angle Measures of Parallel Lines Cut by Transversals Continued In the figure, line l || line m. Find the measure of the angle. 2 2 is supplementary to the angle 124°. m 2 + 124° = 180° – 124° m 2 = 56° Course 3

7 -2 Parallel and Perpendicular Lines Additional Example 2 C: Finding Angle Measures of Parallel Lines Cut by Transversals Continued In the figure, line l || line m. Find the measure of the angle. 6 All acute angles in the figure are congruent. m 6 = 56° Course 3

7 -2 Parallel and Perpendicular Lines Check It Out: Example 2 A In the figure, line n || line m. Find the measure of the angle. 7 All obtuse angles in the figure are congruent m 7 = 144° Course 3 1 144° 3 4 5 6 7 8 m n

7 -2 Parallel and Perpendicular Lines Check It Out: Example 2 B In the figure, line n || line m. Find the measure of the angle. 5 5 is supplementary to the angle 144°. m 5 + 144° = 180° – 144° m 5 = 36° Course 3 1 144° 3 4 5 6 7 8 m n

7 -2 Parallel and Perpendicular Lines Check It Out: Example 2 C In the figure, line n || line m. Find the measure of the angle. 1 All acute angles in the figure are congruent m 1 = 36° Course 3 1 144° 3 4 5 6 7 8 m n

7 -2 Parallel and Perpendicular Lines Lesson Quiz In the figure a || b. 1. Name the angles congruent to 3. 1, 5, 7 2. Name all the angles supplementary to 6. 1, 3, 5, 7 3. If m 1 = 105° what is m 3? 105° 4. If m 5 = 120° what is m 2? 60° Course 3
 Unit 3 test parallel and perpendicular lines answer key
Unit 3 test parallel and perpendicular lines answer key Parallel lines
Parallel lines Parallel lines slope
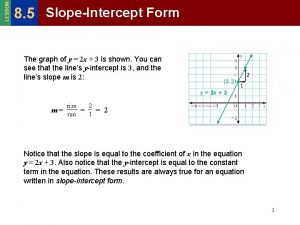
Parallel lines slope Parallel and perpendicular slopes
Parallel and perpendicular slopes Parallel and perpendicular lines
Parallel and perpendicular lines Slopes of parallel and perpendicular lines assignment
Slopes of parallel and perpendicular lines assignment Lesson 8 parallel and perpendicular lines
Lesson 8 parallel and perpendicular lines Geometry chapter 3 review parallel and perpendicular lines
Geometry chapter 3 review parallel and perpendicular lines Perpendicular line in real life
Perpendicular line in real life Chapter 3 review parallel and perpendicular lines
Chapter 3 review parallel and perpendicular lines Chapter 3 parallel and perpendicular lines
Chapter 3 parallel and perpendicular lines Chapter 3 quiz geometry answers
Chapter 3 quiz geometry answers Lesson 2-4 parallel and perpendicular lines
Lesson 2-4 parallel and perpendicular lines E.6 equations of parallel and perpendicular lines
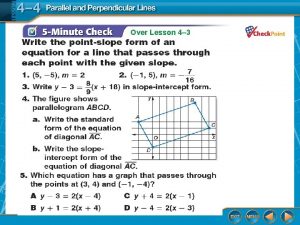
E.6 equations of parallel and perpendicular lines 4-4 parallel and perpendicular lines
4-4 parallel and perpendicular lines Materacademyfl
Materacademyfl 3 sets of parallel lines
3 sets of parallel lines Slopes of parallel and perpendicular lines lesson 8-1
Slopes of parallel and perpendicular lines lesson 8-1 Properties of perpendicular lines
Properties of perpendicular lines 3-8 slopes of parallel and perpendicular lines
3-8 slopes of parallel and perpendicular lines 5-6 parallel and perpendicular lines
5-6 parallel and perpendicular lines 5-6 parallel and perpendicular lines
5-6 parallel and perpendicular lines