LESSON 8 5 SlopeIntercept Form The graph of

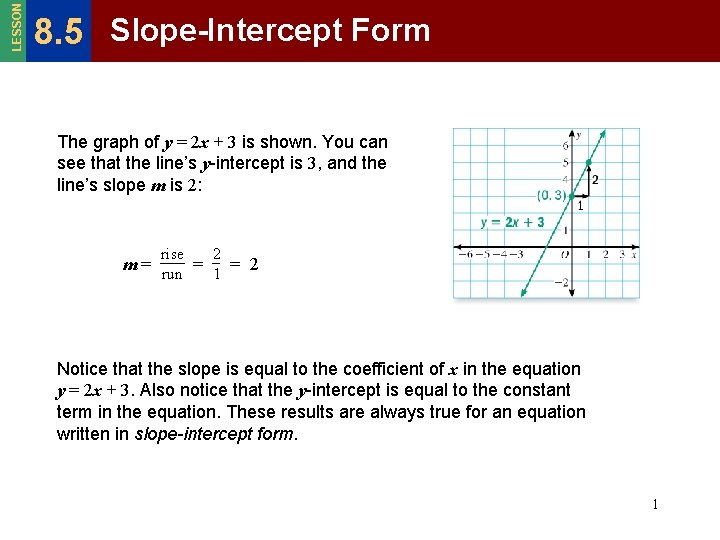
LESSON 8. 5 Slope-Intercept Form The graph of y = 2 x + 3 is shown. You can see that the line’s y-intercept is 3, and the line’s slope m is 2: rise 2 m = run = 1 = 2 Notice that the slope is equal to the coefficient of x in the equation y = 2 x + 3. Also notice that the y-intercept is equal to the constant term in the equation. These results are always true for an equation written in slope-intercept form. 1

LESSON 8. 5 Slope-Intercept Form Words A linear equation of the form y = mx + b is said to be in slope-intercept form. The slope is m and the y-intercept is b. Algebra y = mx + b Numbers y = 2 x + 3 2

LESSON 8. 5 Slope-Intercept Form EXAMPLE 1 Identifying the Slope and y-Intercept Identify the slope and y-intercept of the line with the given equation. 3 x + 5 y = 10 SOLUTION Write the equation 3 x + 5 y = 10 in slope-intercept form by solving for y. 3 x + 5 y = 10 Write original equation. 5 y = – 3 x + 10 3 y = – 5 x + 2 ANSWER Subtract 3 x from each side. Multiply each side by 1. 5 The line has a slope of – 3 and a y-intercept of 2. 5 3

LESSON 8. 5 Slope-Intercept Form EXAMPLE 2 Graphing an Equation in Slope-Intercept Form Graph the equation y = – 2 x + 4. 3 1 The y-intercept is 4, so plot the point (0, 4). 2 The slope is – 2 = – 2. 3 3 Starting at (0, 4), plot another point by moving right 3 units and down 2 units. 3 Draw a line through the two points. 4

LESSON 8. 5 Slope-Intercept Form Real-Life Situations In a real-life problem involving a linear equation, the y-intercept is often an initial value, and the slope is a rate of change. 5

LESSON 8. 5 Slope-Intercept Form EXAMPLE 3 Using Slope and y-intercept in Real Life Earth Science The temperature at Earth’s surface averages about 20˚C. In the crust below the surface, the temperature rises by about 25˚C per kilometer of depth. Write an equation that approximates the temperature below Earth’s surface as a function of depth. SOLUTION Let x be the depth (in kilometers) below Earth’s surface, and let y be the temperature (in degrees Celsius) at that depth. Write a verbal model. Then use the verbal model to write an equation. Temperature Rate of change Depth = + • below surface at surface In temperature below surface y = 20 + 25 x 6

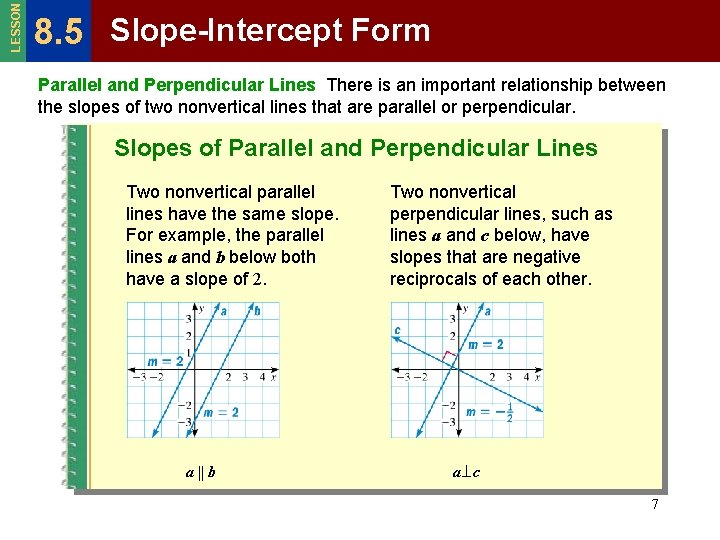
LESSON 8. 5 Slope-Intercept Form Parallel and Perpendicular Lines There is an important relationship between the slopes of two nonvertical lines that are parallel or perpendicular. Slopes of Parallel and Perpendicular Lines Two nonvertical parallel lines have the same slope. For example, the parallel lines a and b below both have a slope of 2. a || b Two nonvertical perpendicular lines, such as lines a and c below, have slopes that are negative reciprocals of each other. a c 7

LESSON 8. 5 Slope-Intercept Form EXAMPLE 4 Finding Slopes of Parallel and Perpendicular Lines Find the slopes of the lines that are parallel and perpendicular to the line with equation 4 x + 3 y = – 18. SOLUTION First write the given equation in slope-intercept form. 4 x + 3 y = – 18 Write original equation. 3 y = – 4 x – 18 y = – 4 x – 6 3 Subtract 4 x from each side. 1 Multiply each side by 3. The slope of the given line is – 4. Because parallel lines have the same slope, 3 the slope of a parallel line is also – 4. The slope of a perpendicular line is the 3 4 3 negative reciprocal of – , or. 3 4 8