5 8 Slopes of Parallel and Perpendicular Lines

5 -8 Slopes of Parallel and Perpendicular Lines Objectives Identify and graph parallel and perpendicular lines. Write equations to describe lines parallel or perpendicular to a given line. Holt Algebra 1

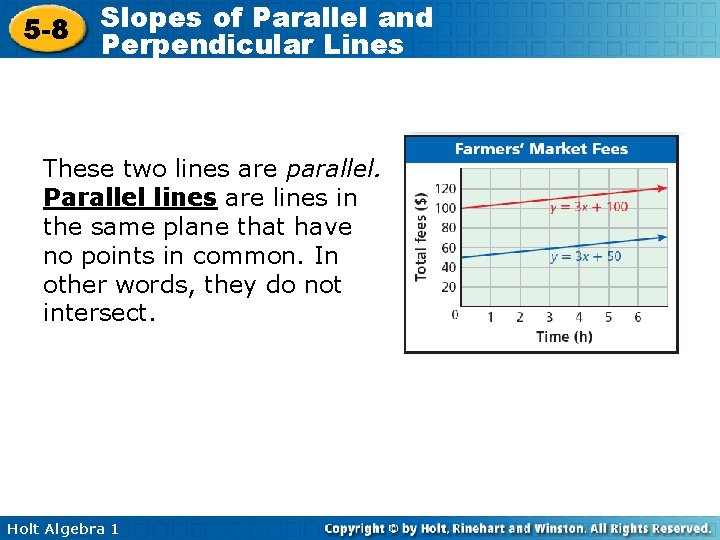
5 -8 Slopes of Parallel and Perpendicular Lines These two lines are parallel. Parallel lines are lines in the same plane that have no points in common. In other words, they do not intersect. Holt Algebra 1

5 -8 Slopes of Parallel and Perpendicular Lines Holt Algebra 1

5 -8 Slopes of Parallel and Perpendicular Lines Identify which pairs of lines are parallel. (Must have the exact same slope) 1. y = ⅔ x + 5 and y = -⅔ x + 1 2. y = -6 x + 4 and y = -6 x - 3 3. y = ⅘ x – 2 and y = ⅘ x + 6 Write an equation parallel to y = 2 x – 1 (Must have the exact same slope as this equation) Holt Algebra 1

5 -8 Slopes of Parallel and Perpendicular Lines Example 1 B Continued Identify which lines are parallel. y = 2 x – 3 y = -⅔ x + 3 2 x + 3 y = 8 y + 1 = 3(x – 3) Make sure all equations are in slope-intercept form to determine the slope. 2 x + 3 y = 8 y + 1 = 3(x – 3) – 2 x y + 1 = 3 x – 9 3 y = – 2 x + 8 – 1 y = 3 x – 10 Holt Algebra 1

5 -8 Slopes of Parallel and Perpendicular Lines Example 1 B Continued Graph all four equations The lines described by y = 2 x – 3 and y + 1 = 3(x – 3) are not parallel with any of the lines. The lines described by y = 2 x – 3 and represent parallel lines. They each have the slope Holt Algebra 1 . y + 1 = 3(x – 3)

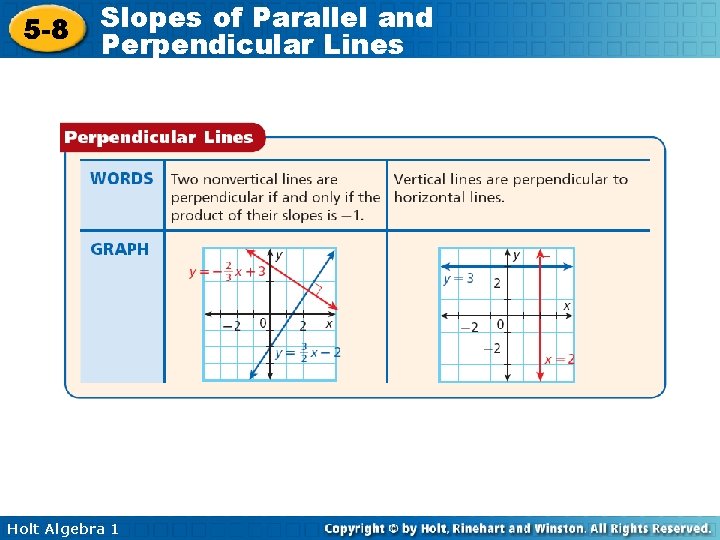
5 -8 Slopes of Parallel and Perpendicular Lines Perpendicular lines are lines that intersect to form right angles (90°). Perpendicular lines have opposite reciprocal slopes. 1. Flip the fraction 2. Change the sign Example: -3/5 and 5/3 Holt Algebra 1 Example: 2/1 and -1/2

5 -8 Slopes of Parallel and Perpendicular Lines Holt Algebra 1

5 -8 Slopes of Parallel and Perpendicular Lines Identify which pairs of lines are perpendicular. (Must have opposite reciprocal slopes) 1. y = ⅔ x + 5 and y = -⅔ x + 6 2. y = -6 x + 4 and y = ⅙ x + 1 3. y = -x – 2 and y = x - 3 Write an equation perpendicular to y = -¾x + 1 (Must have an opposite reciprocal slope to this one) Holt Algebra 1

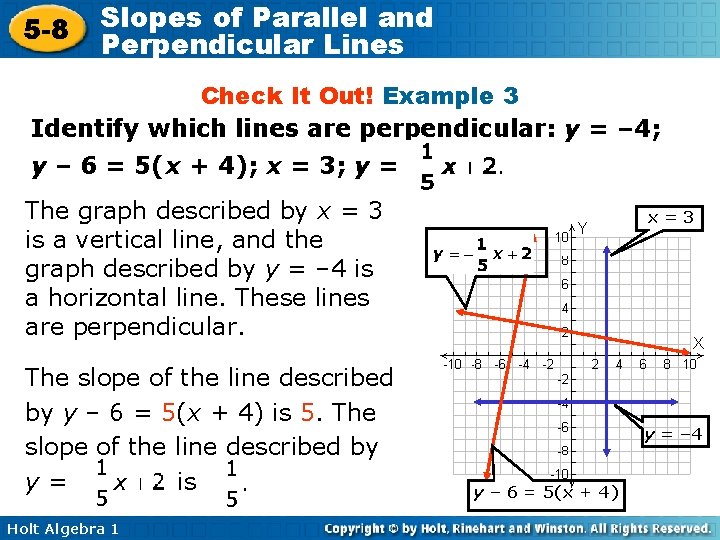
5 -8 Slopes of Parallel and Perpendicular Lines Check It Out! Example 3 Identify which lines are perpendicular: y = – 4; y – 6 = 5(x + 4); x = 3; y = The graph described by x = 3 is a vertical line, and the graph described by y = – 4 is a horizontal line. These lines are perpendicular. The slope of the line described by y – 6 = 5(x + 4) is 5. The slope of the line described by y= is Holt Algebra 1 x=3 y = – 4 y – 6 = 5(x + 4)

5 -8 Slopes of Parallel and Perpendicular Lines Example 5 A: Writing Equations of Parallel and Perpendicular Lines Write an equation in slope-intercept form for the line that passes through (4, 10) and is parallel to the line described by y = 3 x + 8. Step 1 Find the slope of the line. The slope is 3. y = 3 x + 8 The parallel line also has a slope of 3. Step 2 Write the equation in point-slope form. y – y 1 = m(x – x 1) Use the point-slope form. y – 10 = 3(x – 4) Substitute 3 for m, 4 for x 1, and 10 for y 1. Holt Algebra 1

5 -8 Slopes of Parallel and Perpendicular Lines Example 5 A Continued Write an equation in slope-intercept form for the line that passes through (4, 10) and is parallel to the line described by y = 3 x + 8. Step 3 Write the equation in slope-intercept form. y – 10 = 3(x – 4) y – 10 = 3 x – 12 y = 3 x – 2 Holt Algebra 1 Distribute 3 on the right side. Add 10 to both sides.

5 -8 Slopes of Parallel and Perpendicular Lines Example 5 B: Writing Equations of Parallel and Perpendicular Lines Write an equation in slope-intercept form for the line that passes through (2, – 1) and is perpendicular to the line described by y = 2 x – 5. Step 1 Find the slope of the line. The slope is 2. y = 2 x – 5 The perpendicular line has a slope of because Step 2 Write the equation in point-slope form. Use the point-slope form. y – y 1 = m(x – x 1) Holt Algebra 1 Substitute and 2 for x 1. for m, – 1 for y 1,

5 -8 Slopes of Parallel and Perpendicular Lines Example 5 B Continued Write an equation in slope-intercept form for the line that passes through (2, – 1) and is perpendicular to the line described by y = 2 x – 5. Step 3 Write the equation in slope-intercept form. Distribute on the right side. Subtract 1 from both sides. Holt Algebra 1

5 -8 Slopes of Parallel and Perpendicular Lines 1. Determine if the two equations are perpendicular Hint: make sure each looks like y = mx + b first 2 y – 8 = 3 x and y = ⅔ x + 1 2. Write an equation for the line that goes through the point (2, 1) and is parallel to y = -3 x + 2. Hint: Plug m, x, and y into (y – y 1)=m(x – x 1) Holt Algebra 1