5 2 Proving That Lines Are Parallel Objective

5. 2 Proving That Lines Are Parallel Objective: After studying this section, you will be able to apply the exterior angle inequality theorem and use various methods to prove lines are parallel.

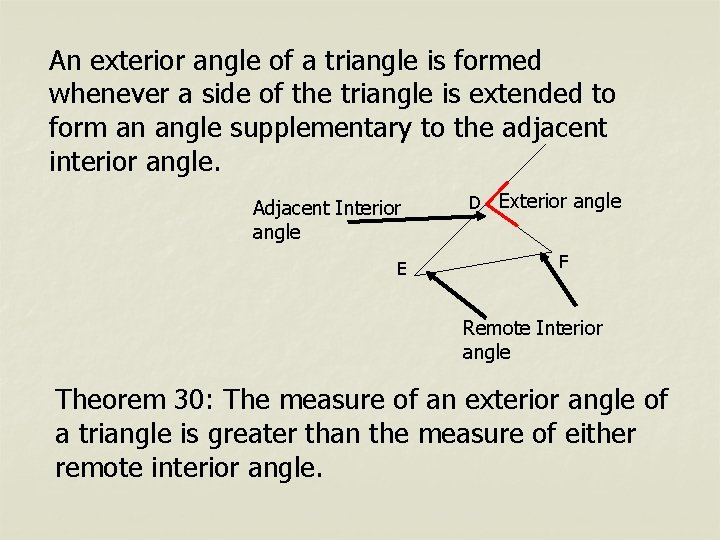
An exterior angle of a triangle is formed whenever a side of the triangle is extended to form an angle supplementary to the adjacent interior angle. Adjacent Interior angle E D Exterior angle F Remote Interior angle Theorem 30: The measure of an exterior angle of a triangle is greater than the measure of either remote interior angle.

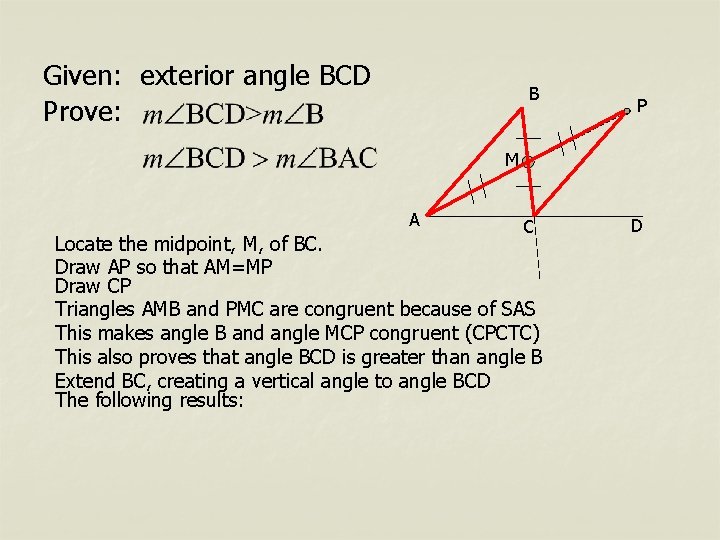
Given: exterior angle BCD Prove: B P M A C Locate the midpoint, M, of BC. Draw AP so that AM=MP Draw CP Triangles AMB and PMC are congruent because of SAS This makes angle B and angle MCP congruent (CPCTC) This also proves that angle BCD is greater than angle B Extend BC, creating a vertical angle to angle BCD The following results: D

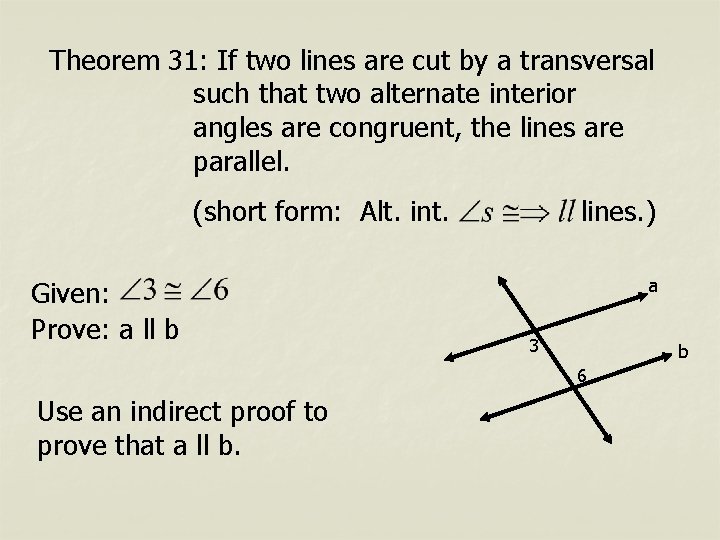
Theorem 31: If two lines are cut by a transversal such that two alternate interior angles are congruent, the lines are parallel. (short form: Alt. int. Given: Prove: a ll b lines. ) a 3 b 6 Use an indirect proof to prove that a ll b.

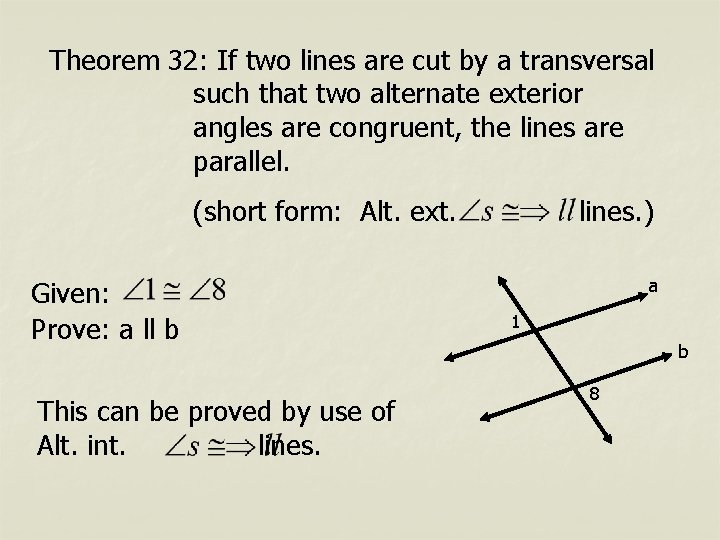
Theorem 32: If two lines are cut by a transversal such that two alternate exterior angles are congruent, the lines are parallel. (short form: Alt. ext. Given: Prove: a ll b This can be proved by use of Alt. int. lines. ) a 1 b 8

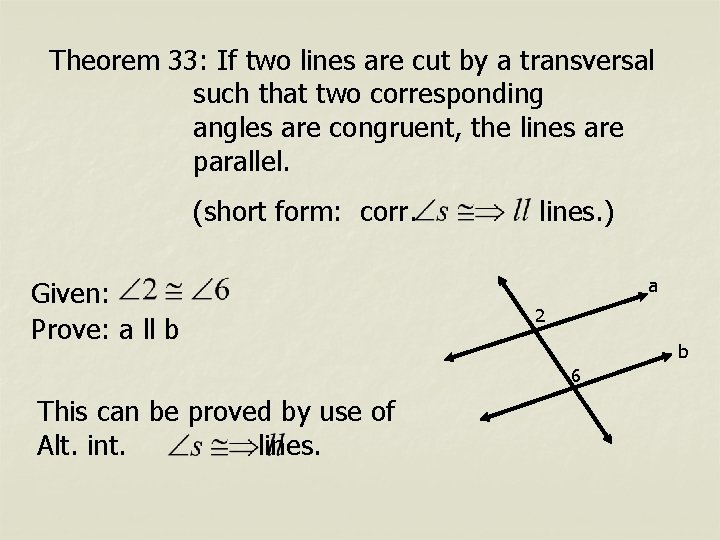
Theorem 33: If two lines are cut by a transversal such that two corresponding angles are congruent, the lines are parallel. (short form: corr. Given: Prove: a ll b lines. ) a 2 b 6 This can be proved by use of Alt. int. lines.

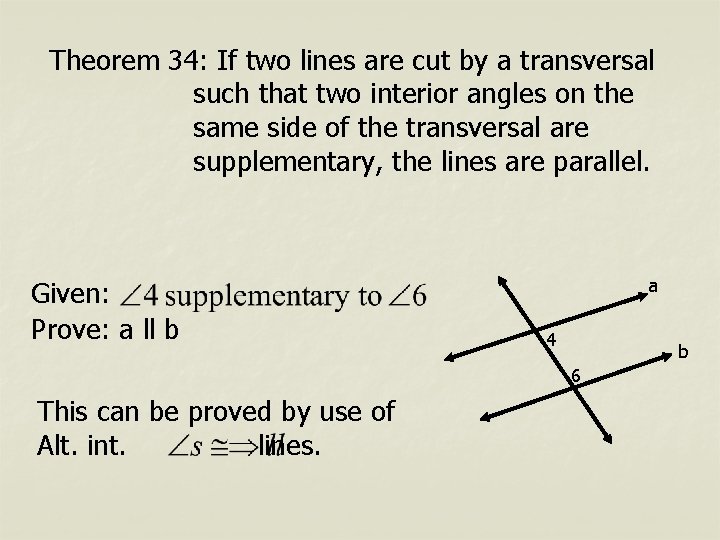
Theorem 34: If two lines are cut by a transversal such that two interior angles on the same side of the transversal are supplementary, the lines are parallel. Given: Prove: a ll b a 4 b 6 This can be proved by use of Alt. int. lines.

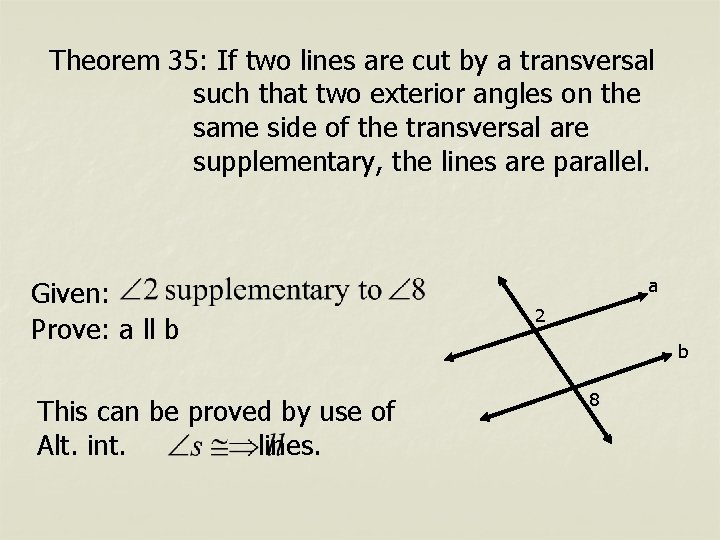
Theorem 35: If two lines are cut by a transversal such that two exterior angles on the same side of the transversal are supplementary, the lines are parallel. Given: Prove: a ll b This can be proved by use of Alt. int. lines. a 2 b 8

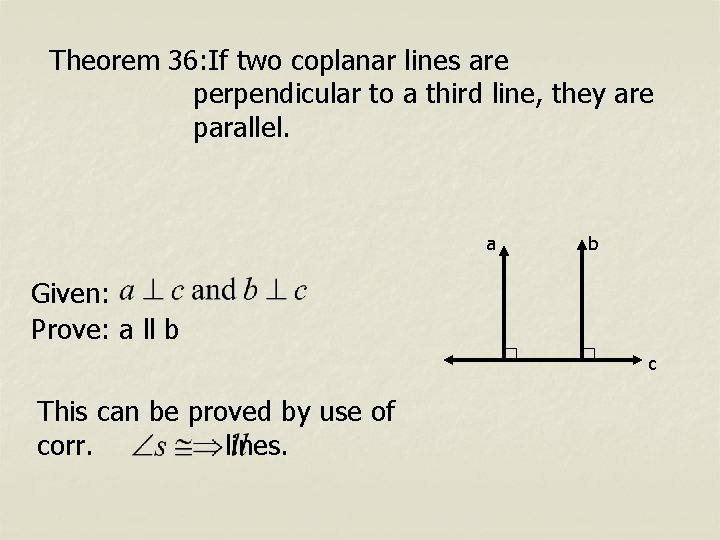
Theorem 36: If two coplanar lines are perpendicular to a third line, they are parallel. a b Given: Prove: a ll b c This can be proved by use of corr. lines.

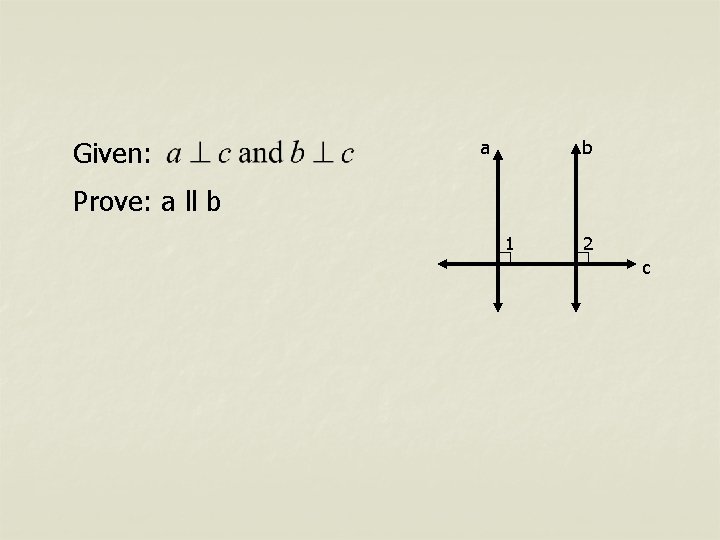
Given: a b Prove: a ll b 1 2 c

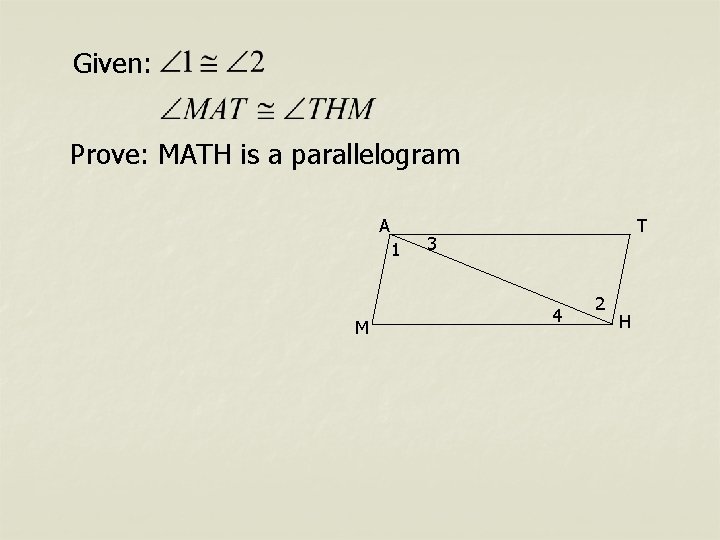
Given: Prove: MATH is a parallelogram A 1 M T 3 4 2 H

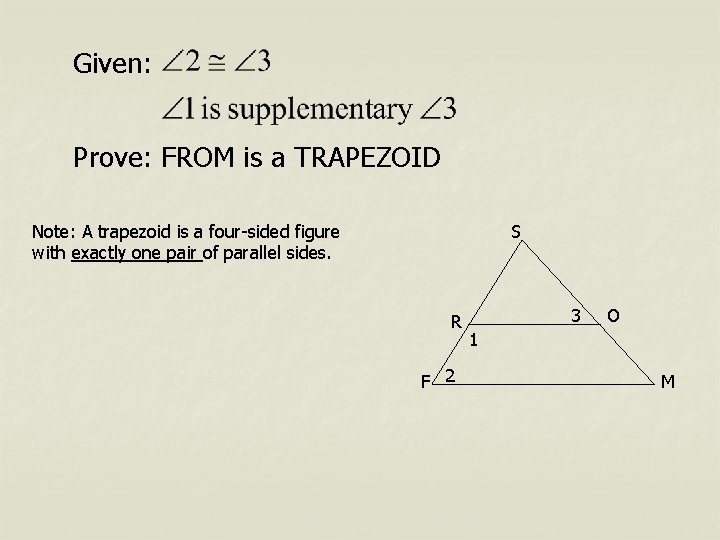
Given: Prove: FROM is a TRAPEZOID Note: A trapezoid is a four-sided figure with exactly one pair of parallel sides. S R F 2 3 O 1 M

Summary Name the different ways to prove lines are parallel. Homework: worksheet