Introduction The slopes of parallel lines are always
- Slides: 33
Introduction The slopes of parallel lines are always equal, whereas the slopes of perpendicular lines are always opposite reciprocals. It is important to be able to determine whether lines are parallel or perpendicular, but the creation of parallel and perpendicular lines is also important. In this lesson, you will write the equations of lines that are parallel and perpendicular to a given line through a given point. 1 6. 1. 2: Working with Parallel and Perpendicular Lines
Key Concepts • You can write the equation of a line through a given point that is parallel to a given line if you know the equation of the given line. It is necessary to identify the slope of the given equation before trying to write the equation of the line that is parallel or perpendicular. • Writing the given equation in slope-intercept form allows you to quickly identify the slope, m, of the equation. 2 6. 1. 2: Working with Parallel and Perpendicular Lines
Key Concepts, continued • If the given equation is not in slope-intercept form, take a few moments to rewrite it. Writing Equations Parallel to a Given Line Through a Given Point 1. Rewrite the given equation in slope-intercept form if necessary. 2. Identify the slope of the given line. 3. Write the general point-slope form of a linear equation: y – y 1 = m(x – x 1). 4. Substitute the slope of the given line for m in the general equation. 5. Substitute x and y from the given point into the general equation for x 1 and y 1. 6. Simplify the equation. 7. Rewrite the equation in slope-intercept form if necessary. 6. 1. 2: Working with Parallel and Perpendicular Lines 3
Key Concepts, continued • Writing the equation of a line perpendicular to a given line through a given point is similar to writing equations of parallel lines. • The slopes of perpendicular lines are opposite reciprocals. 4 6. 1. 2: Working with Parallel and Perpendicular Lines
Key Concepts, continued Writing Equations Perpendicular to a Given Line Through a Given Point 1. 2. 3. 4. 5. 6. 7. 8. Rewrite the given equation in slope-intercept form if necessary. Identify the slope of the given line. Find the opposite reciprocal of the slope of the given line. Write the general point-slope form of a linear equation: y – y 1 = m(x – x 1). Substitute the opposite reciprocal of the given line for m in the general equation. Substitute x and y from the given point into the general equation for x 1 and y 1. Simplify the equation. Rewrite the equation in slope-intercept form if necessary. 5 6. 1. 2: Working with Parallel and Perpendicular Lines
Key Concepts, continued • The shortest distance between two points is a line. • The shortest distance between a given point and a given line is the line segment that is perpendicular to the given line through the given point. 6 6. 1. 2: Working with Parallel and Perpendicular Lines
Key Concepts, continued Writing Equations Perpendicular to a Given Line Through a Given Point 1. Follow the steps outlined previously to find the equation of the line that is perpendicular to the given line through the given point. 2. Find the intersection between the two lines by setting the given equation and the equation of the perpendicular line equal to each other. 3. Solve for x. 4. Substitute the x-value into the equation of the given line to find the y-value. 5. Find the distance between the given point and the point of intersection of the given line and the perpendicular line using the distance formula, . 6. 1. 2: Working with Parallel and Perpendicular Lines 7
Common Errors/Misconceptions • attempting to identify the slope of the given line without transforming the equation into slope-intercept form • incorrectly identifying the slope of the given line • incorrectly finding the slope of the line parallel to the given line • incorrectly identifying the slope of the line perpendicular to the given line • improperly substituting the x- and y-values into the general point-slope equation 8 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice Example 1 Write the slope-intercept form of an equation for the line that passes through the point (5, – 2) and is parallel to the graph of 8 x – 2 y = 6. 9 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 1, continued 1. Rewrite the given equation in slopeintercept form. 8 x – 2 y = 6 – 8 x y = – 3 + 4 x y = 4 x – 3 Given equation Subtract 8 x from both sides. Divide both sides by – 2. Write the equation in slopeintercept form. 10 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 1, continued 2. Identify the slope of the given line. The slope of the line y = 4 x – 3 is 4. 11 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 1, continued 3. Substitute the slope of the given line for m in the point-slope form of a linear equation. y – y 1 = m(x – x 1) y – y 1 = 4(x – x 1) Point-slope form Substitute m from the given equation. 12 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 1, continued 4. Substitute x and y from the given point into the equation for x 1 and y 1. y – y 1 = 4(x – x 1) y – (– 2) = 4(x – 5) y 1. Equation Substitute (5, – 2) for x 1 and 13 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 1, continued 5. Simplify the equation. y – (– 2) = 4(x – 5) y – (– 2) = 4 x – 20 y + 2 = 4 x – 20 y = 4 x – 22 Equation with substituted values for x 1 and y 1 Distribute 4 over (x – 5). Simplify. Subtract 2 from both sides. The equation of the line through the point (5, – 2) that is parallel to the equation 8 x – 2 y = 6 is y = 4 x – 22. 14 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 1, continued This can be seen on the following graph. ✔ 15 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 1, continued 16 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice Example 3 Find the point on the line y = 4 x + 1 that is closest to the point (– 2, 8). 17 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 1. Find the line perpendicular to the given line, y = 4 x + 1, that passes through the point (– 2, 8). 18 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 2. Identify the slope of the given line. The slope of the line y = 4 x + 1 is 4. 19 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 3. Find the opposite reciprocal of the slope of the given line. The opposite of 4 is – 4. The reciprocal of – 4 is . 20 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 4. Substitute the opposite reciprocal for m in the point-slope form of a linear equation. y – y 1 = m(x – x 1) Point-slope form Substitute m from the given equation. 21 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 5. Substitute x and y from the given point into the equation for x 1 and y 1. Equation Substitute (– 2, 8) for x 1 and y 1. 22 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 6. Simplify the equation. Equation with substituted values for x 1 and y 1 Distribute (x – (– 2)). over Add 8 to both sides. 23 6. 1. 2: Working with Parallel and Perpendicular Lines
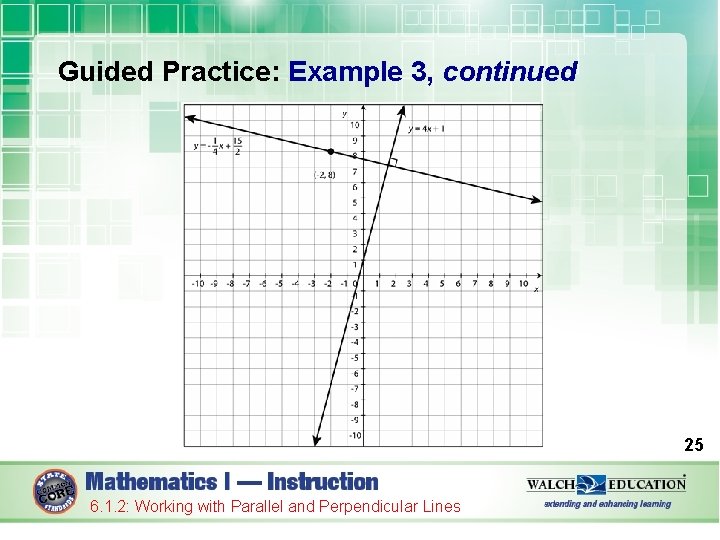
Guided Practice: Example 3, continued The equation of the line through the point (– 2, 8) that is perpendicular to the graph of y = 4 x + 1 is. This can be seen on the following graph. 24 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 25 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 7. Find the intersection between the two lines by setting the given equation equal to the equation of the perpendicular line, then solve for x. Set both equations equal to each other. Subtract 1 from both sides. 26 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued Add to both sides. Divide both sides by . 27 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 8. Substitute the value of x back into the given equation to find the value of y. y = 4 x + 1 Given equation Substitute for x. Simplify. 28 6. 1. 2: Working with Parallel and Perpendicular Lines
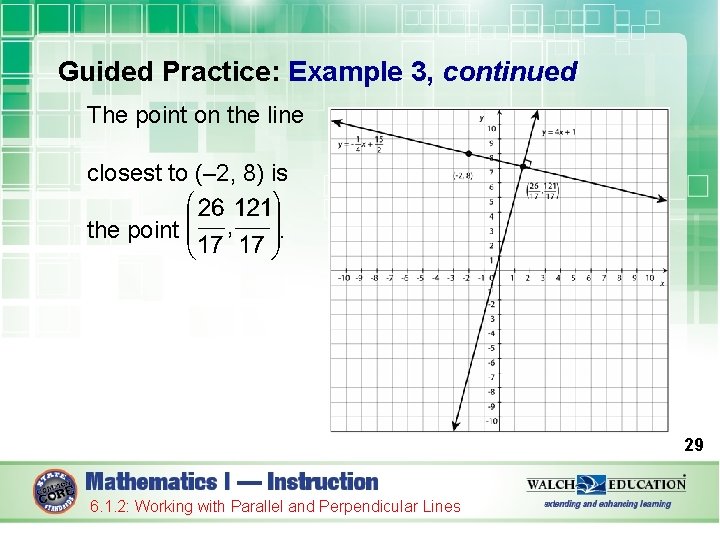
Guided Practice: Example 3, continued The point on the line closest to (– 2, 8) is the point . 29 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 9. Calculate the distance between the two points using the distance formula. Distance formula Substitute values for (x 1, y 1) and (x 2, y 2) using (– 2, 8) and 30 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued Simplify. Evaluate squares. Simplify. 31 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued Reduce to lowest terms. The distance between the point of intersection and the given point is units, or approximately 3. 6 units. ✔ 32 6. 1. 2: Working with Parallel and Perpendicular Lines
Guided Practice: Example 3, continued 33 6. 1. 2: Working with Parallel and Perpendicular Lines
Parallel lines slope
Antigentest åre
Rules for parallel and perpendicular lines
Parallel perpendicular or neither
Slopes of parallel and perpendicular lines assignment
Two lines are parallel if their slopes are
What slope is perpendicular to 5/8
Lesson 12-4 slopes of parallel and perpendicular lines
Slopes of parallel and perpendicular lines lesson 8-1
Lesson 2-4 slopes of parallel and perpendicular lines
Lesson 3-3 slopes of lines
Homework 5 slopes of lines
3-3 slopes of lines answer key
Find and use slopes of lines
Slopes of lines
What is a type line in fingerprint
Define parallel lines and intersecting lines
Low prices always
Magnetic field lines always cross.
In graphic communications outer lines are always
Type of slopes
Oversteepening of slopes
Parallel vs perpendicular
Structure of emigree
Tissue imtiaz dharker context
No slope
Constant slope
Intercept form
How to get the y intercept
Simple slopes analysis spss
The graceful slopes glow even clearer
Skradden slopes vista
Example of like forces
Parallelism
