Resultant of like and unlike parallel forces Parallel

Resultant of like and unlike parallel forces

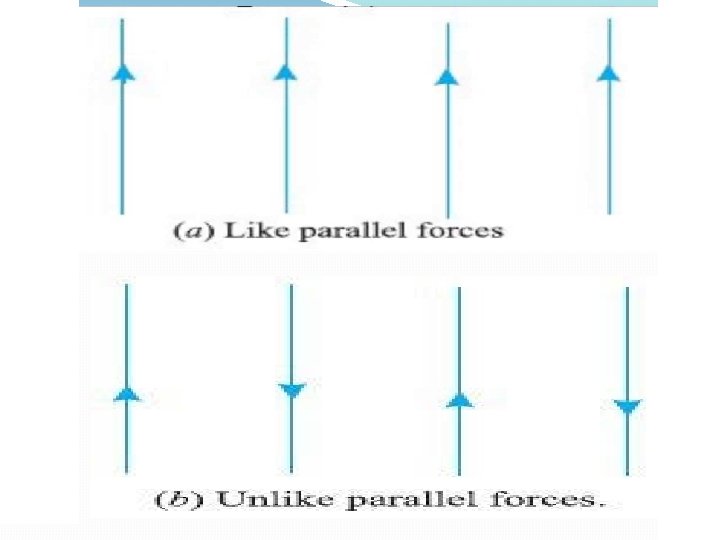
Parallel force The forces, whose line of action are parallel to each other, are known as parallel forces.

Classification of parallel forces Like parallel forces Unlike parallel forces Like parallel forces are forces that are parallel and act in the same direction. If there are two forces F 1 and F 2, then the resultant force R = F 1 + F 2. Unlike parallel forces are forces that are parallel and act in opposite directions. If there are two forces F 1 and F 2, then the resultant force R = -F 1 + F 2 where the negative force is the force acting in the downward direction.

Resultant force The resultant force is the single force that could be applied to an object (in this case, the rock), that would have the same effect as all the applied forces combined. Equation: R=ΣF=F 1+F 2+F 3+. . .

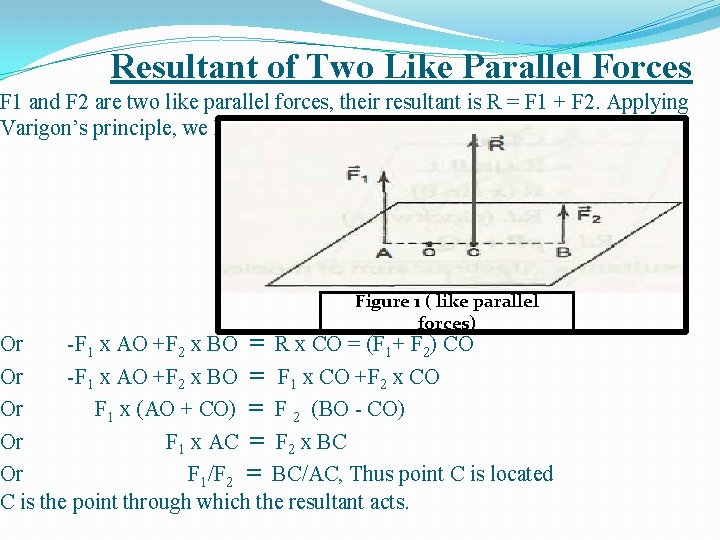
Resultant of Two Like Parallel Forces F 1 and F 2 are two like parallel forces, their resultant is R = F 1 + F 2. Applying Varigon’s principle, we have Figure 1 ( like parallel forces) Or -F 1 x AO +F 2 x BO = R x CO = (F 1+ F 2) CO Or -F 1 x AO +F 2 x BO = F 1 x CO +F 2 x CO Or F 1 x (AO + CO) = F 2 (BO - CO) Or F 1 x AC = F 2 x BC Or F 1/F 2 = BC/AC, Thus point C is located C is the point through which the resultant acts.

Resultant of Two Unlike Parallel Forces Applying the principle of moments about we get O- F l x AO – F 2 x BO = -R x CO = -R x CO Figure 1 ( like parallel forces) = – (F 1 -F 2) CO -F 1 x AO – F 2 x BO = – F 1 x CO + F 2 x CO F 1 (CO – AO) = F 2 (BO + CO) F 1 x AC = F 2 x BC F 1 /F 2 = BC/AC. This point C which is the application point of resultant is fixed.

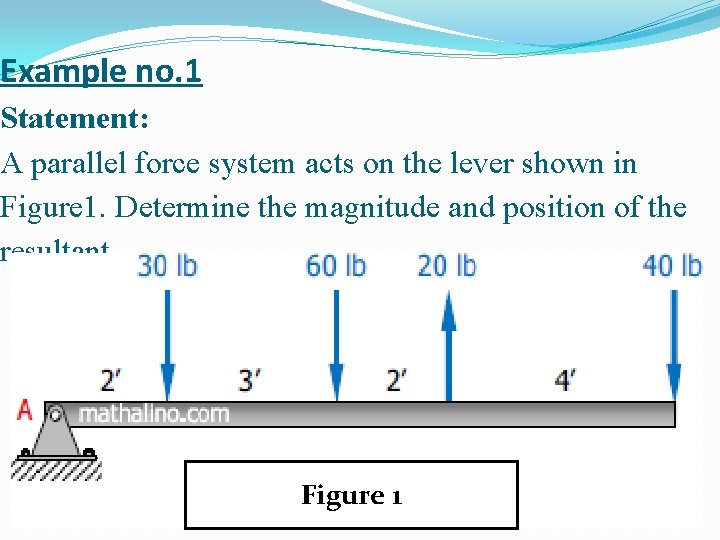
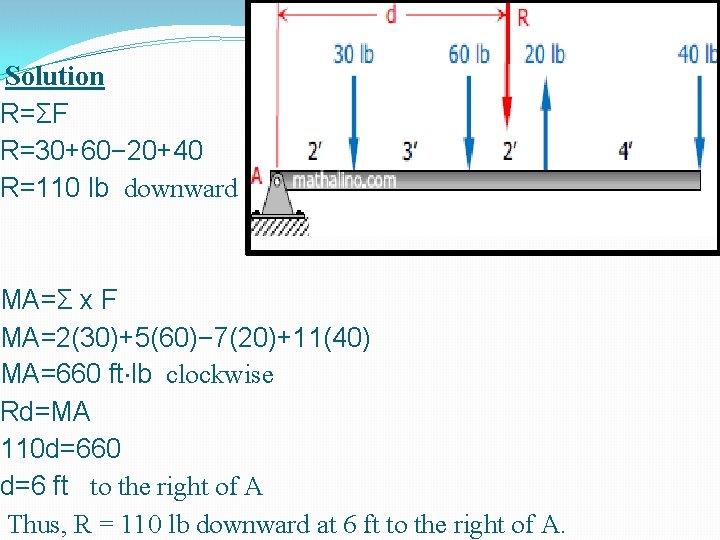
Example no. 1 Statement: A parallel force system acts on the lever shown in Figure 1. Determine the magnitude and position of the resultant. Figure 1

Solution R=ΣF R=30+60− 20+40 R=110 lb downward MA=Σ x F MA=2(30)+5(60)− 7(20)+11(40) MA=660 ft⋅lb clockwise Rd=MA 110 d=660 d=6 ft to the right of A Thus, R = 110 lb downward at 6 ft to the right of A.

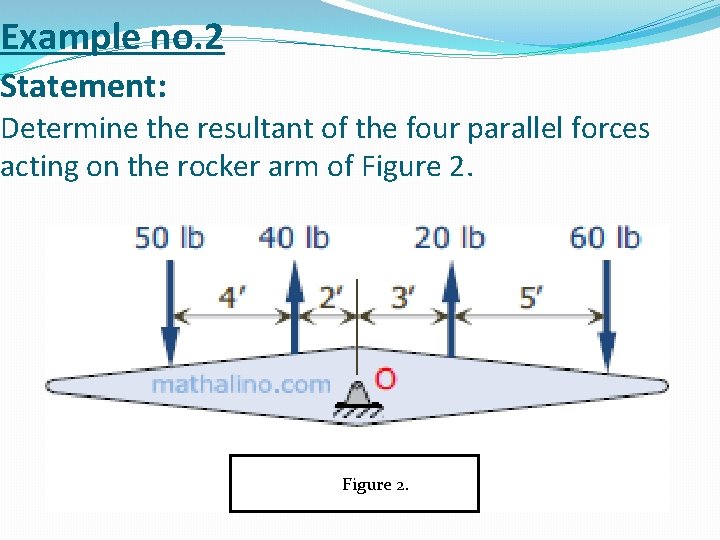
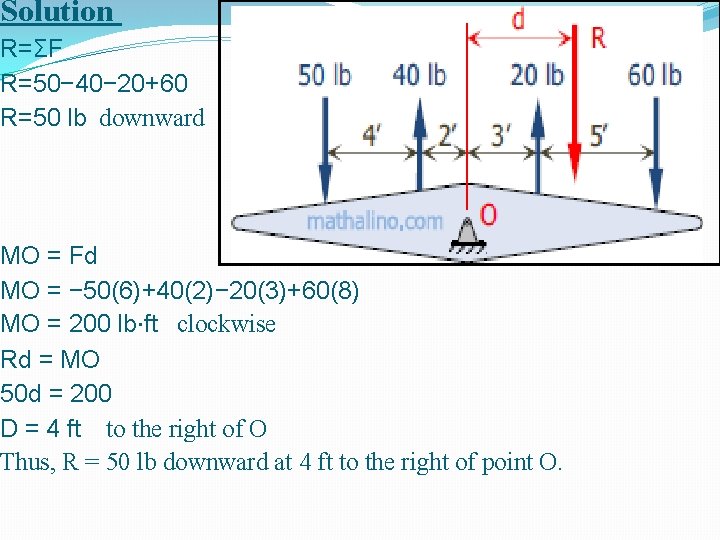
Example no. 2 Statement: Determine the resultant of the four parallel forces acting on the rocker arm of Figure 2. FFFHFigure 2.

Solution R=ΣF R=50− 40− 20+60 R=50 lb downward MO = Fd MO = − 50(6)+40(2)− 20(3)+60(8) MO = 200 lb⋅ft clockwise Rd = MO 50 d = 200 D = 4 ft to the right of O Thus, R = 50 lb downward at 4 ft to the right of point O.