Equations of Parallel and Perpendicular Lines ALGEBRA 1

Equations of Parallel and Perpendicular Lines ALGEBRA 1 UNIT 5: WRITING EQUATIONS OF LINES

Parallel Lines

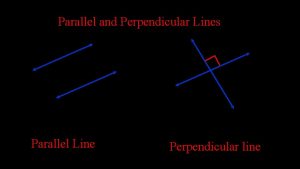
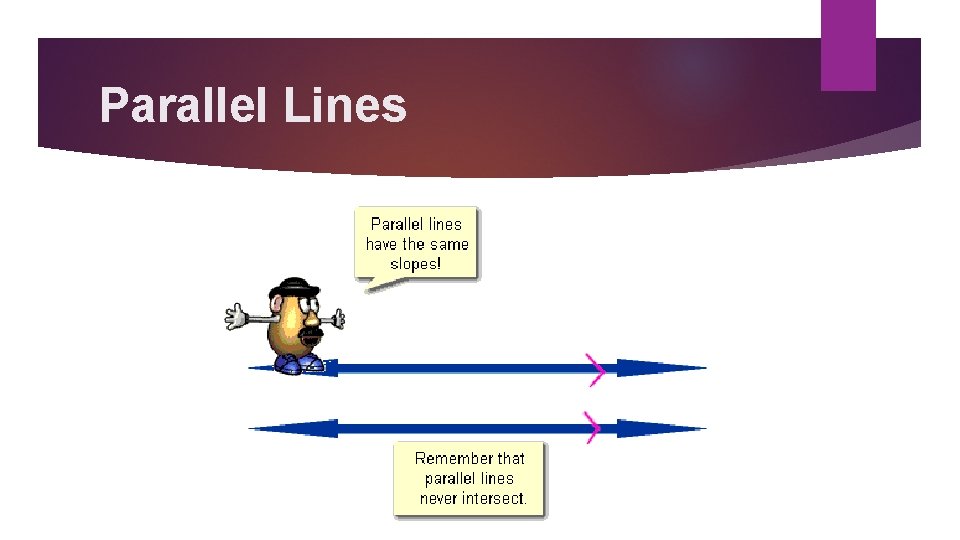
What are parallel lines? Parallel lines are two lines that never intersect each other.

Where have you seen examples in real-life? Lines on a road Lines between bricks Floor and ceiling Brainstorm as many examples of parallel lines as possible.

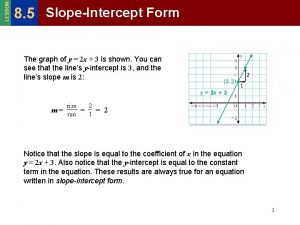
What characteristics do parallel lines have? Parallel lines are two lines that never intersect each other, BUT: What are their features on a graph? They have the same slope They can have different y- intercepts They still will never intersect

Parallel Lines

Determine if lines are parallel or perpendicular 1. Put the equation into slopeintercept form ( y = mx +b) 2. Determine if the slopes are the same (parallel) or opposite reciprocals (perpendicular) or neither.

Determine if the lines are parallel Y = 4 x + 16 Y = 3 x + 1 Y = -4 x – 1 Y = -1/4 x – 4 Y = 4 x - 2

Determine if two lines are parallel 2 x + 4 y = 10 9 x + 4 y = 12 Y = -9/4 x – 5 2 y = 18/4 x + 8 Y = - 3 x – 1

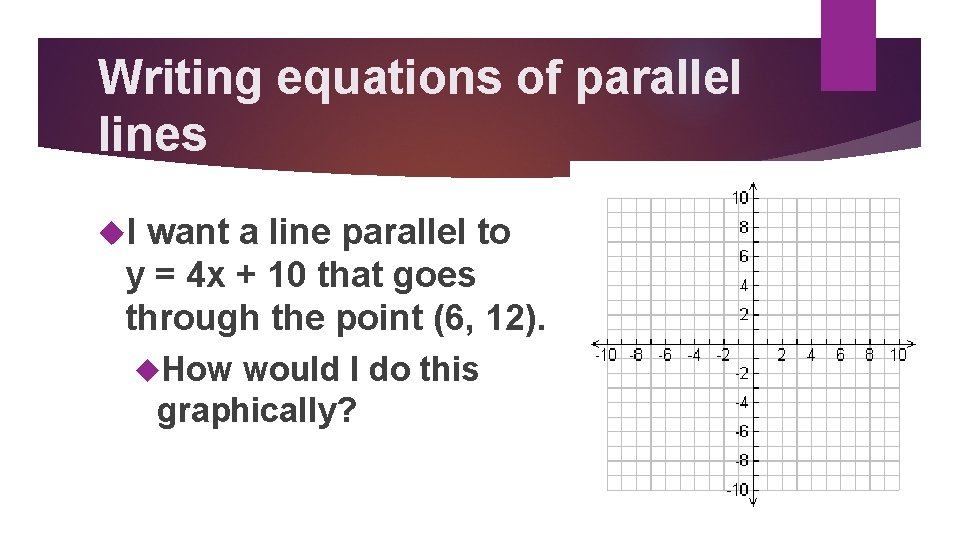
Writing equations of parallel lines I want a line parallel to y = 4 x + 10 that goes through the point (6, 12). How would I do this graphically?

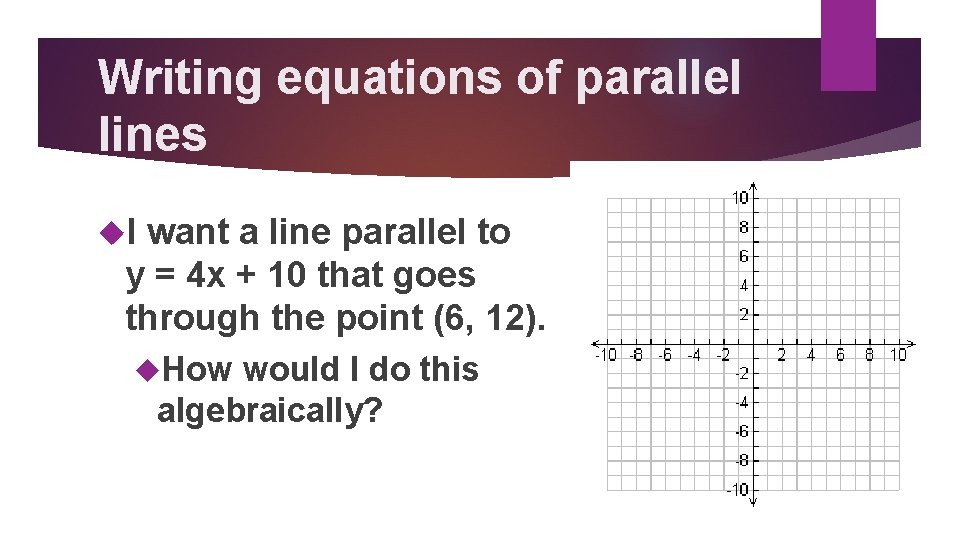
Writing equations of parallel lines I want a line parallel to y = 4 x + 10 that goes through the point (6, 12). How would I do this algebraically?

Example I want a line parallel to y = -2 x – 1 and through the point (3, 6).

Example I want a line parallel to y = 6 x + 12 and through the point (0, -10).

Real- Life Example I am creating a city which is to have two parallel streets. If I plot the first street such that the equation is y = 2 x – 2 and I want the other street to be 6 units away, what would be the equation of this street?

Real-Life Example

Questions?

Perpendicular Lines

What are perpendicular lines? Perpendicular lines are two lines that intersect to form a right angle. A right angle is an angle whose measure is 90 degrees.

Where have you seen examples in real-life? Floor and wall Intersection of two roads Tiles on the ground Brainstorm as many examples of parallel lines as possible.

What characteristics do perpendicular lines have? Perpendicular lines are two lines that intersect to form a right angle, BUT: What are their features on a graph? They have opposite reciprocal slopes WHY? They can have different y- intercepts

Perpendicular Lines

Determine if two lines are perpendicular x - 3 y = 10 9 x + 4 y = 12 Y = -9/4 x – 5 2 y = 18/4 x + 8 Y = - 3 x – 1

Write equations of perpendicular lines. I want a line perpendicular to y = 4 x + 10 that goes through the point (6, 12). How would I do this graphically?

Write equations of perpendicular lines. I want a line perpendicular to y = 4 x + 10 that goes through the point (6, 12). How would I do this algebraically?

Example I want a line perpendicular to = -2 x – 1 and through the point 6). y (3,

Example I want a line parallel to y = 6 x + 12 and through the point (0, -10).

Real- Life Example I am designing an intersection. I need the two streets to create a 90 degree angle. If the first street is located on the line y = 4 x – 2 where would I need to build the new road to create this intersection such that the road goes through a town located at a point (4, 7)?

Real- Life Example