Parallel and Perpendicular Lines Parallel and Perpendicular Lines

Parallel and Perpendicular Lines

Parallel and Perpendicular Lines • Perpendicular lines are two lines that intersect to form a 90 degree angle •

Parallel and Perpendicular Lines • Parallel lines are two lines that, if extended forever, would never cross or touch • In the figure below, line l is parallel to line m • (l // m ) l m

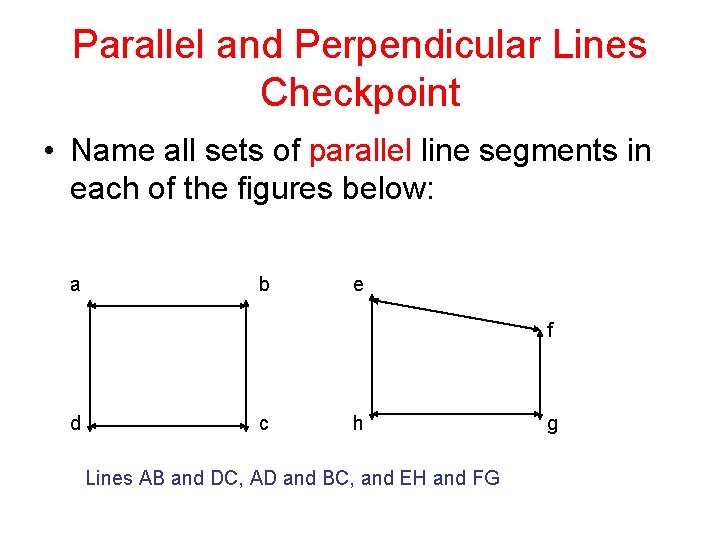
Parallel and Perpendicular Lines Checkpoint • Name all sets of parallel line segments in each of the figures below: a b e f d c h Lines AB and DC, AD and BC, and EH and FG g

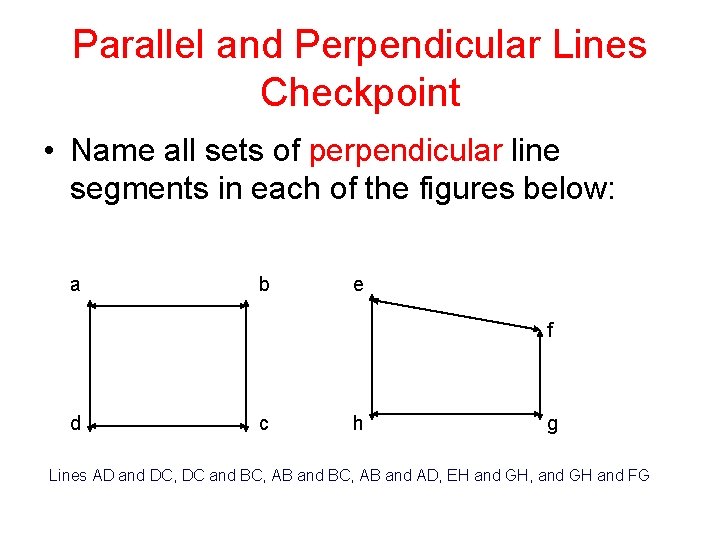
Parallel and Perpendicular Lines Checkpoint • Name all sets of perpendicular line segments in each of the figures below: a b e f d c h g Lines AD and DC, DC and BC, AB and AD, EH and GH, and GH and FG

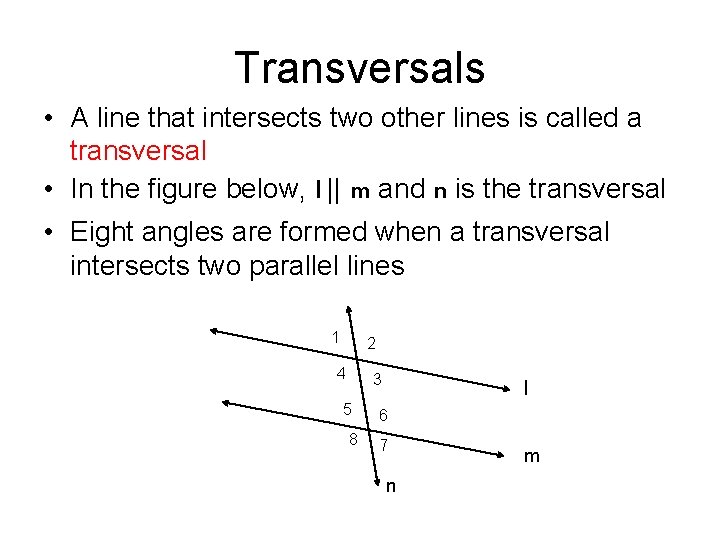
Transversals • A line that intersects two other lines is called a transversal • In the figure below, l || m and n is the transversal • Eight angles are formed when a transversal intersects two parallel lines 1 2 4 3 5 8 l 6 7 n m

Transversal Mini-Lab For this mini-lab, you will need: • Notebook paper • Pencil • Two colored pencils (share with neighbor) • Ruler (share with neighbor) • Protractor

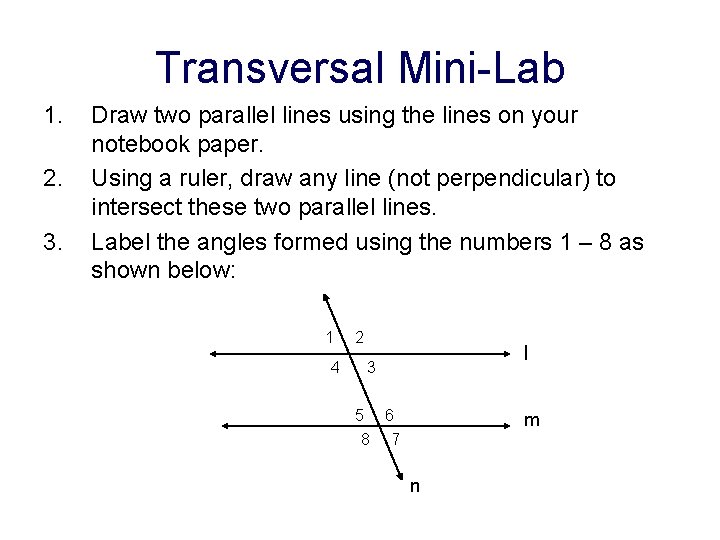
Transversal Mini-Lab 1. 2. 3. Draw two parallel lines using the lines on your notebook paper. Using a ruler, draw any line (not perpendicular) to intersect these two parallel lines. Label the angles formed using the numbers 1 – 8 as shown below: 1 4 2 l 3 5 6 8 7 m n

Transversal Mini-Lab 4. 5. 6. 7. Use a protractor to measure each angle and record it’s measurement below your figure (example: m 2 = 28 degrees) Shade angle 1 and each angle that has a congruent measurement with a colored pencil. Shade angle 2 and each angle that has a congruent measurement with another colored pencil. Compare your results with a neighbor and be prepared to discuss

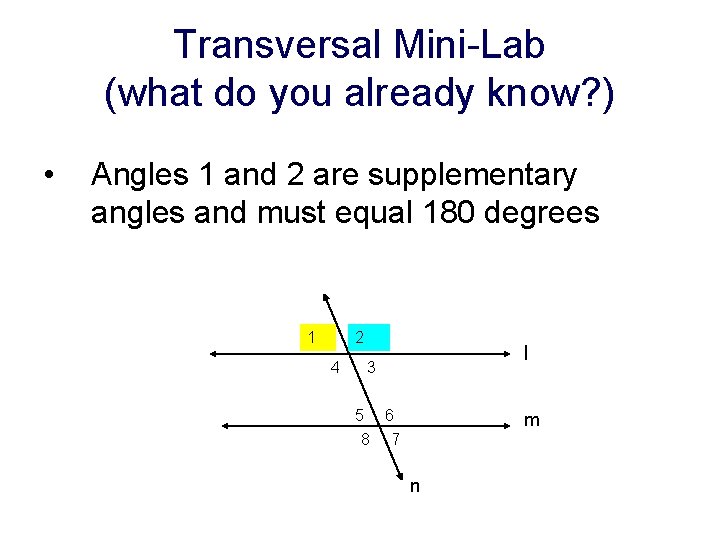
Transversal Mini-Lab (what do you already know? ) • Angles 1 and 2 are supplementary angles and must equal 180 degrees 1 2 4 l 3 5 6 8 7 m n

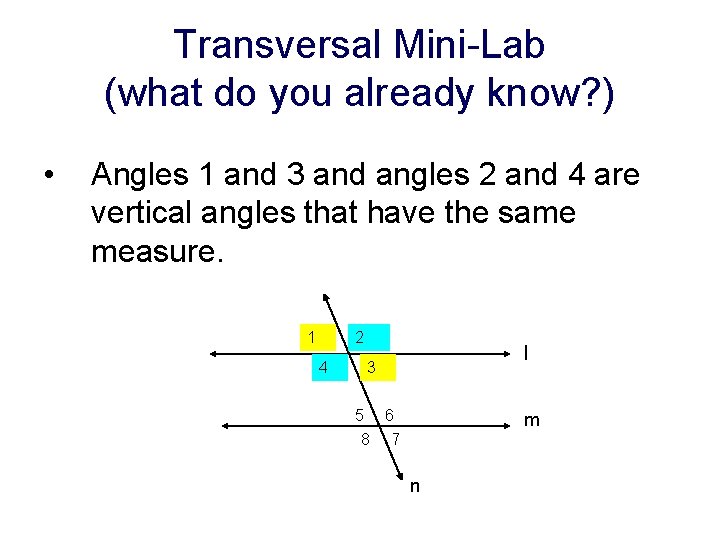
Transversal Mini-Lab (what do you already know? ) • Angles 1 and 3 and angles 2 and 4 are vertical angles that have the same measure. 1 2 4 l 3 5 6 8 7 m n

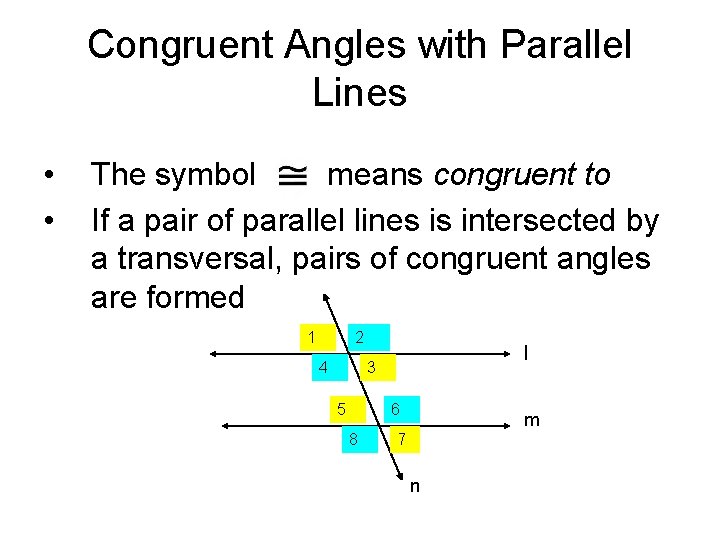
Congruent Angles with Parallel Lines • • The symbol means congruent to If a pair of parallel lines is intersected by a transversal, pairs of congruent angles are formed 1 2 4 l 3 5 6 8 m 7 n

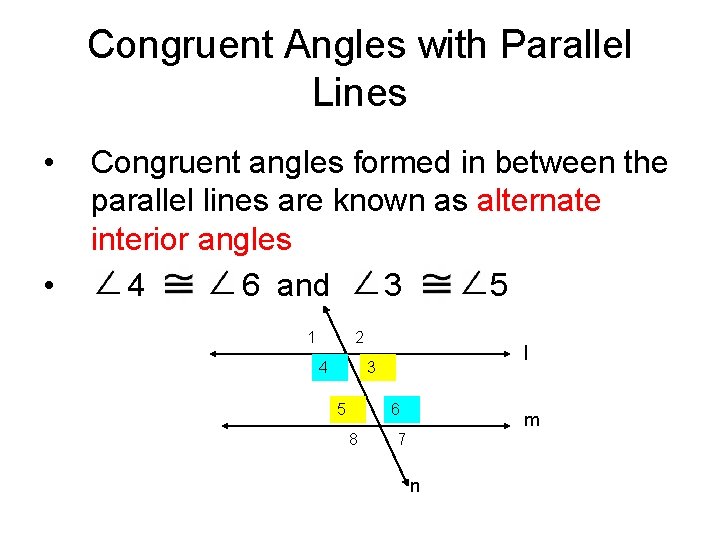
Congruent Angles with Parallel Lines • • Congruent angles formed in between the parallel lines are known as alternate interior angles 4 6 and 3 5 1 2 4 l 3 5 6 8 m 7 n

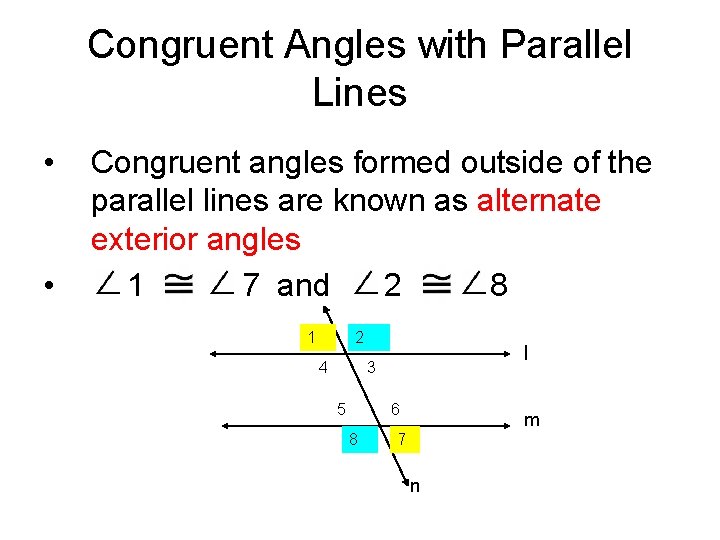
Congruent Angles with Parallel Lines • • Congruent angles formed outside of the parallel lines are known as alternate exterior angles 1 7 and 2 8 1 2 4 l 3 5 6 8 m 7 n

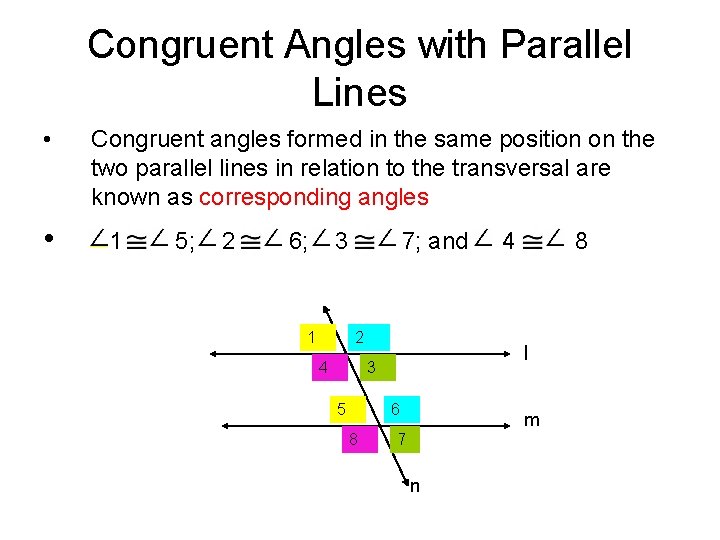
Congruent Angles with Parallel Lines • • Congruent angles formed in the same position on the two parallel lines in relation to the transversal are known as corresponding angles 1 5; 2 6; 3 1 7; and 2 4 6 8 8 l 3 5 4 m 7 n

Congruent Angles with Parallel Lines Checkpoint • In the figure below, m 1 = 65 • Explain how you find the measure of each of the rest of the angles using vocabulary words such as supplementary, vertical, corresponding, alternate interior, and alternate exterior angles n 1 2 4 5 8 l 3 6 7 m

Congruent Angles with Parallel Lines and Equations • In the figure below, m 1 = 11 x • m 6 = 5 x + 100 • Find the value of x and then find the measure of the remaining angles Hint: Angles 2 and 6 are Corresponding and angles 1 and 2 are Supplementary 1 2 4 3 5 8 l 6 7 m n

Homework • Skill 2: Parallel and Perpendicular Lines (both sides) • Practice 6 -1: Line and Angle Relationships (both sides) • Due Tomorrow!