and Perpendicular Lines 5 2 Parallel and Perpendicular

  • Slides: 21
Download presentation
and Perpendicular Lines 5 -2 Parallel and Perpendicular Lines Warm Up Problem of the

and Perpendicular Lines 5 -2 Parallel and Perpendicular Lines Warm Up Problem of the Day Lesson Presentation Pre-Algebra

5 -2 Parallel and Perpendicular Lines Warm Up Complete each sentence. 1. Angles whose

5 -2 Parallel and Perpendicular Lines Warm Up Complete each sentence. 1. Angles whose measures have a sum of 90° are ________. complementary 2. Vertical angles have equal measures, so they are congruent _______. 3. Angles whose measures have a sum of 180° are supplementary _______. 4. A part of a line between two points is called a segment ______. Pre-Algebra

5 -2 Parallel and Perpendicular Lines Problem of the Day The square root of

5 -2 Parallel and Perpendicular Lines Problem of the Day The square root of 1, 813, 141, 561 is a whole number. Is it odd or even? How do you know? An odd number can only be the product of two odd numbers. Since 1, 813, 141, 561 is an odd number, its square root is also an odd number. Pre-Algebra

5 -2 Parallel and Perpendicular Lines Learn to identify parallel and perpendicular lines and

5 -2 Parallel and Perpendicular Lines Learn to identify parallel and perpendicular lines and the angles formed by a transversal. Pre-Algebra

5 -2 Parallel and Perpendicular Lines Vocabulary parallel lines perpendicular lines transversal Pre-Algebra

5 -2 Parallel and Perpendicular Lines Vocabulary parallel lines perpendicular lines transversal Pre-Algebra

5 -2 Parallel and Perpendicular Lines Parallel lines are two lines in a plane

5 -2 Parallel and Perpendicular Lines Parallel lines are two lines in a plane that never meet, like a set of perfectly straight, infinite train tracks. Perpendicular lines are lines that intersect at 90° angles. Pre-Algebra

5 -2 Parallel and Perpendicular Lines The railroad ties are transversals to the tracks.

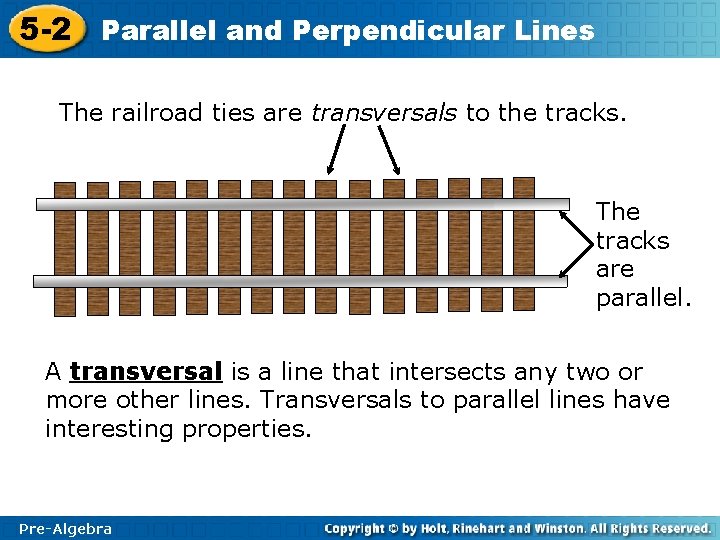
5 -2 Parallel and Perpendicular Lines The railroad ties are transversals to the tracks. The tracks are parallel. A transversal is a line that intersects any two or more other lines. Transversals to parallel lines have interesting properties. Pre-Algebra

5 -2 Parallel and Perpendicular Lines Additional Example 1: Identifying Congruent Angles Formed by

5 -2 Parallel and Perpendicular Lines Additional Example 1: Identifying Congruent Angles Formed by a Transversal Measure the angles formed by the transversal and parallel lines. Which angles seem to be congruent? 1, 3, 5, and 7 all measure 150°. 2, 4, 6, and 8 all measure 30°. Pre-Algebra

5 -2 Parallel and Perpendicular Lines Additional Example 1 Continued Angles marked in blue

5 -2 Parallel and Perpendicular Lines Additional Example 1 Continued Angles marked in blue appear to be congruent to each other, and angles marked in red appear to be congruent to each other. 1 @ 3 @ 5 @ 7 2 @ 4 @ 6 @ 8 Pre-Algebra 2 1 3 4 6 5 7 8

5 -2 Parallel and Perpendicular Lines Try This 1: Example 1 Measure the angles

5 -2 Parallel and Perpendicular Lines Try This 1: Example 1 Measure the angles formed by the transversal and parallel lines. Which angles seem to be congruent? 1 2 3 4 5 6 7 8 1, 4, 5, and 8 all measure 36°. 2, 3, 6, and 7 all measure 144°. Pre-Algebra

5 -2 Parallel and Perpendicular Lines Try This 1: Example 1 Continued Angles marked

5 -2 Parallel and Perpendicular Lines Try This 1: Example 1 Continued Angles marked in blue appear to be congruent to each other, and angles marked in red appear to be congruent to each other. 1 @ 4 @ 5 @ 8 2 @ 3 @ 6 @ 7 1 Pre-Algebra 2 3 4 5 6 7 8

5 -2 Parallel and Perpendicular Lines PROPERTIES OF TRANSVERSALS TO PARALLEL LINES If two

5 -2 Parallel and Perpendicular Lines PROPERTIES OF TRANSVERSALS TO PARALLEL LINES If two parallel lines are intersected by a transversal, • the acute angles that are formed are all congruent, • the obtuse angles are all congruent, • and any acute angle is supplementary to any obtuse angle. If the transversal is perpendicular to the parallel lines, all of the angles formed are congruent 90° angles. Pre-Algebra

5 -2 Parallel and Perpendicular Lines Writing Math The symbol for parallel is ||.

5 -2 Parallel and Perpendicular Lines Writing Math The symbol for parallel is ||. The symbol for perpendicular is . Pre-Algebra

5 -2 Parallel and Perpendicular Lines Additional Example 2 A: Finding Angle Measures of

5 -2 Parallel and Perpendicular Lines Additional Example 2 A: Finding Angle Measures of Parallel Lines Cut by Transversals In the figure, line l || line m. Find the measure of the angle. A. 4 All obtuse angles in the figure are congruent. m 4 = 124° Pre-Algebra

5 -2 Parallel and Perpendicular Lines Additional Example 2 B: Finding Angle Measures of

5 -2 Parallel and Perpendicular Lines Additional Example 2 B: Finding Angle Measures of Parallel Lines Cut by Transversals Continued In the figure, line l || line m. Find the measure of the angle. B. 2 2 is supplementary to the angle 124°. m 2 + 124° = 180° – 124° m 2 = 56° Pre-Algebra

5 -2 Parallel and Perpendicular Lines Additional Example 2 C: Finding Angle Measures of

5 -2 Parallel and Perpendicular Lines Additional Example 2 C: Finding Angle Measures of Parallel Lines Cut by Transversals Continued In the figure, line l || line m. Find the measure of the angle. C. 6 All acute angles in the figure are congruent. m 6 = 56° Pre-Algebra

5 -2 Parallel and Perpendicular Lines Try This: Example 2 A In the figure,

5 -2 Parallel and Perpendicular Lines Try This: Example 2 A In the figure, line n || line m. Find the measure of the angle. A. 7 All obtuse angles in the figure are congruent m 7 = 144° Pre-Algebra 1 144° 3 4 5 6 7 8 m n

5 -2 Parallel and Perpendicular Lines Try This: Example 2 B In the figure,

5 -2 Parallel and Perpendicular Lines Try This: Example 2 B In the figure, line n || line m. Find the measure of the angle. B. 5 5 is supplementary to the angle 144°. m 5 + 144° = 180° – 144° m 5 = 36° Pre-Algebra 1 144° 3 4 5 6 7 8 m n

5 -2 Parallel and Perpendicular Lines Try This: Example 2 C In the figure,

5 -2 Parallel and Perpendicular Lines Try This: Example 2 C In the figure, line n || line m. Find the measure of the angle. C. 1 All acute angles in the figure are congruent m 1 = 36° Pre-Algebra 1 144° 3 4 5 6 7 8 m n

5 -2 Parallel and Perpendicular Lines If two lines are intersected by a transversal

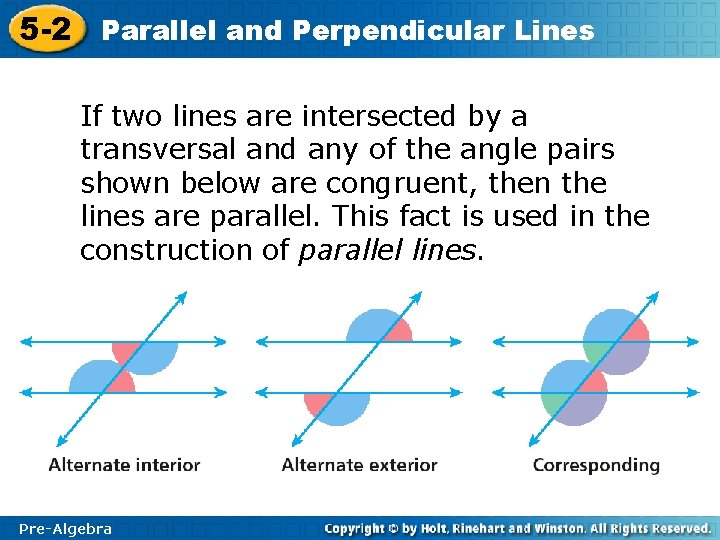
5 -2 Parallel and Perpendicular Lines If two lines are intersected by a transversal and any of the angle pairs shown below are congruent, then the lines are parallel. This fact is used in the construction of parallel lines. Pre-Algebra

5 -2 Parallel and Perpendicular Lines Lesson Quiz In the figure a || b.

5 -2 Parallel and Perpendicular Lines Lesson Quiz In the figure a || b. 1. Name the angles congruent to 3. 1, 5, 7 2. Name all the angles supplementary to 6. 1, 3, 5, 7 3. If m 1 = 105° what is m 3? 105° 4. If m 5 = 120° what is m 2? 60° Pre-Algebra

Parallel and Perpendicular Lines Parallel and Perpendicular LinesParallel and Perpendicular Lines Parallel and Perpendicular Lines
Parallel Perpendicular Lines Parallel and Perpendicular Lines TheParallel Perpendicular Lines Parallel and Perpendicular Lines The
Parallel and Perpendicular Lines Parallel Lines Two linesParallel and Perpendicular Lines Parallel Lines Two lines
Parallel and Perpendicular Assignment Parallel Lines Parallel linesParallel and Perpendicular Assignment Parallel Lines Parallel lines
Parallel and Perpendicular Lines Parallel Line Perpendicular lineParallel and Perpendicular Lines Parallel Line Perpendicular line
PARALLEL AND PERPENDICULAR LINES Slopes Parallel Lines ThePARALLEL AND PERPENDICULAR LINES Slopes Parallel Lines The
Parallel and Perpendicular Lines Slope of Parallel LinesParallel and Perpendicular Lines Slope of Parallel Lines
Parallel and Perpendicular Lines Objectives Define parallel linesParallel and Perpendicular Lines Objectives Define parallel lines
Parallel Perpendicular Lines Parallel and Lines Transversals ReviewParallel Perpendicular Lines Parallel and Lines Transversals Review
Parallel and Perpendicular Lines Parallel Lines l AllParallel and Perpendicular Lines Parallel Lines l All
Parallel and Perpendicular Lines Parallel Lines Two nonverticalParallel and Perpendicular Lines Parallel Lines Two nonvertical
Parallel Perpendicular Lines Slope of Parallel Lines TwoParallel Perpendicular Lines Slope of Parallel Lines Two
Slopesofof Paralleland and Perpendicular Slopes Lines Perpendicular LinesSlopesofof Paralleland and Perpendicular Slopes Lines Perpendicular Lines
Slopesofof Paralleland and Perpendicular Slopes Lines Perpendicular LinesSlopesofof Paralleland and Perpendicular Slopes Lines Perpendicular Lines
3 4 Perpendicular Lines 3 4 Perpendicular Lines3 4 Perpendicular Lines 3 4 Perpendicular Lines
03032021 03032021 Perpendicular Lines Perpendicular lines meet at03032021 03032021 Perpendicular Lines Perpendicular lines meet at
Pairs of Lines 1 Parallel Lines Parallel linesPairs of Lines 1 Parallel Lines Parallel lines
Parallel Lines Introduction What are parallel lines LinesParallel Lines Introduction What are parallel lines Lines
PARALLEL LINES TRANSVERSALS PARALLEL LINES ARE LINES THATPARALLEL LINES TRANSVERSALS PARALLEL LINES ARE LINES THAT
Parallel lines Perpendicular lines and line segments ByParallel lines Perpendicular lines and line segments By