Parallel and Perpendicular Lines Objectives Define parallel lines

Parallel and Perpendicular Lines Objectives: Define parallel lines. Find equations of parallel lines. Define perpendicular lines Find equations of perpendicular lines.

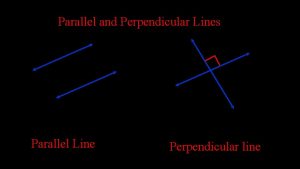
Parallel Lines • Slopes of parallel lines are equal. • Recall the steps of finding an equation of a line. – Find slope – Find the y-intercept – Write the equation – This is the same process when working with parallel and perpendicular lines.

Find an equation of a line passing through (-2, 5) that is parallel to 3 x + 2 y = 9 • Find slope: – Get y by itself in the given equation 2 y = 9 – 3 x y = 9/2 – 3/2 x slope=-3/2 • Find y-intercept: – Use a slope of -3/2 since the lines are parallel y = -3/2 x + b 5 = -3/2 (-2) + b 5=3+b 2=b • Write equation: y = -3/2 x + 2

Perpendicular Lines • Perpendicular lines have negative reciprocal slopes. • If a line has a slope of -1/2 the perpendicular line would have a slope of 2. • If a line has a slope of 5/6 the perpendicular line would have a slope of -6/5 • What would be the slope of a line perpendicular to a line with a slope of -7? 1/7

Find the equation of the line passing through (-1, 3) that is perpendicular to 3 x – 2 y = 8. 1. Find slope 1. Get y by itself: -2 y = 8 – 3 x y = -4 + 3/2 x 2. Slope is 3/2 so perpendicular slope is 2/3 2. Find y-intercept 1. y = -2/3 x + b 3 = (-2/3)(-1) + b 3 = 2/3 + b 3 – 2/3 = b 7/3 =b 3. Write equation y = -2/3 x + 7/3

Review concepts learned • Parallel lines have equal slope • Perpendicular lines have negative reciprocal slopes. • To find an equation of a line – Find slope – Find y-intercept – Write equation

Assignment • Page 197 • #7, 11, 13, 17, 21, 23, 25, 29, 33, 37
- Slides: 7