Chapter 3 Parallel and Perpendicular Lines Lesson 1

Chapter 3: Parallel and Perpendicular Lines Lesson 1: Parallel Lines and Transversals

Definitions Parallel lines ( || )- coplanar lines that do not intersect (arrows on lines indicate which sets are parallel to each other) p Parallel planes- two or more planes that do not intersect p Skew lines- lines that do not intersect but are not parallel (are not coplanar) p Transversal- a line that intersects two or more lines in a plane at different points p

Pairs of angles formed by parallel lines and a transversal (see graphic organizer for examples) p p p p Exterior angles: outside the two parallel lines Interior angles: between the two parallel lines Consecutive Interior angles: between the two parallel lines, on the same side of the transversal Consecutive Exterior angles: outside the two parallel lines, on the same side of the transversal Alternate Exterior angles: outside the two parallel lines, on different sides of the transversal Alternate Interior angles: between the two parallel lines, on different sides of the transversal Corresponding angles: one outside the parallel lines, one inside the parallel lines and both on the same side of the transversal

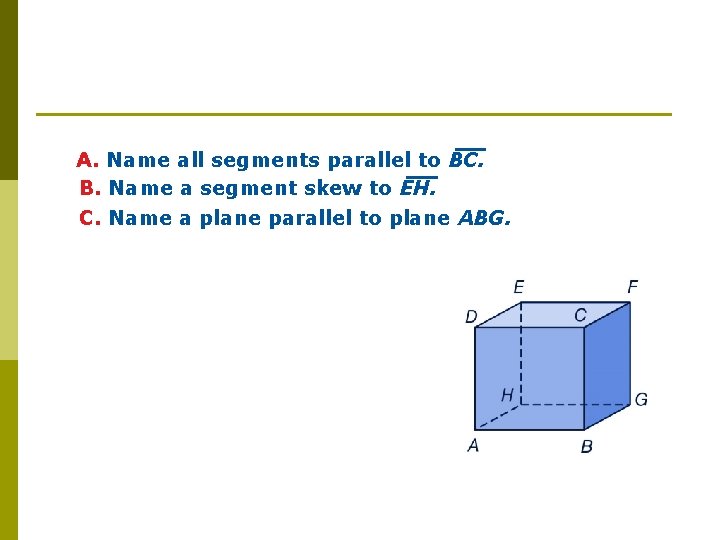
A. Name all segments parallel to BC. B. Name a segment skew to EH. C. Name a plane parallel to plane ABG.

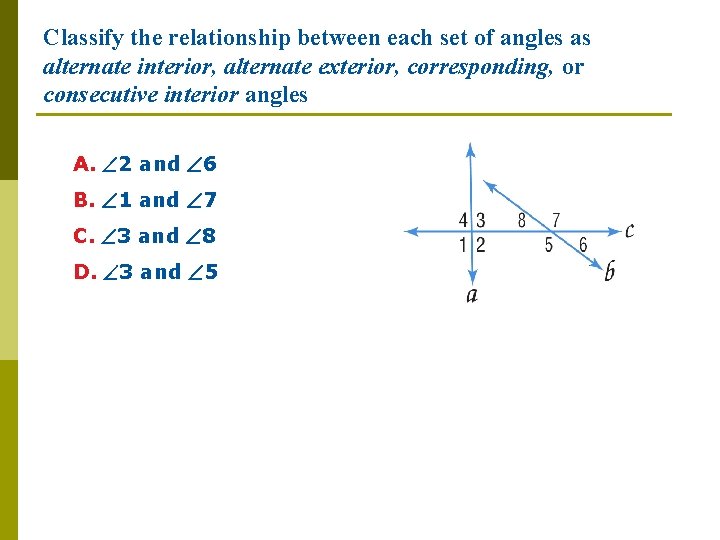
Classify the relationship between each set of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles A. 2 and 6 B. 1 and 7 C. 3 and 8 D. 3 and 5

A. Identify the sets of lines to which line a is a transversal. B. Identify the sets of lines to which line b is a transversal. C. Identify the sets of lines to which line c is a transversal.

Chapter 3: Parallel and Perpendicular Lines Lesson 2: Angles and Parallel Lines

If two parallel lines are cut by a transversal, then… (see graphic organizer) the alternate interior angles are congruent p the consecutive interior angles are supplementary p the alternate exterior angles are congruent p the corresponding angles are congruent p p In a plane, if a line is perpendicular to one of the two parallel lines, then it is also perpendicular to the other line.

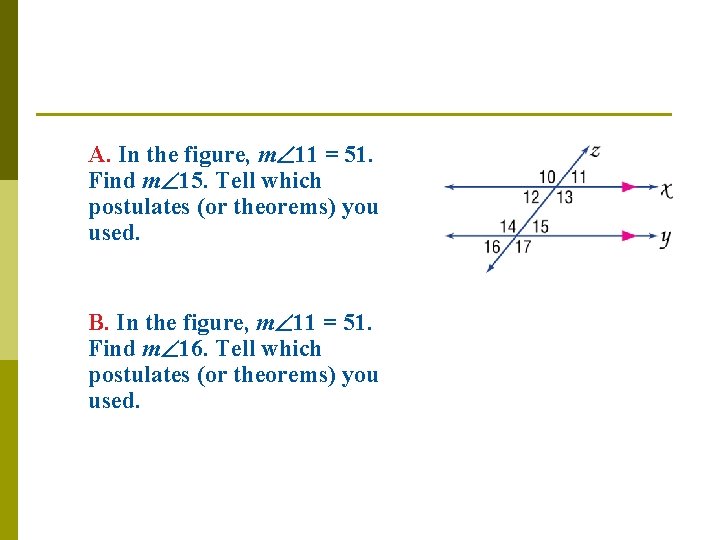
A. In the figure, m 11 = 51. Find m 15. Tell which postulates (or theorems) you used. B. In the figure, m 11 = 51. Find m 16. Tell which postulates (or theorems) you used.

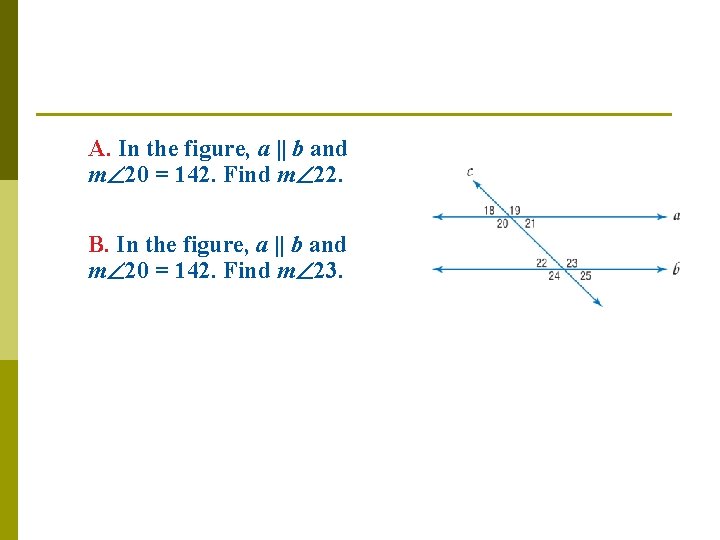
A. In the figure, a || b and m 20 = 142. Find m 22. B. In the figure, a || b and m 20 = 142. Find m 23.

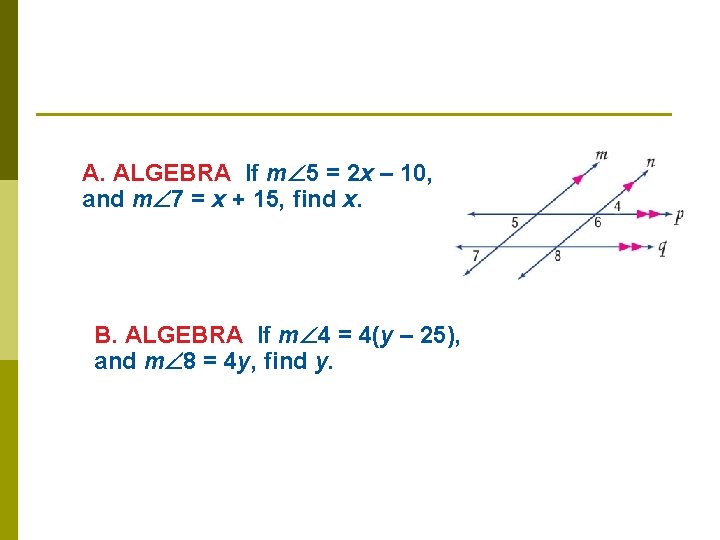
A. ALGEBRA If m 5 = 2 x – 10, and m 7 = x + 15, find x. B. ALGEBRA If m 4 = 4(y – 25), and m 8 = 4 y, find y.

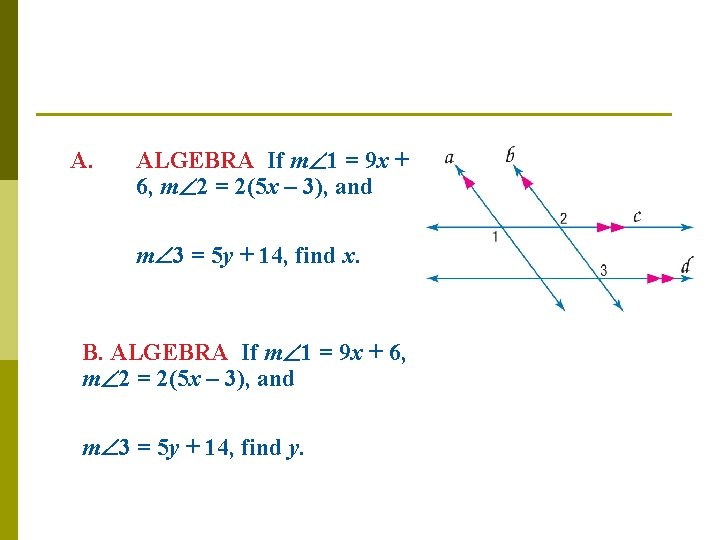
A. ALGEBRA If m 1 = 9 x + 6, m 2 = 2(5 x – 3), and m 3 = 5 y + 14, find x. B. ALGEBRA If m 1 = 9 x + 6, m 2 = 2(5 x – 3), and m 3 = 5 y + 14, find y.

Chapter 3: Parallel and Perpendicular Lines Lesson 5: Proving Lines Parallel

If… p p p (see graphic organizer) Corresponding angles are congruent, Alternate exterior angles are congruent, Consecutive interior angles are supplementary, Alternate interior angles are congruent, Two lines are both perpendicular to the transversal, Then the lines are parallel. p If given a line and a point not on the line, there is exactly one line through that point that is parallel to the given line

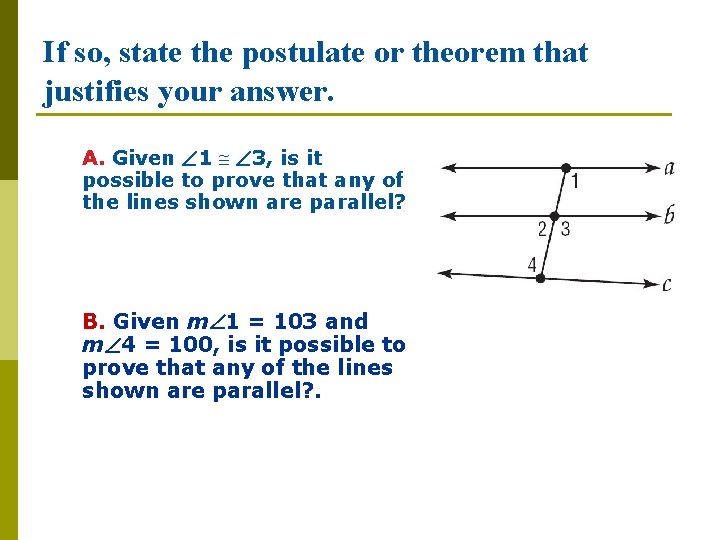
If so, state the postulate or theorem that justifies your answer. A. Given 1 3, is it possible to prove that any of the lines shown are parallel? B. Given m 1 = 103 and m 4 = 100, is it possible to prove that any of the lines shown are parallel? .

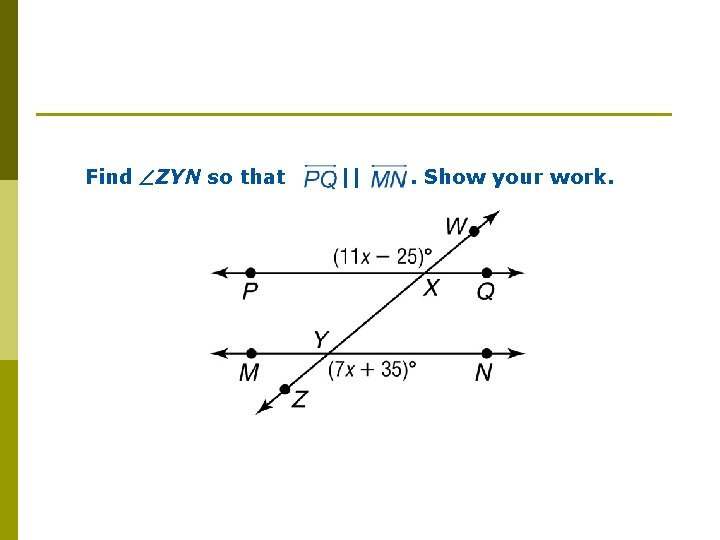
Find ZYN so that || . Show your work.

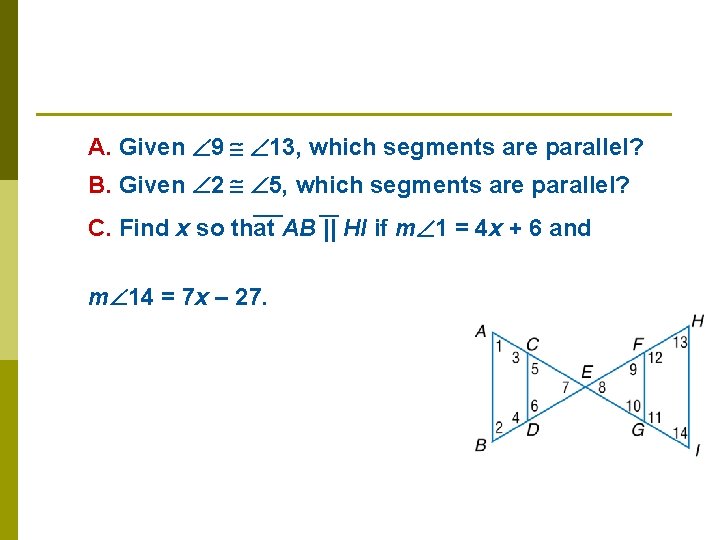
A. Given 9 13, which segments are parallel? B. Given 2 5, which segments are parallel? ___ __ C. Find x so that AB || HI if m 1 = 4 x + 6 and m 14 = 7 x – 27.

Chapter 3: Parallel and Perpendicular Lines Lesson 3: Slopes of Lines

Slope The ratio of the vertical rise over the horizontal run p Can be used to describe a rate of change p Two non-vertical lines have the same slope if and only if they are parallel p Two non-vertical lines are perpendicular if and only if the product of their slopes is -1 p

Foldable p Step 1: fold the paper into 3 columns/sections p Step 2: fold the top edge down about ½ inch to form a place for titles. Unfold the paper and turn it vertically. Step 3: title the top row “Slope”, the middle row “Slopeintercept form” and the bottom row “Point-slope form” p

Slope Rise = 0 Run = 0 zero slope (horizontal line) undefined (vertical line) Parallel = same slope Perpendicular = one slope is the reciprocal and opposite sign of the other Ex: find the slope of a line containing (4, 6) and (-2, 8)

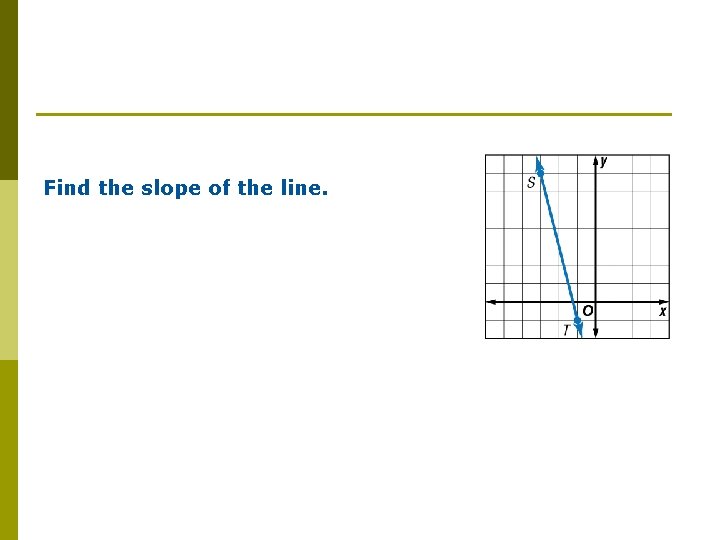
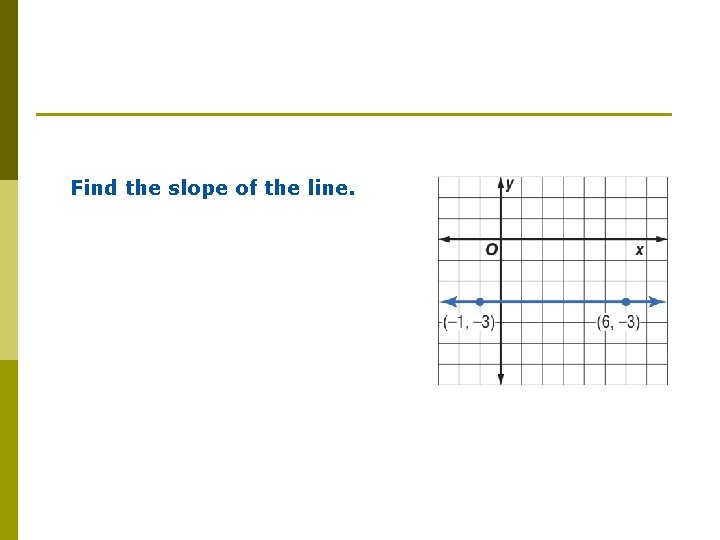
Find the slope of the line.

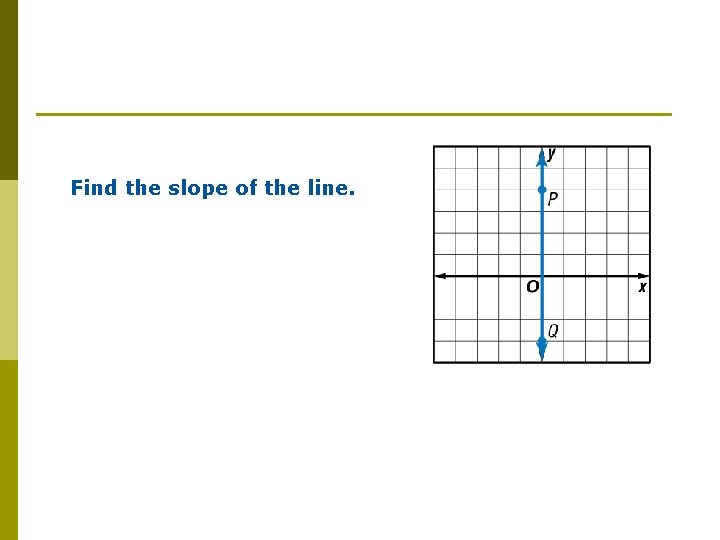
Find the slope of the line.

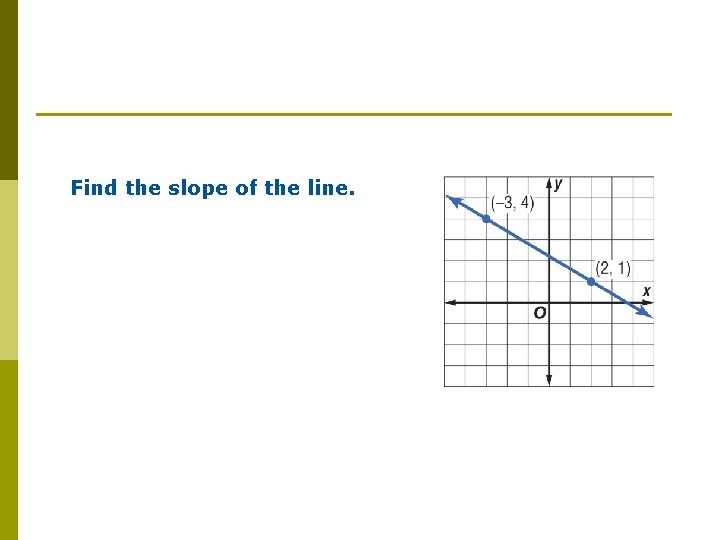
Find the slope of the line.

Find the slope of the line.

Determine whether FG and HJ are parallel, perpendicular, or neither for F(1, – 3), G(– 2, – 1), H(5, 0), and J(6, 3). (DO NOT GRAPH TO FIGURE THIS OUT!!) p

p Determine whether AB and CD are parallel, perpendicular, or neither for A(– 2, – 1), B(4, 5), C(6, 1), and D(9, – 2)

A. Graph the line that contains Q(5, 1) and is parallel to MN with M(– 2, 4) and N(2, 1). B. Graph the line that contains (-1, -3) and is perpendicular to MN for M(– 3, 4) and N(5, – 8)?

Chapter 3: Parallel and Perpendicular Lines Lesson 4: Equations of Lines

Slope-intercept form +b : y = mx Slope and y-intercept Two ordered-pairs (one is y-intercept) Two ordered-pairs (neither is y-intercept) m = -4 y-intercept = 7 (4, 1) (0, -2) (3, 3) (2, 0) * This should be your middle row on the foldable

Point-slope form: Slope and one ordered-pair m= (7, 2) Two ordered-pairs (8, -2) * This should be your bottom row on the foldable (-3, -1)

Write an equation in slope-intercept form of the line with slope of 6 and yintercept of – 3.

Write the equation in slope-intercept form and then Write an equation in point-slope form of the line whose slope is graph the line. that contains (– 10, 8). Then

Write an equation in slope-intercept form for a line containing (4, 9) and ( – 2, 0).

Write an equation in point-slope form for a line containing (– 3, – 7) and (– 1, 3).

On the back:

Chapter 3: Parallel and Perpendicular Lines Lesson 6: Distance Between Parallel Lines

Perpendicular Lines and Distance p p The shortest distance between a line and a point not on the line is the length of the perpendicular line connecting them Equidistant: the same distance- parallel lines are equidistant because they never get any closer or farther apart The distance between two parallel lines is the distance between one line and any point on the other line In a plane, if two lines are equidistant from a third line, then the two lines are parallel to each other

Steps to find the distance between parallel lines: 1. 2. 3. 4. 5. Change the first equation so that the slope is now perpendicular to the given slope. (do not change anything else) Set the new equation equal to the second given equation Solve for x. Plug in for x in the new equation (the one with the perpendicular slope) and solve for y. Find the distance between the ordered pair created with x and y and the y-intercept from the changed equation (the one with perpendicular slope).

p Find the distance between each pair of lines n n y = 2 x + 1 y = 2 x - 4

p Find the distance between the two parallel lines n n y= y= x+2 x-