Parallel and Perpendicular Lines Parallel Lines l All

Parallel and Perpendicular Lines

Parallel Lines // l All parallel lines have the same slope. l Parallel lines will NEVER have the same y-intercept. l The slope of all vertical lines is undefined. (No Slope) l The slope of all horizontal lines is zero.

Perpendicular Lines l Lines that form a 90° Angle. l Perpendicular Lines CAN have the same y-intercept IF that is where they cross. l Perpendicular Lines have slopes that are negative reciprocals. – This means to change the sign and flip the slope. Ex. If line “m” has a slope of 5, then it’s negative reciprocal is

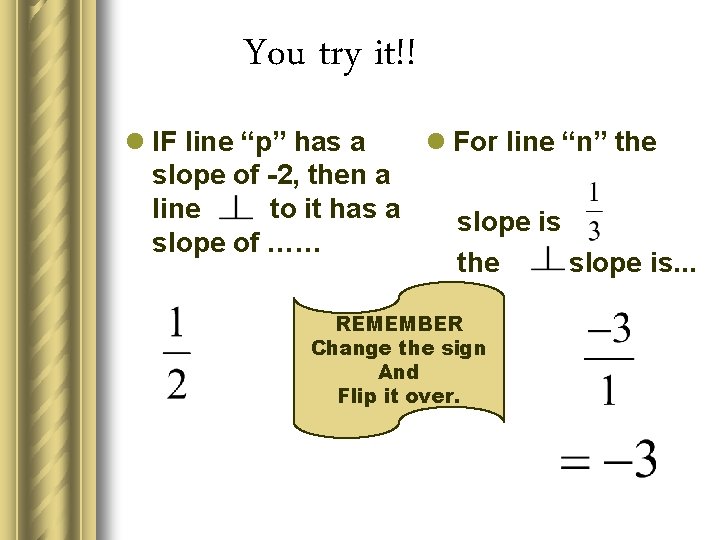
You try it!! l IF line “p” has a l For line “n” the slope of -2, then a line to it has a slope is slope of …… the slope is. . . REMEMBER Change the sign And Flip it over.

Let’s compare Vertical and Horizontal Lines. l Vertical lines are ┴ to horizontal lines. AND l Horizontal lines are ┴ to vertical lines.

Examples

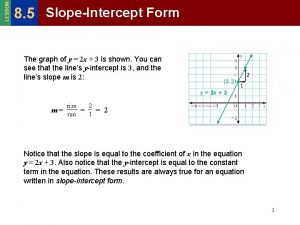
Name the slope of each line, then Give the PARALLEL slope and the PERPENDICULAR slope. Equation y = 3 x + 5 7 x + y = 4 y=2 x = -4 m // m m

Why do we need to be able to identify the Parallel & Perpendicular Slopes? l So that we can write equations for new lines. – Either lines that are Parallel – OR lines that are Perpendicular

l HOW? – 1. Name the slope of the line you are given. – 2. List the new slope. – 3. Use the new slope and the point you are given in the slope-intercept formula to write a new equation. Write an equation that is PARALLEL to the given line passing through the given point. Example 5 5. New // Equation

Write an equation that is PARALLEL to the given line passing through the given point. Example 6 6. To get the Slope, solve For “y” • Find the PRGM key on your calculator. • Select program ASLOPE • Which option? • #2 because you have a point and a slope. • Enter NEW (parallel) slope Parallel Lines Have SAME Slope (m) • Enter X and Y from your ordered pair But… DIFFERENT Y-int. (b)

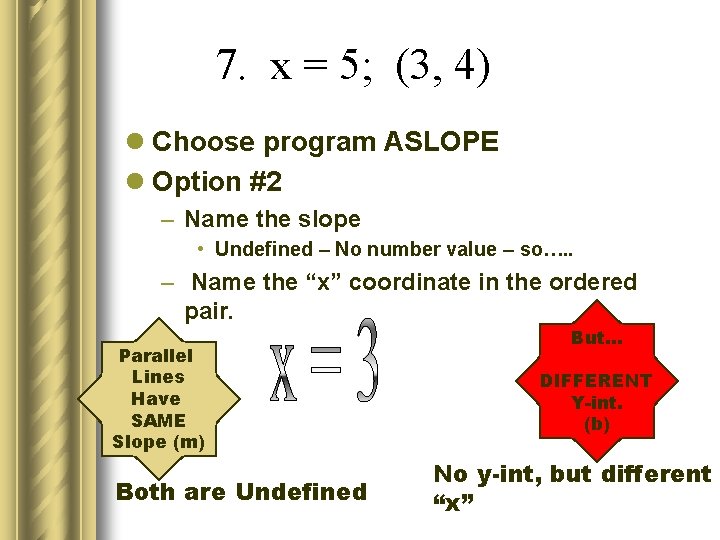
7. x = 5; (3, 4) l Choose program ASLOPE l Option #2 – Name the slope • Undefined – No number value – so…. . – Name the “x” coordinate in the ordered pair. Parallel Lines Have SAME Slope (m) Both are Undefined But… DIFFERENT Y-int. (b) No y-int, but different “x”

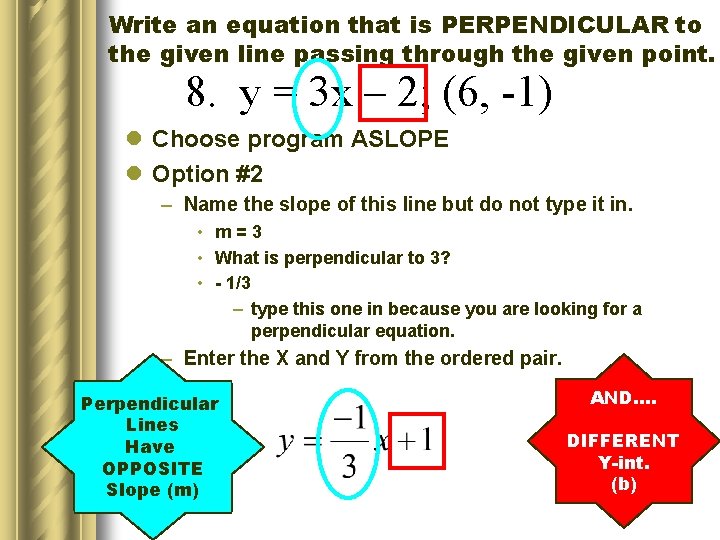
Write an equation that is PERPENDICULAR to the given line passing through the given point. 8. y = 3 x – 2; (6, -1) l Choose program ASLOPE l Option #2 – Name the slope of this line but do not type it in. • m=3 • What is perpendicular to 3? • - 1/3 – type this one in because you are looking for a perpendicular equation. – Enter the X and Y from the ordered pair. Perpendicular Lines Have OPPOSITE Slope (m) AND…. DIFFERENT Y-int. (b)

Write an equation that is PERPENDICULAR to the given line passing through the given point. Example 9 9. To get the Slope, solve For “y” • Find the PRGM key on your calculator. • Select program ASLOPE • Which option? • #2 because you have a point and a slope. Perpendicular Lines • Enter NEW (perpendicular) slope Have • Enter X and Y from your ordered pair OPPOSITE Slopes (m) AND…. DIFFERENT Y-int. (b)

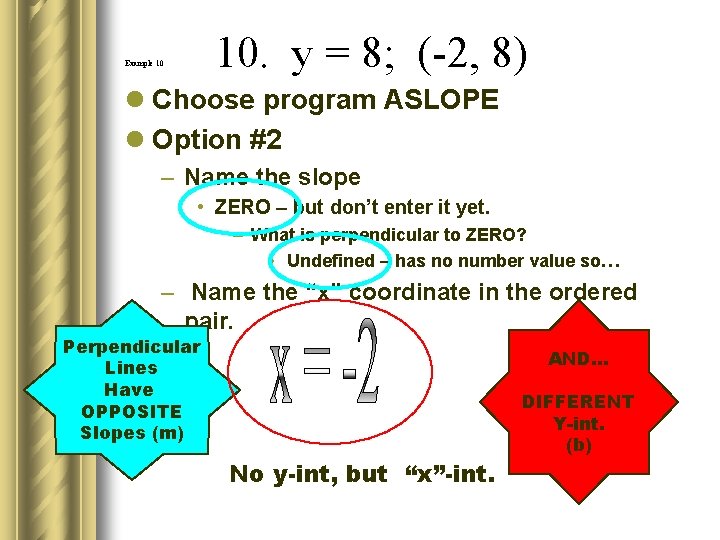
10. y = 8; (-2, 8) Example 10 l Choose program ASLOPE l Option #2 – Name the slope • ZERO – but don’t enter it yet. – What is perpendicular to ZERO? • Undefined – has no number value so… – Name the “x” coordinate in the ordered pair. Perpendicular Lines Have OPPOSITE Slopes (m) AND… No y-int, but “x”-int. DIFFERENT Y-int. (b)