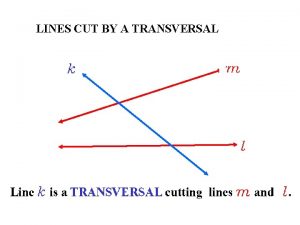
CHAPTER 3 3 3 PROVING LINES PARALLEL SAT

















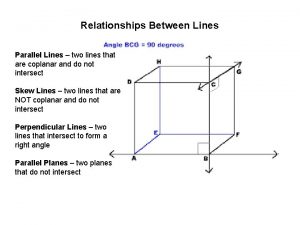
- Slides: 25

CHAPTER 3 3 -3 PROVING LINES PARALLEL

SAT PROBLEM OF THE DAY •

OBJECTIVES • Use the angles formed by a transversal to prove two lines are parallel.

CONVERSE • Recall that the converse of a theorem is found by exchanging the hypothesis and conclusion. The converse of a theorem is not automatically true. If it is true, it must be stated as a postulate or proved as a separate theorem.

CONVERSE

EXAMPLE#1 • Use the Converse of the Corresponding Angles Postulate and the given information to show that ℓ || m. 4 8 4 and 8 are corresponding angles. ℓ || m Conv. of Corr. s Post.

EXAMPLE#2 • Use the Converse of the Corresponding Angles Postulate and the given information to show that ℓ || m. m 3 = (4 x – 80)°, m 7 = (3 x – 50)°, x = 30 m 3 = 4(30) – 80 = 40 for x. Substitute 30 m 7 = 3(30) – 50 = 40 Substitute 30 • m 3 = m 7 Trans. Prop. for x. • 3 7 Def. of s. • ℓ || m Conv. of Corr. s of Equality

STUDENT GUIDED PRACTICE • Do problems 1 -3 in the book page 166

PROVING LINES PARALLEL The Converse of the Corresponding Angles Postulate is used to construct parallel lines. The Parallel Postulate guarantees that for any line ℓ, you can always construct a parallel line through a point that is not on ℓ.

THEOREMS

EXAMPLE • Use the given information and theorems you have learned to show that r || s. 4 8 4 and 8 are alternate exterior angles. r || s Conv. Of Alt. Ext. s Thm.

EXAMPLE • Use the given information and theorems you have learned to show that r || s. m 2 = (10 x + 8)°, m 3 = (25 x – 3)°, x = 5 m 2 = 10 x + 8 = 10(5) + 8 = 58 Substitute 5 for x. • m 3 = 25 x – 3 • = 25(5) – 3 = 122 Substitute 5 for x.

CONTINUE EXAMPLE • m 2 + m 3 = 58° + 122° • = 180° 2 and 3 are same-side interior angles. • r || s Conv. of Same-Side Int. s Thm.

STUDENT GUIDED PRACTICE • Do problems 4 -6 in your book page 166

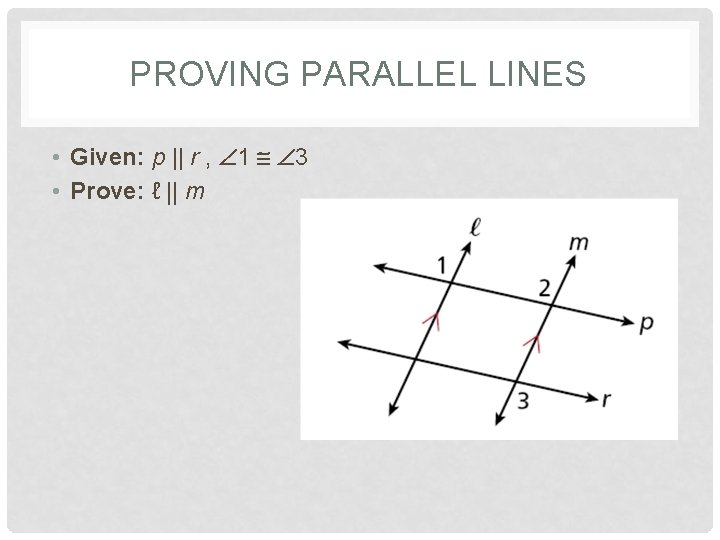
PROVING PARALLEL LINES • Given: p || r , 1 3 • Prove: ℓ || m

SOLUTION • statements 1. p || r reasons 1. Given 2. 3 2 2. Alt. Ext. s Thm. 3. 1 3 3. Given 4. 1 2 5. ℓ ||m 4. Trans. Prop. of 5. Conv. of Corr. s Post.

EXAMPLE • Given: 1 4, 3 and 4 are supplementary. • Prove: ℓ || m

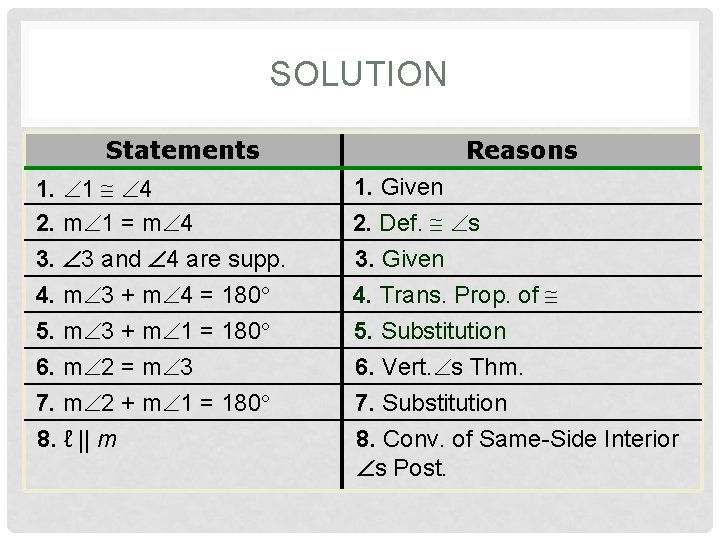
SOLUTION Statements 1. 1 4 2. m 1 = m 4 3. 3 and 4 are supp. 4. m 3 + m 4 = 180 5. m 3 + m 1 = 180 6. m 2 = m 3 7. m 2 + m 1 = 180 8. ℓ || m Reasons 1. Given 2. Def. s 3. Given 4. Trans. Prop. of 5. Substitution 6. Vert. s Thm. 7. Substitution 8. Conv. of Same-Side Interior s Post.

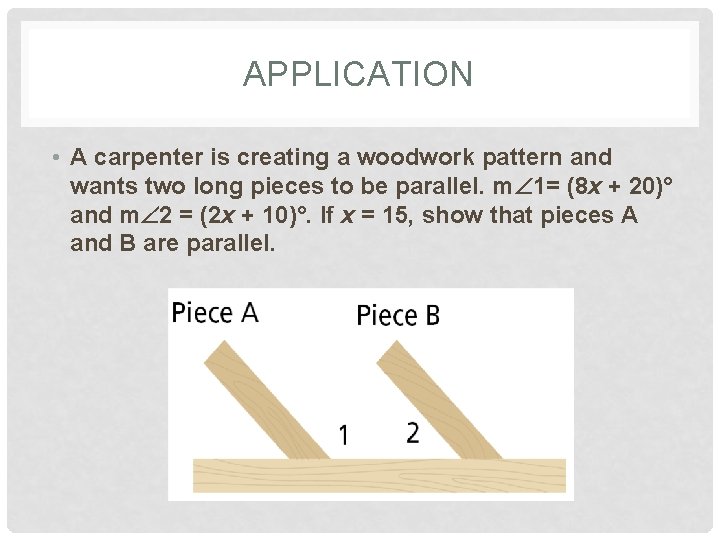
APPLICATION • A carpenter is creating a woodwork pattern and wants two long pieces to be parallel. m 1= (8 x + 20)° and m 2 = (2 x + 10)°. If x = 15, show that pieces A and B are parallel.

• A line through the center of the horizontal piece forms a transversal to pieces A and B. • 1 and 2 are same-side interior angles. If 1 and 2 are supplementary, then pieces A and B are parallel. • Substitute 15 for x in each expression.

• • m 1 = 8 x + 20 = 8(15) + 20 = 140 m 2 = 2 x + 10 = 2(15) + 10 = 40 m 1+m 2 = 140 + 40 = 180 The same-side interior angles are supplementary, so pieces A and B are parallel by the Converse of the Same -Side Interior Angles Theorem.

APPLICATION • What if…? Suppose the corresponding angles on the opposite side of the boat measure (4 y – 2)° and (3 y + 6)°, where • y = 8. Show that the oars are parallel.

CONTINUE • 4 y – 2 = 4(8) – 2 = 30° 3 y + 6 = 3(8) + 6 = 30° • The angles are congruent, so the oars are || by the Conv. of the Corr. s Post.

HOMEWORK!!! • Do problems 12 -18 and problem 22 in your book page 166 and 167

CLOSURE • Today we learned about parallel lines • Next class we are going to learned about perpendicular lines
 Geometry proving lines parallel
Geometry proving lines parallel Proving lines parallel assignment
Proving lines parallel assignment Corresponding angles flow proof
Corresponding angles flow proof Proving lines parallel with algebra
Proving lines parallel with algebra 3-3 proving lines parallel part 1 answers
3-3 proving lines parallel part 1 answers Lesson 3-5 proving lines parallel answers
Lesson 3-5 proving lines parallel answers Proving lines are parallel worksheet answers 14-3
Proving lines are parallel worksheet answers 14-3 3-3 proving lines parallel
3-3 proving lines parallel 3-5 proving lines parallel answers
3-5 proving lines parallel answers Transversal guided notes
Transversal guided notes 7-2 proving lines are parallel
7-2 proving lines are parallel Lesson 3-5 proving lines parallel
Lesson 3-5 proving lines parallel 3-5 proving lines parallel
3-5 proving lines parallel Proving lines parallel worksheet 3-3
Proving lines parallel worksheet 3-3 Lesson 4-3 proving lines are parallel
Lesson 4-3 proving lines are parallel 3-3 proving parallel lines
3-3 proving parallel lines Focal points n fingerprint pattern
Focal points n fingerprint pattern Define parallel lines and intersecting lines
Define parallel lines and intersecting lines Chapter 3 parallel and perpendicular lines
Chapter 3 parallel and perpendicular lines Chapter 3 parallel and perpendicular lines
Chapter 3 parallel and perpendicular lines Chapter 3 quiz geometry answers
Chapter 3 quiz geometry answers Chapter 3-2 angles and parallel lines
Chapter 3-2 angles and parallel lines Geometry chapter 3 review parallel and perpendicular lines
Geometry chapter 3 review parallel and perpendicular lines Chapter 2 parallel lines
Chapter 2 parallel lines Unit 4 congruent triangles homework 3
Unit 4 congruent triangles homework 3 How to find the resultant of two parallel forces
How to find the resultant of two parallel forces