Part 1 Coinciding Lines Parallel Lines Coinciding Lines

Part 1: Coinciding Lines Parallel Lines

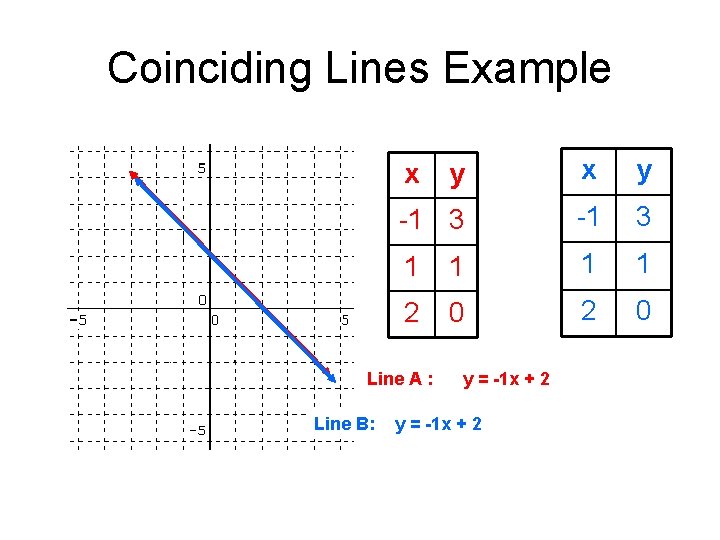
Coinciding Lines: • Definition: Lines that have all solutions in common in an input/output table. • They overlap • Same slope, same y-intercept, same line…

Coinciding Lines Example y x y -1 3 1 1 2 0 x Line A : Line B: y = -1 x + 2

Practice: Identifying Coinciding Lines Match the coinciding lines: y = 3 x + 2 -4 x + 6 y = 18 y = -1 x – 2 2 y = 6 x + 4 y = -x + 4 -5 x – 5 y = -20 y= -y = 1 x + 2 x+3

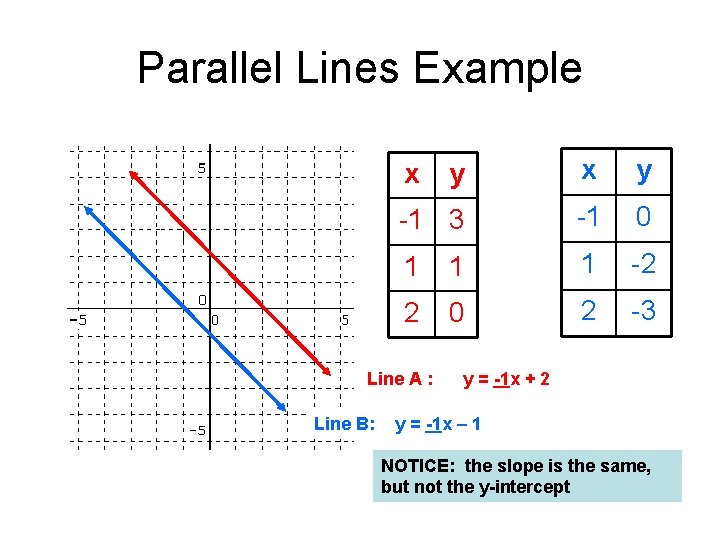
Parallel Lines: • Definition: Lines that have no intersection • No solutions the same in an input/output table • same slope, different y-intercept (same line that crosses at a different point on the y-axis)

Parallel Lines Example y x y -1 3 -1 0 1 1 1 -2 2 0 2 -3 x Line A : Line B: y = -1 x + 2 y = -1 x – 1 NOTICE: the slope is the same, but not the y-intercept

Practice: Identifying Parallel Lines Match the parallel lines: y = 3 x + 2 y= y = -1 x – 2 y=x+4 y = 3 x – 7 y= y = -x x+3 x+5

Practice: Writing Parallel Lines Write an equation of a line that is parallel to each of the following lines. y = 4 x + 2 y = 3 x – 2 y = -x + 4 y= x+3

Part 2: Perpendicular Lines Intersecting Lines

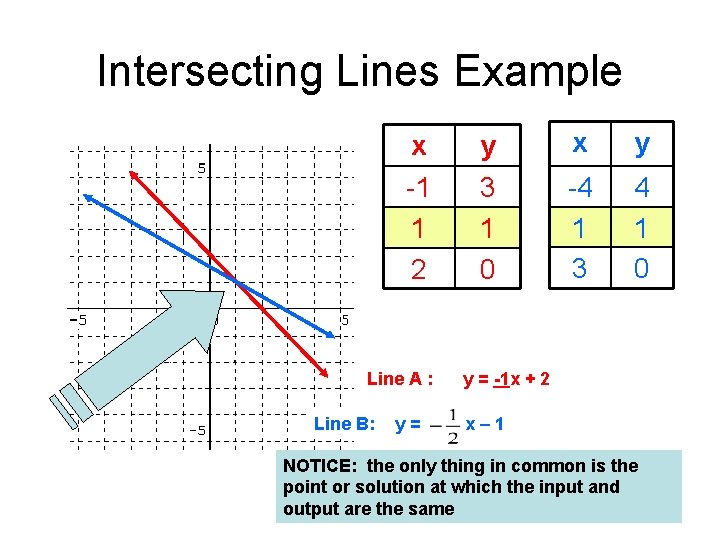
Intersecting Lines: • Definition: Lines that intersect or cross at one point • Only one solution in common- at intersection • Only one solution in common on an input/output table

Intersecting Lines Example x -1 1 2 Line A : Line B: y= y 3 1 0 x y -4 1 3 4 1 0 y = -1 x + 2 x– 1 NOTICE: the only thing in common is the point or solution at which the input and output are the same

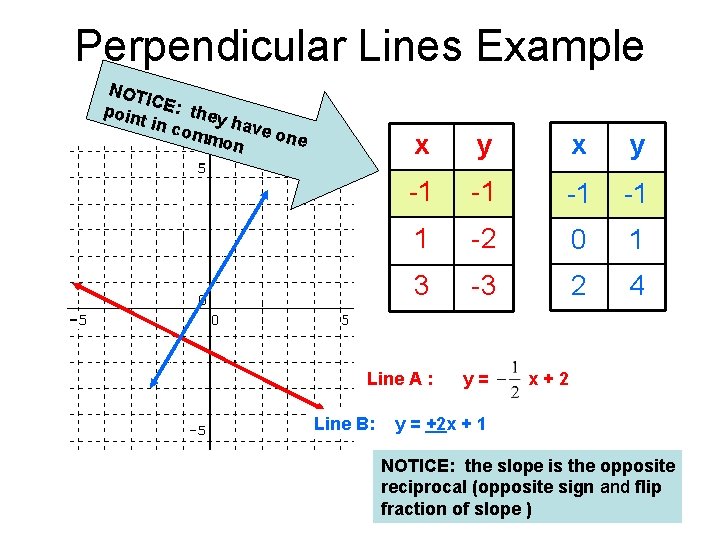
Perpendicular Lines: • Definition: Lines that intersect at one point, creating four 90 degree angles. • Only one solution in common- at intersection • Opposite reciprocal slopes of each other • Y-intercepts different *SPECIAL CASE: y-intercepts CAN be the same if they cross (intersect) on the yaxis

Perpendicular Lines Example NOT IC poin E: they t in c omm have on x y -1 -1 1 -2 0 1 3 -3 2 4 Line A : Line B: y= x+2 y = +2 x + 1 NOTICE: the slope is the opposite reciprocal (opposite sign and flip fraction of slope )

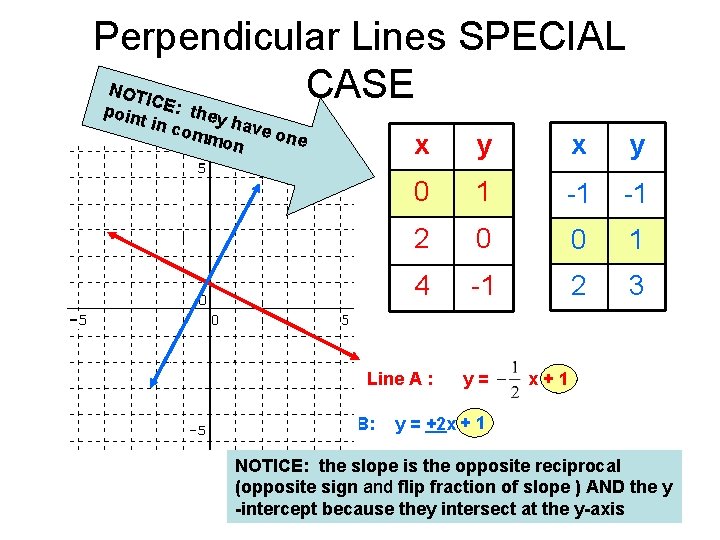
Perpendicular Lines SPECIAL NOT CASE ICE: p t oint h in co ey have mmo one n x y 0 1 -1 -1 2 0 0 1 4 -1 2 3 Line A : Line B: y= x+1 y = +2 x + 1 NOTICE: the slope is the opposite reciprocal (opposite sign and flip fraction of slope ) AND the y -intercept because they intersect at the y-axis

How to Identify Perpendicular Lines: • Slopes will have the opposite sign and reciprocal Example: y = 3 x + 1 slope is 3 or A line PERPENDICULAR will have a slope of the opposite sign and reciprocal slope will be

Practice: Identifying Perpendicular Slopes Write a slope that is perpendicular to the slope in the equations given. y = 4 x + 2 y = 3 x – 2 y = -x + 4 y= x+3

What about the Special Case? The only time that the y-intercepts match in perpendicular lines is when they intersect on the y-axis.