Proving Lines Parallel Proving Lines Parallel Postulates Theorems

Proving Lines Parallel - Postulates & Theorems • If two lines are cut by

Proving Lines Parallel - Postulates &Theorems • If two lines are cut by a

Example 3: Proving Lines Parallel • Find the value of x which will make

Theorem 4. 2 • In a plane, if 2 lines are perpendicular to the

Ways to Prove Two Lines Parallel • Show that corresponding angles are equal. •

Ex: Based on the info in the diagram, is p q ? If so,

Example 5: SAILING If two boats sail at a 45 angle to the wind

Solution: Because corresponding angles are congruent, the boats’ paths are parallel. Parallel lines do

Example 6: Identifying parallel lines Decide which rays are parallel. H E 62 A

Example: Identifying parallel lines Decide which rays are parallel. H E 58 B G

Example: Identifying parallel lines Decide which rays are parallel. H E 120 A G

Slides: 16

Download presentation

Proving Lines Parallel

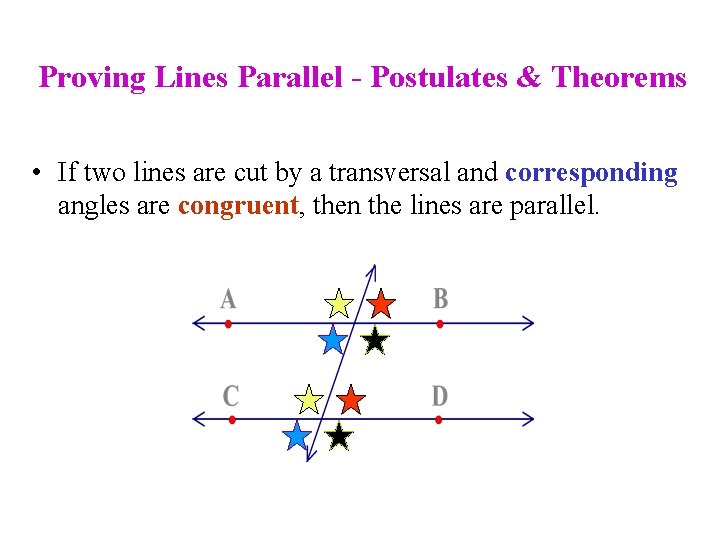
Proving Lines Parallel - Postulates & Theorems • If two lines are cut by a transversal and corresponding angles are congruent, then the lines are parallel.

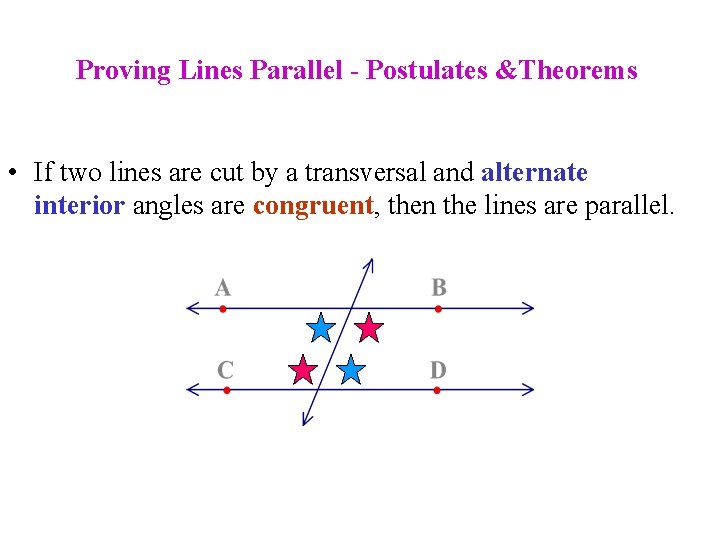
Proving Lines Parallel - Postulates &Theorems • If two lines are cut by a transversal and alternate interior angles are congruent, then the lines are parallel.

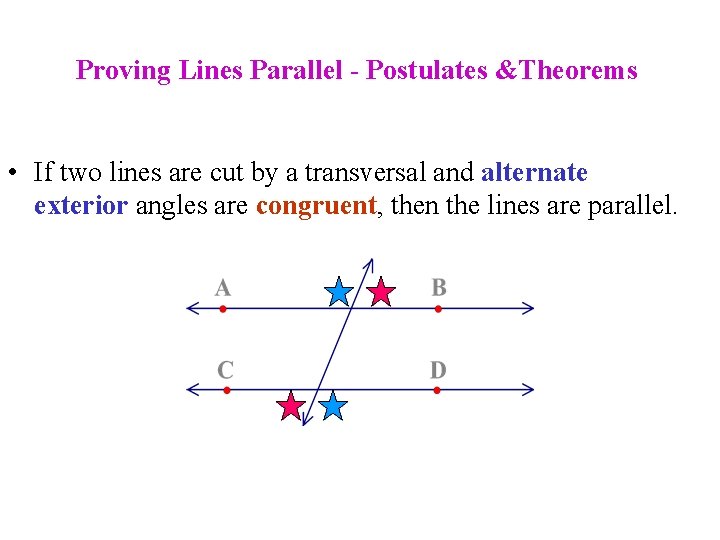
Proving Lines Parallel - Postulates &Theorems • If two lines are cut by a transversal and alternate exterior angles are congruent, then the lines are parallel.

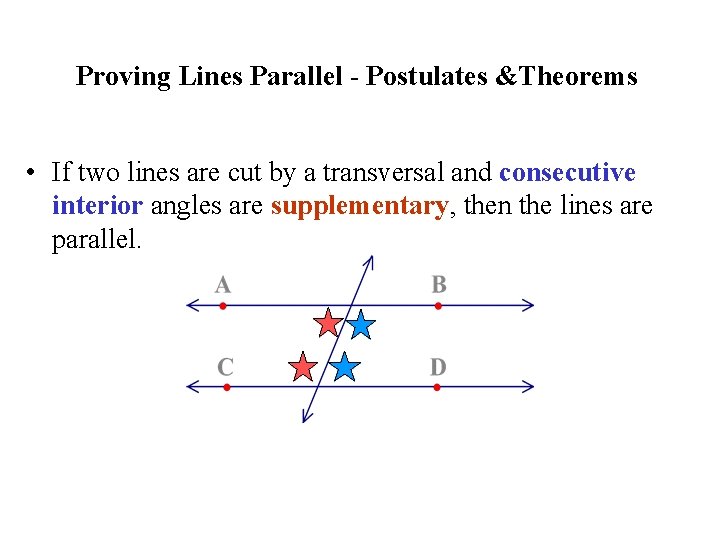
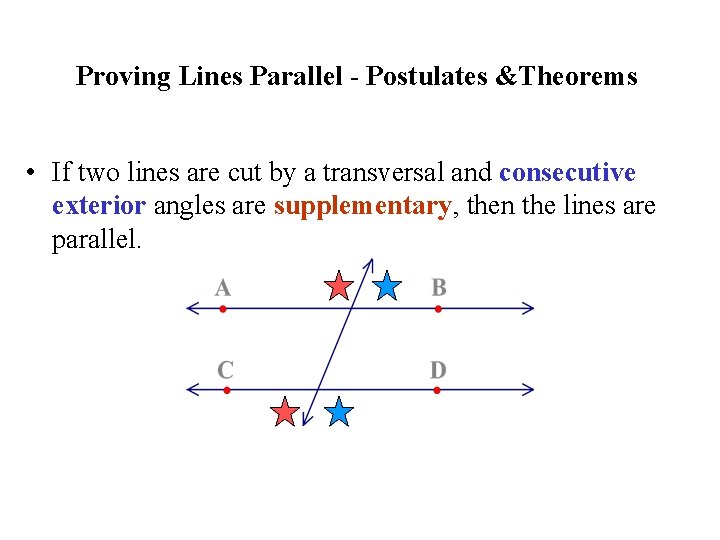
Proving Lines Parallel - Postulates &Theorems • If two lines are cut by a transversal and consecutive interior angles are supplementary, then the lines are parallel.

Proving Lines Parallel - Postulates &Theorems • If two lines are cut by a transversal and consecutive exterior angles are supplementary, then the lines are parallel.

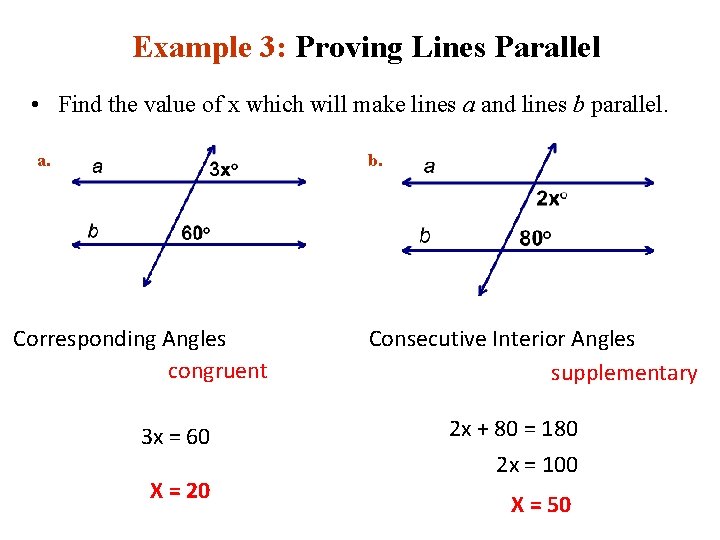
Example 3: Proving Lines Parallel • Find the value of x which will make lines a and lines b parallel. b. a. Corresponding Angles congruent 3 x = 60 X = 20 Consecutive Interior Angles supplementary 2 x + 80 = 180 2 x = 100 X = 50

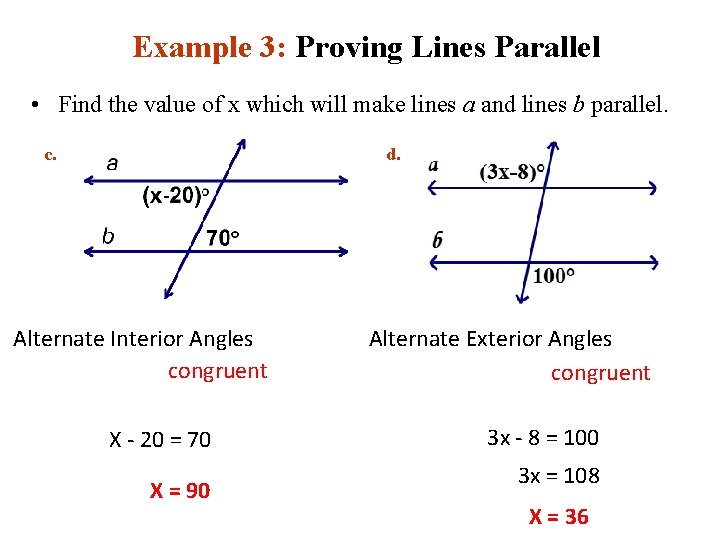
Example 3: Proving Lines Parallel • Find the value of x which will make lines a and lines b parallel. c. d. Alternate Interior Angles congruent X - 20 = 70 X = 90 Alternate Exterior Angles congruent 3 x - 8 = 100 3 x = 108 X = 36

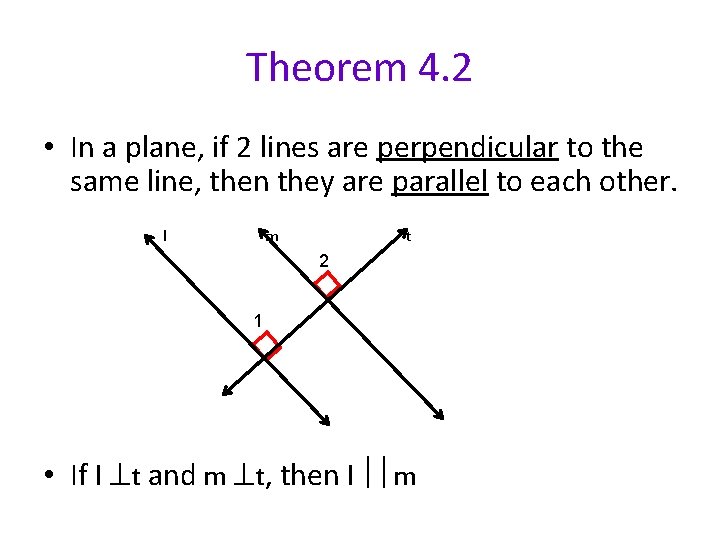
Theorem 4. 2 • In a plane, if 2 lines are perpendicular to the same line, then they are parallel to each other. l m t 2 1 • If l t and m t, then l m

Ways to Prove Two Lines Parallel • Show that corresponding angles are equal. • Show that alternative interior or alternate exterior angles are equal. • Show that consecutive interior or consecutive exterior angles are supplementary. • In a plane, show that the lines are perpendicular to the same line.

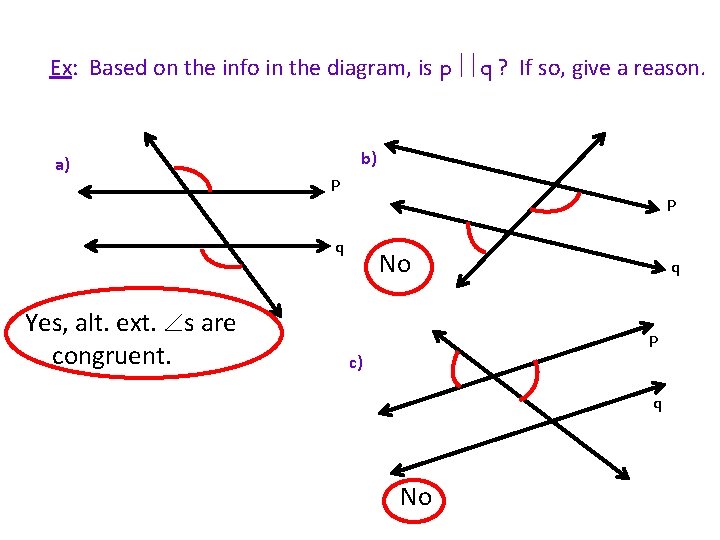
Ex: Based on the info in the diagram, is p q ? If so, give a reason. a) b) p p q Yes, alt. ext. s are congruent. No q p c) q No

Example 5: SAILING If two boats sail at a 45 angle to the wind as shown, and the wind is constant, will their paths ever cross? Explain.

Solution: Because corresponding angles are congruent, the boats’ paths are parallel. Parallel lines do not intersect, so the boats’ paths will not cross.

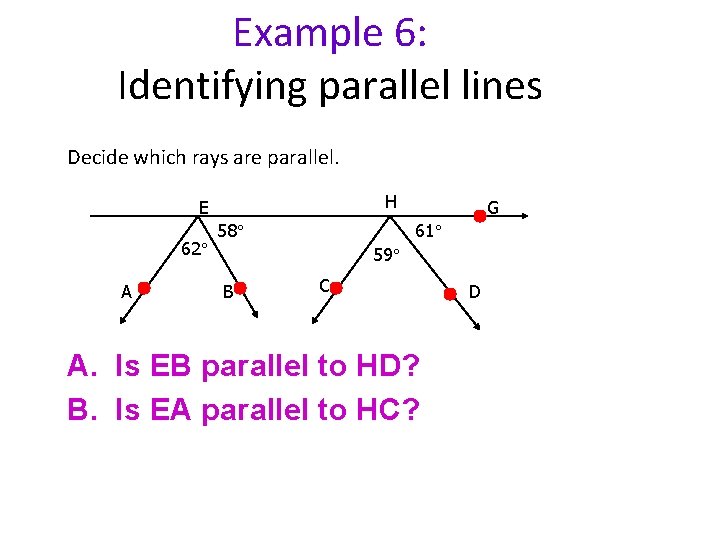
Example 6: Identifying parallel lines Decide which rays are parallel. H E 62 A 58 G 61 59 B C A. Is EB parallel to HD? B. Is EA parallel to HC? D

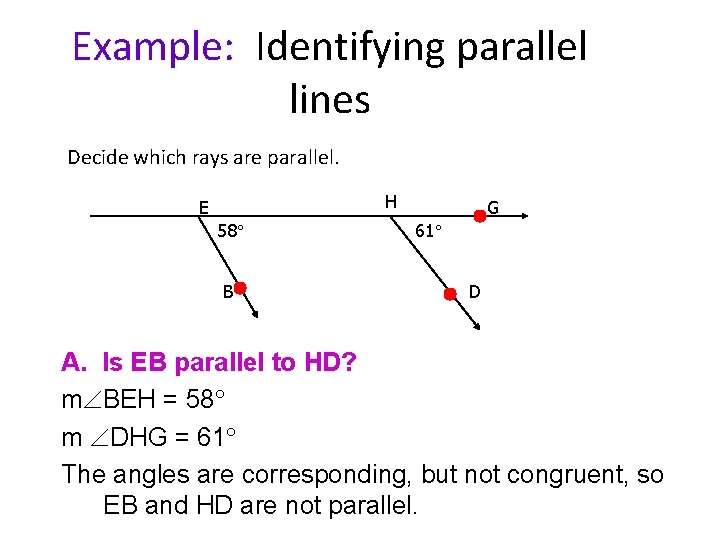
Example: Identifying parallel lines Decide which rays are parallel. H E 58 B G 61 D A. Is EB parallel to HD? m BEH = 58 m DHG = 61 The angles are corresponding, but not congruent, so EB and HD are not parallel.

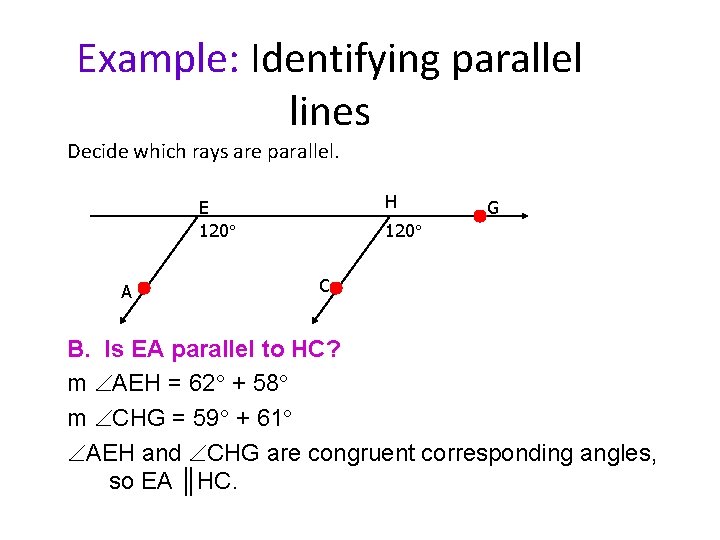
Example: Identifying parallel lines Decide which rays are parallel. H E 120 A G 120 C B. Is EA parallel to HC? m AEH = 62 + 58 m CHG = 59 + 61 AEH and CHG are congruent corresponding angles, so EA ║HC.