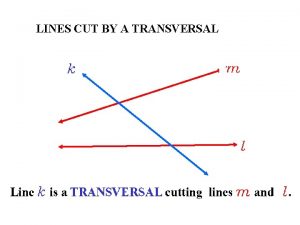
Proving Lines Parallel Holt Mc Dougal Geometry Proving

Proving Lines Parallel Holt Mc. Dougal Geometry

Proving Lines Parallel Example 1 A: Using the Converse of the Corresponding Angles Postulate Use the Converse of the Corresponding Angles Postulate and the given information to show that ℓ || m. 4 8 ℓ || m Holt Mc. Dougal Geometry 4 and 8 are corresponding angles. Conv. of Corr. s Post.

Proving Lines Parallel Example 1 B: Using the Converse of the Corresponding Angles Postulate Use the Converse of the Corresponding Angles Postulate and the given information to show that ℓ || m. m 3 = (4 x – 80)°, m 7 = (3 x – 50)°, x = 30 m 3 = 4(30) – 80 = 40 m 8 = 3(30) – 50 = 40 m 3 = m 8 3 8 ℓ || m Holt Mc. Dougal Geometry Substitute 30 for x. Trans. Prop. of Equality Def. of s. Conv. of Corr. s Post.

Proving Lines Parallel Check It Out! Example 1 a Use the Converse of the Corresponding Angles Postulate and the given information to show that ℓ || m. m 1 = m 3 1 3 ℓ || m Holt Mc. Dougal Geometry 1 and 3 are corresponding angles. Conv. of Corr. s Post.

Proving Lines Parallel Check It Out! Example 1 b Use the Converse of the Corresponding Angles Postulate and the given information to show that ℓ || m. m 7 = (4 x + 25)°, m 5 = (5 x + 12)°, x = 13 m 7 = 4(13) + 25 = 77 m 5 = 5(13) + 12 = 77 m 7 = m 5 7 5 ℓ || m Holt Mc. Dougal Geometry Substitute 13 for x. Trans. Prop. of Equality Def. of s. Conv. of Corr. s Post.

Proving Lines Parallel The Converse of the Corresponding Angles Postulate is used to construct parallel lines. The Parallel Postulate guarantees that for any line ℓ, you can always construct a parallel line through a point that is not on ℓ. Holt Mc. Dougal Geometry

Proving Lines Parallel Holt Mc. Dougal Geometry

Proving Lines Parallel Example 2 A: Determining Whether Lines are Parallel Use the given information and theorems you have learned to show that r || s. 4 8 4 and 8 are alternate exterior angles. r || s Conv. Of Alt. Int. s Thm. Holt Mc. Dougal Geometry

Proving Lines Parallel Example 2 B: Determining Whether Lines are Parallel Use the given information and theorems you have learned to show that r || s. m 2 = (10 x + 8)°, m 3 = (25 x – 3)°, x = 5 m 2 = 10 x + 8 = 10(5) + 8 = 58 Substitute 5 for x. m 3 = 25 x – 3 = 25(5) – 3 = 122 Substitute 5 for x. Holt Mc. Dougal Geometry

Proving Lines Parallel Example 2 B Continued Use the given information and theorems you have learned to show that r || s. m 2 = (10 x + 8)°, m 3 = (25 x – 3)°, x = 5 m 2 + m 3 = 58° + 122° = 180° r || s Holt Mc. Dougal Geometry 2 and 3 are same-side interior angles. Conv. of Same-Side Int. s Thm.

Proving Lines Parallel Check It Out! Example 2 a Refer to the diagram. Use the given information and theorems you have learned to show that r || s. m 4 = m 8 4 8 Congruent angles 4 8 4 and 8 are alternate exterior angles. r || s Conv. of Alt. Int. s Thm. Holt Mc. Dougal Geometry

Proving Lines Parallel Check It Out! Example 2 b Refer to the diagram. Use the given information and theorems you have learned to show that r || s. m 3 = 2 x , m 7 = (x + 50) , x = 50 m 3 = 2 x = 2(50) = 100° Substitute 50 for x. m 7 = x + 50 = 50 + 50 = 100° Substitute 5 for x. m 3 = 100 and m 7 = 100 3 7 r||s Conv. of the Alt. Int. s Thm. Holt Mc. Dougal Geometry

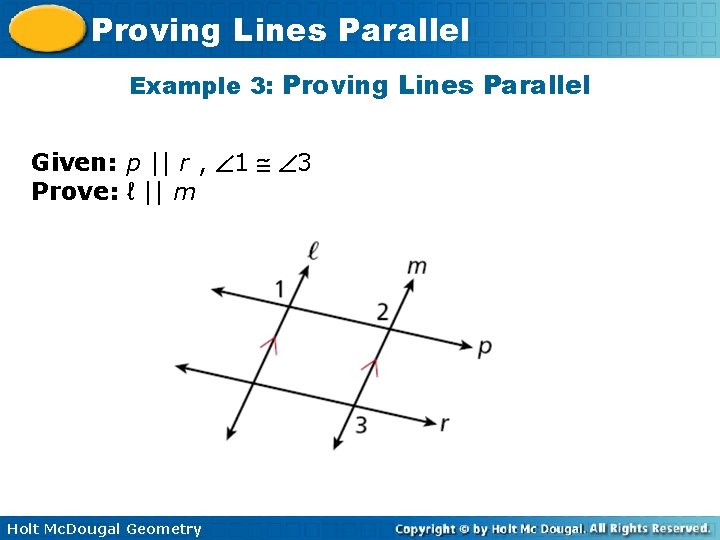
Proving Lines Parallel Example 3: Proving Lines Parallel Given: p || r , 1 3 Prove: ℓ || m Holt Mc. Dougal Geometry

Proving Lines Parallel Example 3 Continued Statements Reasons 1. p || r 1. Given 2. 3 2 2. Alt. Ext. s Thm. 3. 1 3 3. Given 4. 1 2 4. Trans. Prop. of 5. ℓ ||m 5. Conv. of Corr. s Post. Holt Mc. Dougal Geometry

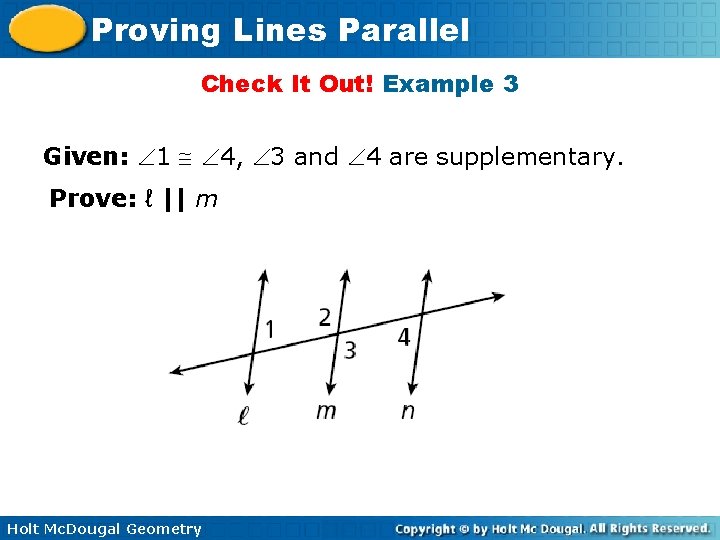
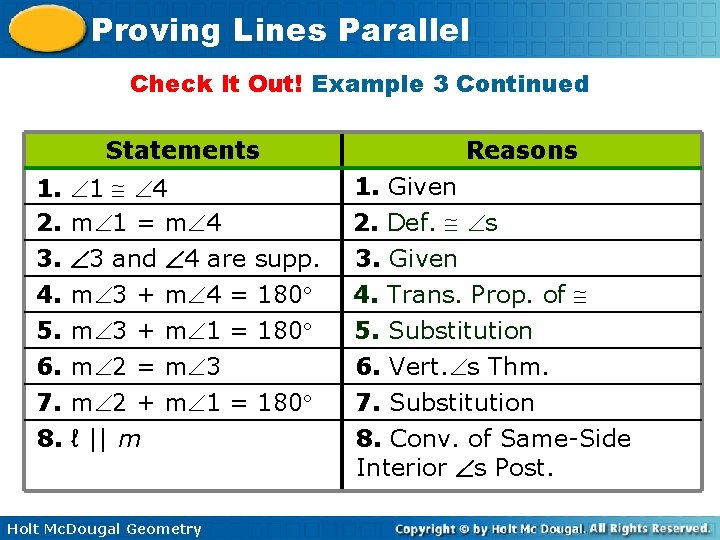
Proving Lines Parallel Check It Out! Example 3 Given: 1 4, 3 and 4 are supplementary. Prove: ℓ || m Holt Mc. Dougal Geometry

Proving Lines Parallel Check It Out! Example 3 Continued Statements Reasons 1. 1 4 2. m 1 = m 4 1. Given 2. Def. s 3. 4. 5. 6. 7. 3. Given 4. Trans. Prop. of 3 and 4 are supp. m 3 + m 4 = 180 m 3 + m 1 = 180 m 2 = m 3 m 2 + m 1 = 180 8. ℓ || m Holt Mc. Dougal Geometry 5. Substitution 6. Vert. s Thm. 7. Substitution 8. Conv. of Same-Side Interior s Post.

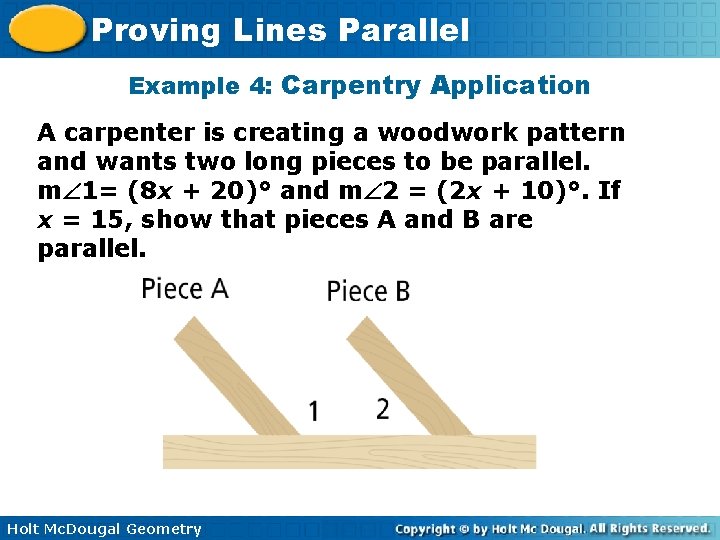
Proving Lines Parallel Example 4: Carpentry Application A carpenter is creating a woodwork pattern and wants two long pieces to be parallel. m 1= (8 x + 20)° and m 2 = (2 x + 10)°. If x = 15, show that pieces A and B are parallel. Holt Mc. Dougal Geometry

Proving Lines Parallel Example 4 Continued A line through the center of the horizontal piece forms a transversal to pieces A and B. 1 and 2 are same-side interior angles. If 1 and 2 are supplementary, then pieces A and B are parallel. Substitute 15 for x in each expression. Holt Mc. Dougal Geometry

Proving Lines Parallel Example 4 Continued m 1 = 8 x + 20 = 8(15) + 20 = 140 Substitute 15 for x. m 2 = 2 x + 10 = 2(15) + 10 = 40 m 1+m 2 = 140 + 40 = 180 Substitute 15 for x. 1 and 2 are supplementary. The same-side interior angles are supplementary, so pieces A and B are parallel by the Converse of the Same-Side Interior Angles Theorem. Holt Mc. Dougal Geometry

Proving Lines Parallel Check It Out! Example 4 What if…? Suppose the corresponding angles on the opposite side of the boat measure (4 y – 2)° and (3 y + 6)°, where y = 8. Show that the oars are parallel. 4 y – 2 = 4(8) – 2 = 30° 3 y + 6 = 3(8) + 6 = 30° The angles are congruent, so the oars are || by the Conv. of the Corr. s Post. Holt Mc. Dougal Geometry

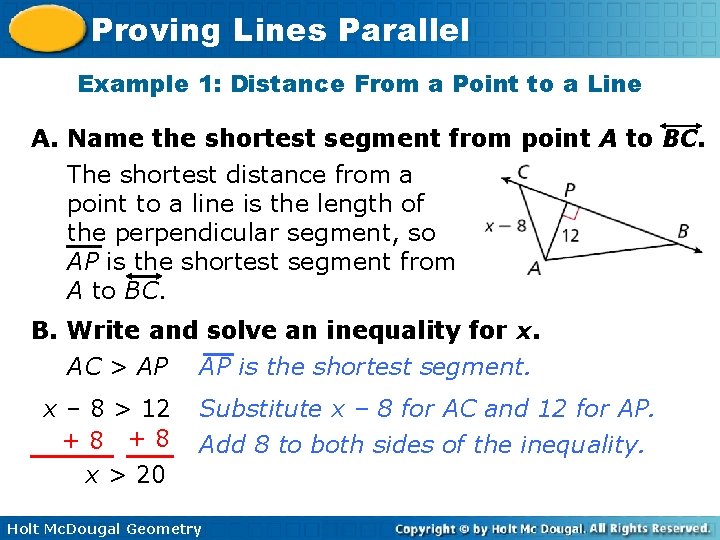
Proving Lines Parallel Example 1: Distance From a Point to a Line A. Name the shortest segment from point A to BC. The shortest distance from a point to a line is the length of the perpendicular segment, so AP is the shortest segment from A to BC. B. Write and solve an inequality for x. AC > AP AP is the shortest segment. x – 8 > 12 +8 +8 x > 20 Substitute x – 8 for AC and 12 for AP. Add 8 to both sides of the inequality. Holt Mc. Dougal Geometry

Proving Lines Parallel Check It Out! Example 1 A. Name the shortest segment from point A to BC. The shortest distance from a point to a line is the length of the perpendicular segment, so AB is the shortest segment from A to BC. B. Write and solve an inequality for x. AB is the shortest segment. AC > AB 12 > x – 5 Substitute 12 for AC and x – 5 for AB. +5 + 5 Add 5 to both sides of the inequality. 17 > x Holt Mc. Dougal Geometry

Proving Lines Parallel HYPOTHESIS CONCLUSION Holt Mc. Dougal Geometry

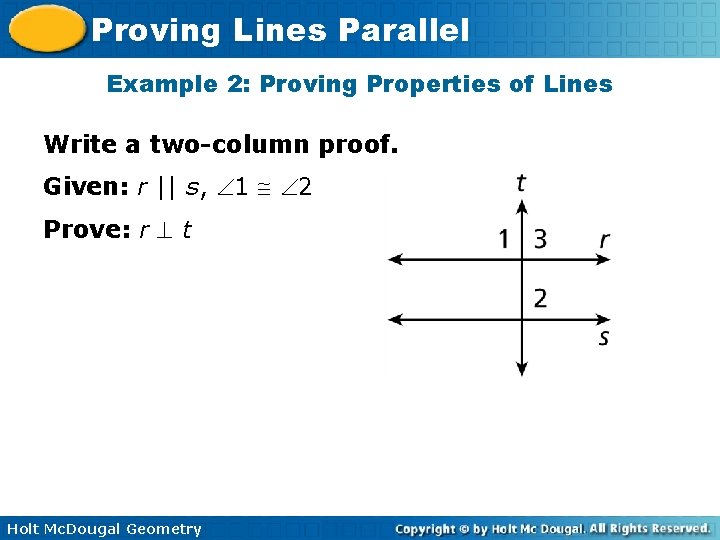
Proving Lines Parallel Example 2: Proving Properties of Lines Write a two-column proof. Given: r || s, 1 2 Prove: r t Holt Mc. Dougal Geometry

Proving Lines Parallel Example 2 Continued Statements Reasons 1. r || s, 1 2 1. Given 2. 2 3 2. Corr. s Post. 3. 1 3 3. Trans. Prop. of 4. r t 4. 2 intersecting lines form lin. pair of s lines . Holt Mc. Dougal Geometry

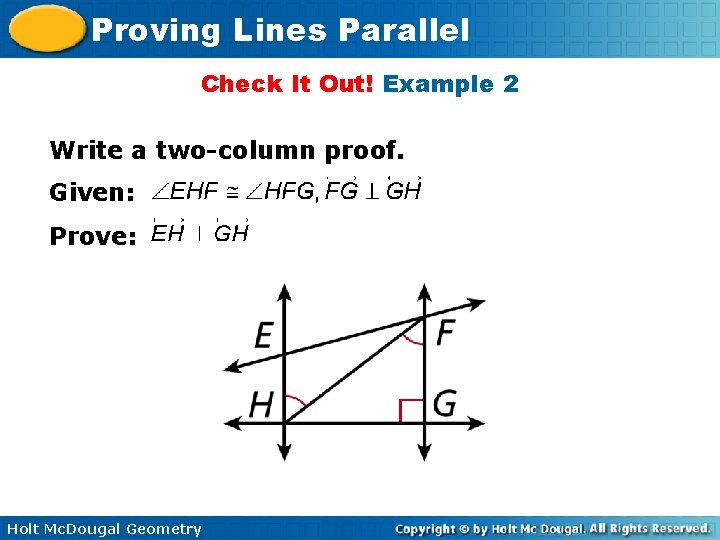
Proving Lines Parallel Check It Out! Example 2 Write a two-column proof. Given: Prove: Holt Mc. Dougal Geometry

Proving Lines Parallel Check It Out! Example 2 Continued Statements Reasons 1. EHF HFG 1. Given 2. Conv. of Alt. Int. s Thm. 3. Given 4. Transv. Thm. Holt Mc. Dougal Geometry

Proving Lines Parallel Example 3: Carpentry Application A carpenter’s square forms a right angle. A carpenter places the square so that one side is parallel to an edge of a board, and then draws a line along the other side of the square. Then he slides the square to the right and draws a second line. Why must the two lines be parallel? Both lines are perpendicular to the edge of the board. If two coplanar lines are perpendicular to the same line, then the two lines are parallel to each other, so the lines must be parallel to each other. Holt Mc. Dougal Geometry

Proving Lines Parallel Check It Out! Example 3 A swimmer who gets caught in a rip current should swim in a direction perpendicular to the current. Why should the path of the swimmer be parallel to the shoreline? Holt Mc. Dougal Geometry

Proving Lines Parallel Check It Out! Example 3 Continued The shoreline and the path of the swimmer should both be to the current, so they should be || to each other. Holt Mc. Dougal Geometry