3 1 Parallel Lines and Transversals Chapter 3

3. 1: Parallel Lines and Transversals Chapter 3: Angles and Triangles S

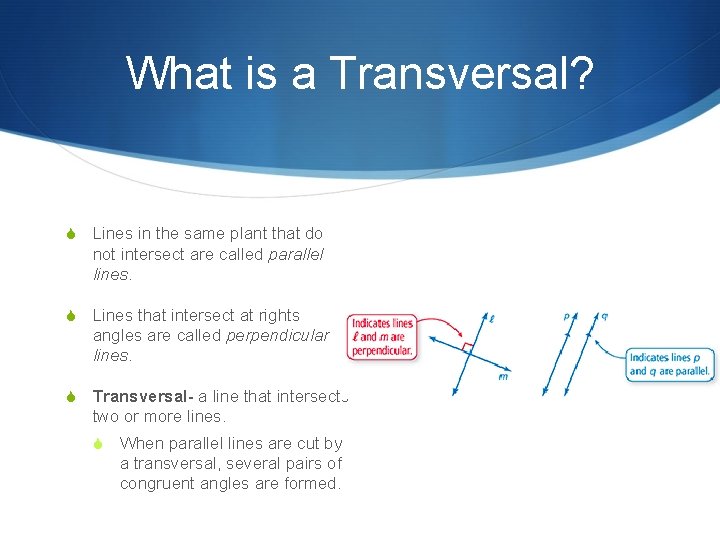
What is a Transversal? S Lines in the same plant that do not intersect are called parallel lines. S Lines that intersect at rights angles are called perpendicular lines. S Transversal- a line that intersects two or more lines. S When parallel lines are cut by a transversal, several pairs of congruent angles are formed.

Corresponding Angles S When a transversal intersects parallel lines, corresponding angles are congruent.

Finding Angle Measures Use the figure to find the measures of (a) <1 and (b) <2. S (a) <1 and the 110 degree angles are corresponding angles. They are congruent S So, the measure of <1 is 110 S <1 and <2 are supplementary, The sum of the angles is 180 degrees.

Practice Use the figure to find the measure of <1 and <2. explain your reasoning. S <1 and 63 degrees are corresponding angles, sot <1 is 63 degrees. S <1 and <2 are supplementary angles.

Using Corresponding Angles Use the figure to find the measures of the numbered angles. S <1 and the 75 degree angle are vertical angles, so they are congruent. S So, <1=75 S The 75 degree angle is supplementary to both <2 and <3. S So, the measures of <2 and <3 are 105 Using corresponding angles, the measures of <4 and<6 are 75, and the measures of <5 and <7 are 105.

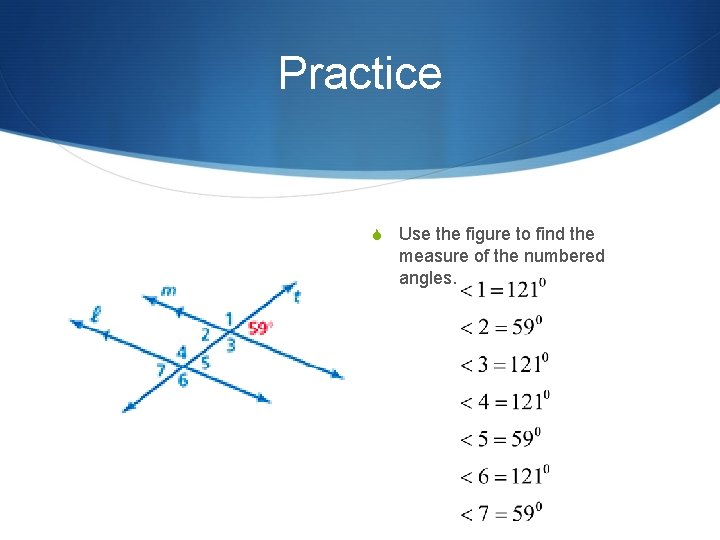
Practice S Use the figure to find the measure of the numbered angles.

Interior and Exterior Angles S When two parallel lines are cut by a transversal: S Four interior angles are formed on the inside of the parallel lines. S Four exterior angles are formed on the outside of the parallel lines. S <3, <4, <5, and <6 are interior angles. S <1, <2, <7, and <8 are exterior angles.

Using Corresponding Angles S A store owner uses pieces of tape to paint a window advertisement. The letters are slanted at an 80 degree angle. What is the measure of <1? S Because all the letters are slanted at an 80 degree angle, the dashed lines are parallel. The pieces of tape is the transversal. S Using corresponding angles, the 80 degree angle is congruent to the angle that is supplementary to <1. The measure of <1 is 180 -80=100 degrees.

Alternate Interior and Alternate Exterior Angles S When a transversal intersects parallel lines S Alternate interior angles are congruent S Alternate exterior angles are congruent

Identifying Alternate Interior and Alternate Exterior Angles The photo shows a portion of an airport. Describe the relationship between each pair of angles. S <3 and <6 are alternate exterior angles. S <3 is congruent to <6 S <2 and <7 are alternate interior angles. S <2 is congruent to <7