Angles and Parallel Lines Intersecting Lines Lines that

Angles and Parallel Lines

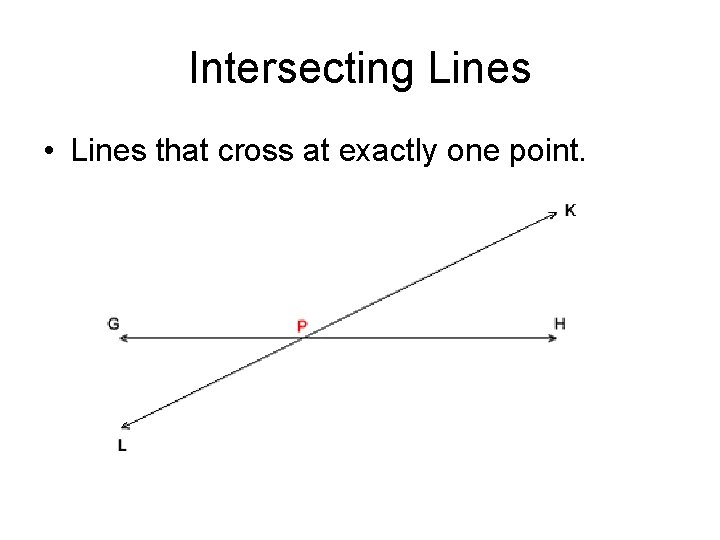
Intersecting Lines • Lines that cross at exactly one point.

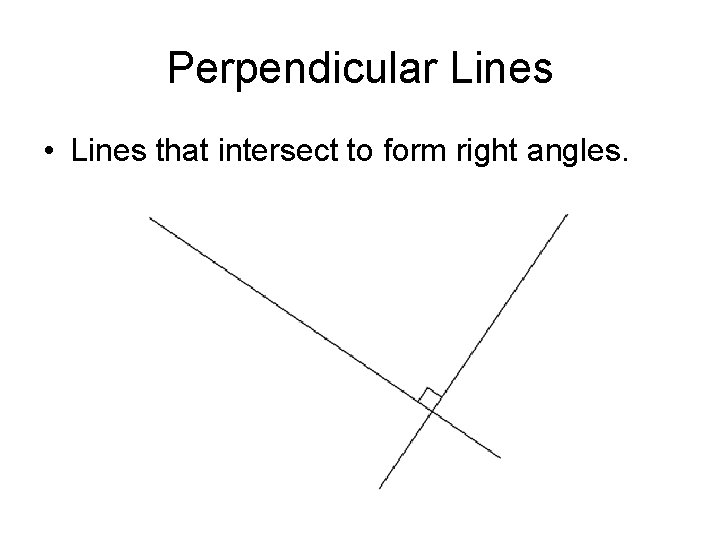
Perpendicular Lines • Lines that intersect to form right angles.

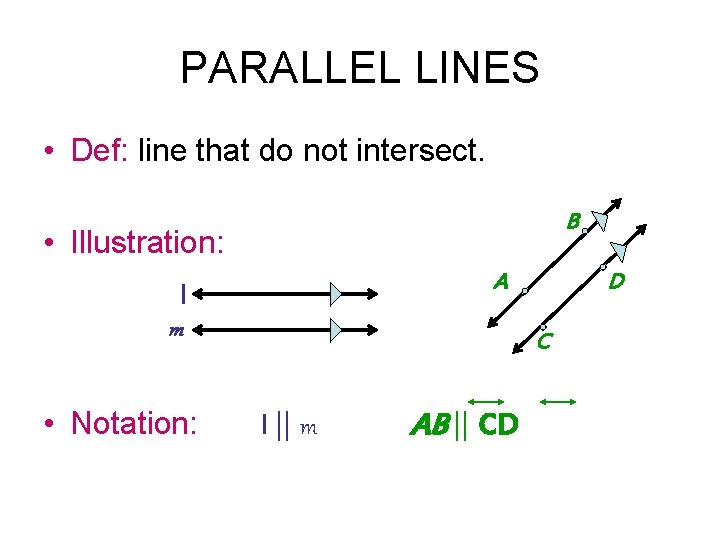
PARALLEL LINES • Def: line that do not intersect. B • Illustration: A l m • Notation: D C l || m AB || CD

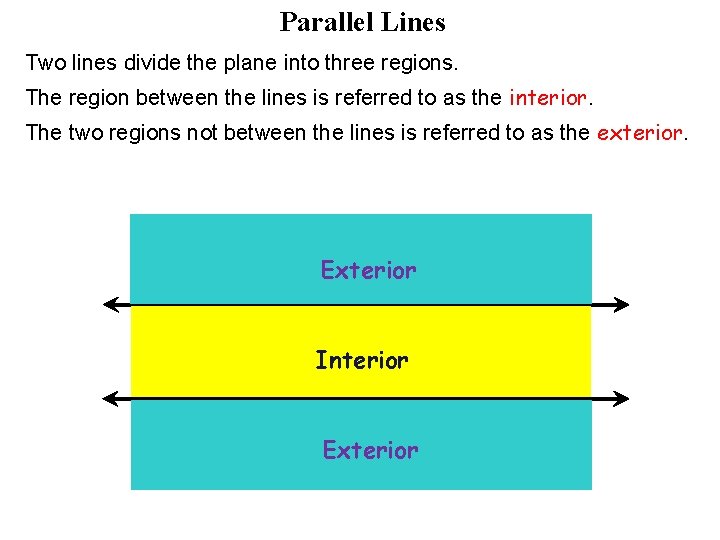
Parallel Lines Two lines divide the plane into three regions. The region between the lines is referred to as the interior. The two regions not between the lines is referred to as the exterior. Exterior Interior Exterior

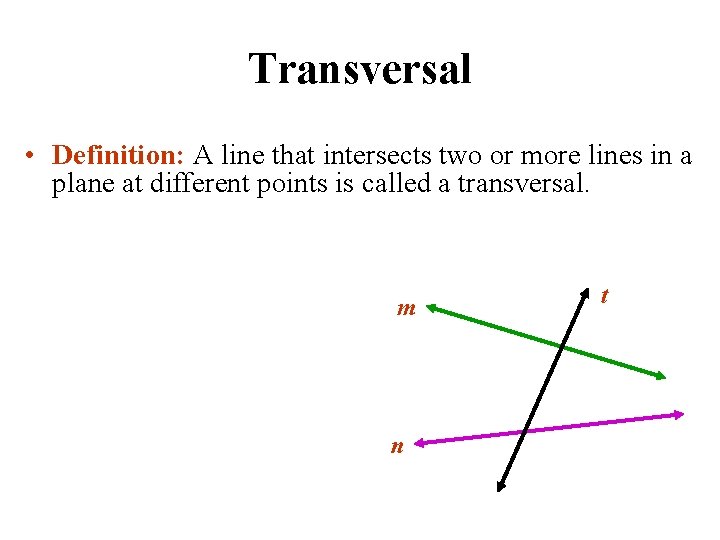
Transversal • Definition: A line that intersects two or more lines in a plane at different points is called a transversal. m n t

Vertical Angles & Linear Pair Vertical Angles: Two angles that are opposite angles. Vertical angles are congruent. 1 4, 2 3, 5 8, 6 7 Linear Pair: Supplementary angles that form a line (sum = 180 ) 1 & 2 , 2 & 4 , 4 & 3, 3 & 1, 5 & 6, 6 & 8, 8 & 7, 7 & 5 1 3 4 5 7 6 8 2

Supplementary Angles/ Linear Pair • Two angles that form a line (sum=180 ) 1+ 2=180 2+ 4=180 4+ 3=180 3+ 1=180 t 1 2 3 4 5 7 6 8 5+ 6=180 6+ 8=180 8+ 7=180 7+ 5=180

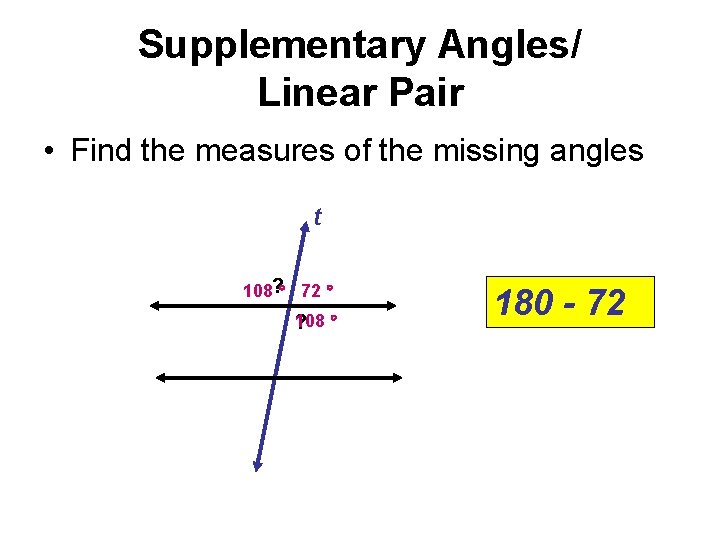
Supplementary Angles/ Linear Pair • Find the measures of the missing angles t 108? 72 108 ? 180 - 72

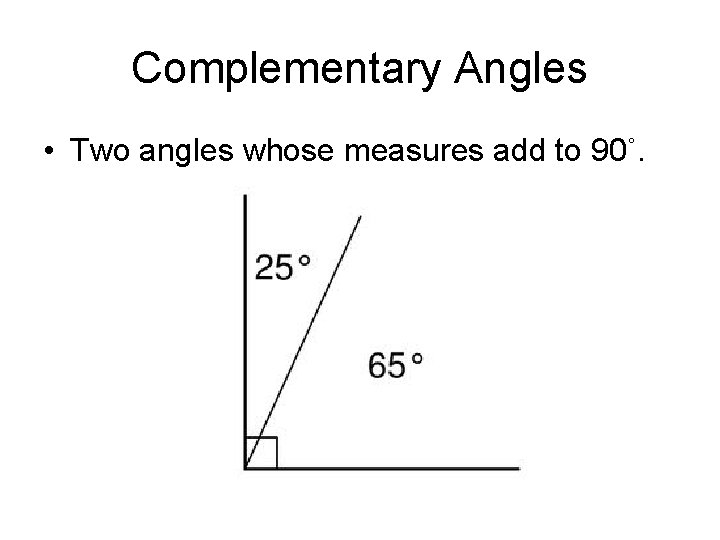
Complementary Angles • Two angles whose measures add to 90˚.

Adjacent Angles • Angles in the same plane that have a common vertex and a common side.

Angles and Parallel Lines • 1. 2. 3. • 1. 2. If two parallel lines are cut by a transversal, then the following pairs of angles are congruent. Corresponding angles Alternate interior angles Alternate exterior angles If two parallel lines are cut by a transversal, then the following pairs of angles are supplementary. Consecutive interior angles Continued…. . Consecutive exterior angles

Corresponding Angles: Two angles that occupy corresponding positions. 2 6, 1 5, 3 7, 4 8 1 3 4 5 7 2 6 8

Consecutive Angles Consecutive Interior Angles: Two angles that lie between parallel lines on the same sides of the transversal. m 3 +m 5 = 180º, m 4 +m 6 = 180º Consecutive Exterior Angles: Two angles that lie outside parallel lines on the same sides of the transversal. 1 2 m 1 +m 7 = 180º, m 2 +m 8 = 180º 3 4 5 6 7 8

Alternate Angles • Alternate Interior Angles: Two angles that lie between parallel lines on opposite sides of the transversal (but not a 3 6, 4 5 linear pair). • Alternate Exterior Angles: Two angles that lie outside parallel lines on opposite sides of the transversal. 1 3 4 5 7 2 6 8 2 7, 1 8

Example: If line AB is parallel to line CD and s is parallel to t, find the measure of all the angles when m< 1 = 100°. Justify your answers. A 1 4 C 5 8 m<2=80° m<3=100° m<4=80° 2 12 3 6 13 14 16 15 7 s m<5=100° m<6=80° m<7=100° m<8=80° m<9=100° m<10=80° m<11=100° m<12=80° m<13=100° m<14=80° m<15=100° m<16=80° 9 t 10 11 B D

Example: If line AB is parallel to line CD and s is parallel to t, find: 1. the value of x, if m<3 = 4 x + 6 and the m<11 = 126. 2. the value of x, if m<1 = 100 and m<8 = 2 x + 10. 3. the value of y, if m<11 = 3 y – 5 and m<16 = 2 y + 20. ANSWERS: 1. 30 A 4 C 5 8 2. 35 3. 33 1 s 2 9 12 3 6 13 14 16 15 7 t 10 11 B D