Chapter 9 Estimating the Value of a Parameter

Chapter 9 Estimating the Value of a Parameter Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Section 9. 1 Estimating a Population Proportion Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objectives 1. Obtain a point estimate for the population proportion 2. Construct and interpret a confidence interval for the population proportion 3. Determine the sample size necessary for estimating the population proportion within a specified margin of error 9 -3 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objective 1 • Obtain a Point Estimate for the Population Proportion 9 -4 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

A point estimate is the value of a statistic that estimates the value of a parameter. For example, the point estimate for the population proportion is , where x is the number of individuals in the sample with a specified characteristic and n is the sample size. 9 -5 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Parallel Example 1: Calculating a Point Estimate for the Population Proportion In July of 2008, a Quinnipiac University Poll asked 1783 registered voters nationwide whether they favored or opposed the death penalty for persons convicted of murder. 1123 were in favor. Obtain a point estimate for the proportion of registered voters nationwide who are in favor of the death penalty for persons convicted of murder. 9 -6 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Solution Obtain a point estimate for the proportion of registered voters nationwide who are in favor of the death penalty for persons convicted of murder. 9 -7 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objective 2 • Construct and Interpret a Confidence Interval for the Population Proportion 9 -8 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

A confidence interval for an unknown parameter consists of an interval of numbers based on a point estimate. The level of confidence represents the expected proportion of intervals that will contain the parameter if a large number of different samples is obtained. The level of confidence is denoted (1 – α)· 100%. 9 -9 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

For example, a 95% level of confidence (α = 0. 05) implies that if 100 different confidence intervals are constructed, each based on a different sample from the same population, we will expect 95 of the intervals to contain the parameter and 5 not to include the parameter. 9 -10 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Confidence interval estimates for the population proportion are of the form Point estimate ± margin of error. The margin of error of a confidence interval estimate of a parameter is a measure of how accurate the point estimate is. 9 -11 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

The margin of error depends on three factors: Level of confidence: As the level of confidence increases, the margin of error also increases. Sample size: As the size of the random sample increases, the margin of error decreases. Standard deviation of the population: The more spread there is in the population, the wider our interval will be for a given level of confidence. 9 -12 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Sampling Distribution of For a simple random sample of size n, the sampling distribution of normal with mean is approximately and standard deviation , provided that np(1 – p) ≥ 10. NOTE: We also require that each trial be independent; when sampling from finite populations (n ≤ 0. 05 N). 9 -13 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Constructing a (1 – α)· 100% Confidence Interval for a Population Proportion Suppose that a simple random sample of size n is taken from a population. A (1 – α)· 100% confidence interval for p is given by the following quantities Lower bound: Upper bound: Note: It must be the case that n ≤ 0. 05 N to construct this interval. 9 -14 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc. and

Interpretation of a Confidence Interval A (1 – α)· 100% confidence interval indicates that (1 – α)· 100% of all simple random samples of size n from the population whose parameter is unknown will result in an interval that contains the parameter. 9 -15 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Margin of Error The margin of error, E, in a (1 – α) 100% confidence interval for a population proportion is given by 9 -16 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Parallel Example 2: Constructing a Confidence Interval for a Population Proportion In July of 2008, a Quinnipiac University Poll asked 1783 registered voters nationwide whether they favored or opposed the death penalty for persons convicted of murder. 1123 were in favor. Obtain a 90% confidence interval for the proportion of registered voters nationwide who are in favor of the death penalty for persons convicted of murder. 9 -17 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Solution • • sample size is definitely less than 5% of the population size • α = 0. 10 so zα/2 = z 0. 05 = 1. 645 • Lower bound: • Upper bound: 9 -18 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc. and the

Solution We are 90% confident that the proportion of registered voters who are in favor of the death penalty for those convicted of murder is between 0. 61 and 0. 65. 9 -19 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objective 3 • Determine the Sample Size Necessary for Estimating a Population Proportion within a Specified Margin of Error 9 -20 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

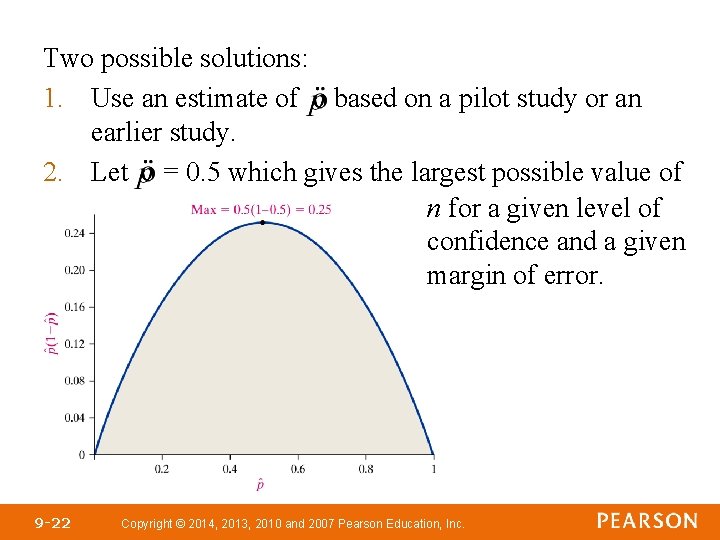
Sample size needed for a specified margin of error, E, and level of confidence (1 – α): Problem: The formula uses which depends on n, the quantity we are trying to determine! 9 -21 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Two possible solutions: 1. Use an estimate of based on a pilot study or an earlier study. 2. Let = 0. 5 which gives the largest possible value of n for a given level of confidence and a given margin of error. 9 -22 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Sample Size Needed for Estimating the Population Proportion p The sample size required to obtain a (1 – α)· 100% confidence interval for p with a margin of error E is given by (rounded up to the next integer), where estimate of p. 9 -23 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc. is a prior

Sample Size Needed for Estimating the Population Proportion p If a prior estimate of p is unavailable, the sample size required is 9 -24 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Parallel Example 4: Determining Sample Size A sociologist wanted to determine the percentage of residents of America that only speak English at home. What size sample should be obtained if she wishes her estimate to be within 3 percentage points with 90% confidence assuming she uses the 2000 estimate obtained from the Census 2000 Supplementary Survey of 82. 4%? 9 -25 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Solution • E = 0. 03 • • • We round this value up to 437. The sociologist must survey 437 randomly selected American residents. 9 -26 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Section 9. 2 Estimating a Population Mean Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objectives 1. 2. 3. 4. Obtain a point estimate for the population mean State properties of Student’s t-distribution Determine t-values Construct and interpret a confidence interval for a population mean 5. Find the sample size needed to estimate the population mean within a given margin or error 9 -28 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objective 1 • Obtain a Point Estimate for the Population Mean 9 -29 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

A point estimate is the value of a statistic that estimates the value of a parameter. For example, the sample mean, , is a point estimate of the population mean μ. 9 -30 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

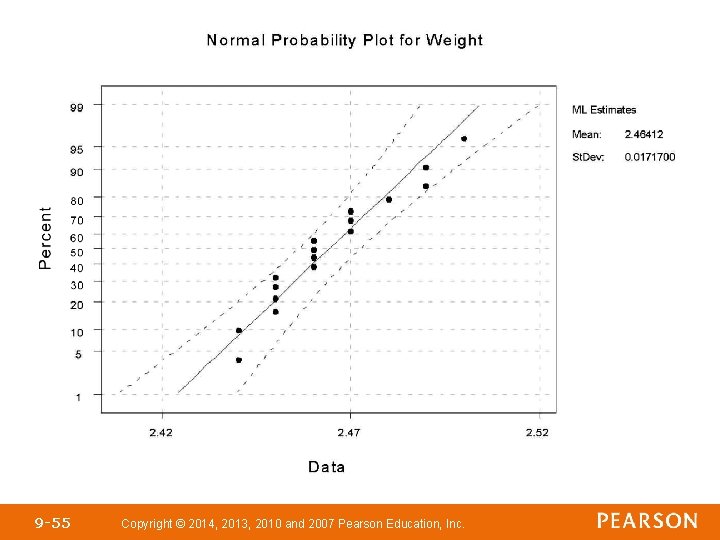
Parallel Example 1: Computing a Point Estimate Pennies minted after 1982 are made from 97. 5% zinc and 2. 5% copper. The following data represent the weights (in grams) of 17 randomly selected pennies minted after 1982. 2. 46 2. 47 2. 49 2. 48 2. 50 2. 44 2. 46 2. 45 2. 49 2. 47 2. 45 2. 46 2. 47 2. 44 2. 45 Treat the data as a simple random sample. Estimate the population mean weight of pennies minted after 1982. 9 -31 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Solution The sample mean is The point estimate of μ is 2. 464 grams. 9 -32 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objective 2 • State Properties of Student’s t-Distribution 9 -33 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Student’s t-Distribution Suppose that a simple random sample of size n is taken from a population. If the population from which the sample is drawn follows a normal distribution, the distribution of follows Student’s t-distribution with n – 1 degrees of freedom where is the sample mean and s is the sample standard deviation. (population SD is not known) 9 -34 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

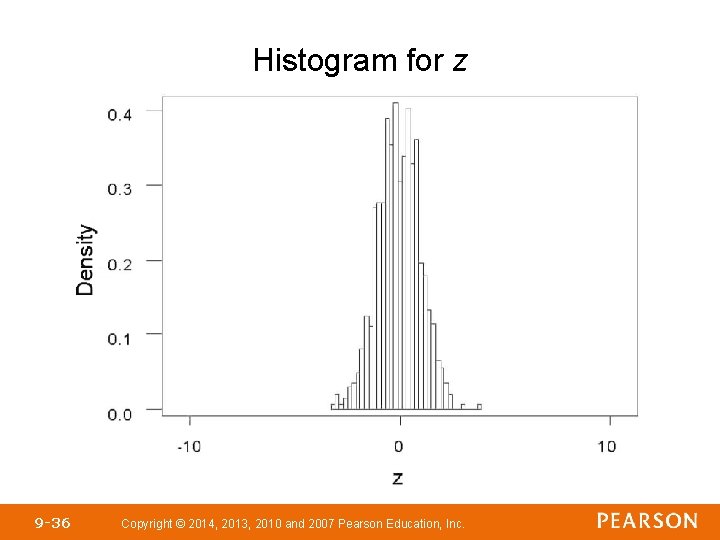
Parallel Example 1: Comparing the Standard Normal Distribution to the t-Distribution Using Simulation a) Obtain 1, 000 simple random samples of size n = 5 from a normal population with μ = 50 and σ = 10. b) Determine the sample mean and sample standard deviation for each of the samples. c) Compute and d) Draw a histogram for both z and t. 9 -35 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc. for each sample.

Histogram for z 9 -36 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

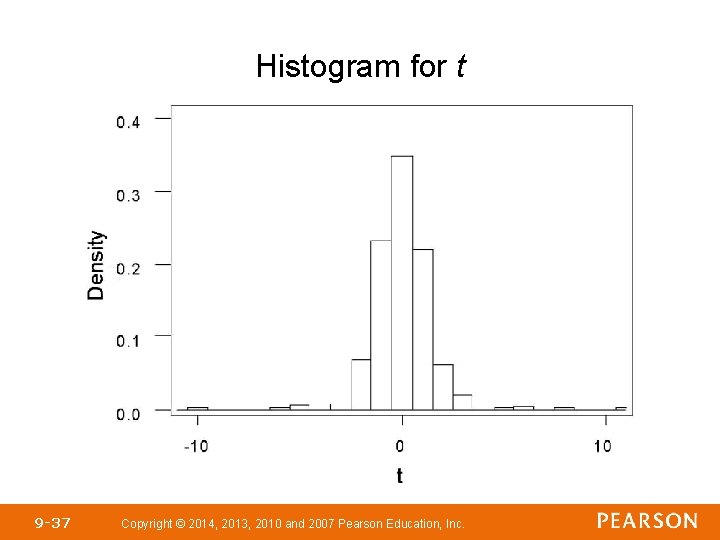
Histogram for t 9 -37 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

CONCLUSION: • The histogram for z is symmetric and bell-shaped with the center of the distribution at 0 and virtually all the rectangles between – 3 and 3. In other words, z follows a standard normal distribution. 9 -38 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

CONCLUSION (continued): • The histogram for t is also symmetric and bell-shaped with the center of the distribution at 0, but the distribution of t has longer tails (i. e. , t is more dispersed), so it is unlikely that t follows a standard normal distribution. The additional spread in the distribution of t can be attributed to the fact that we use s to find t instead of σ. Because the sample standard deviation is itself a random variable (rather than a constant such as σ), we have more dispersion in the distribution of t. 9 -39 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

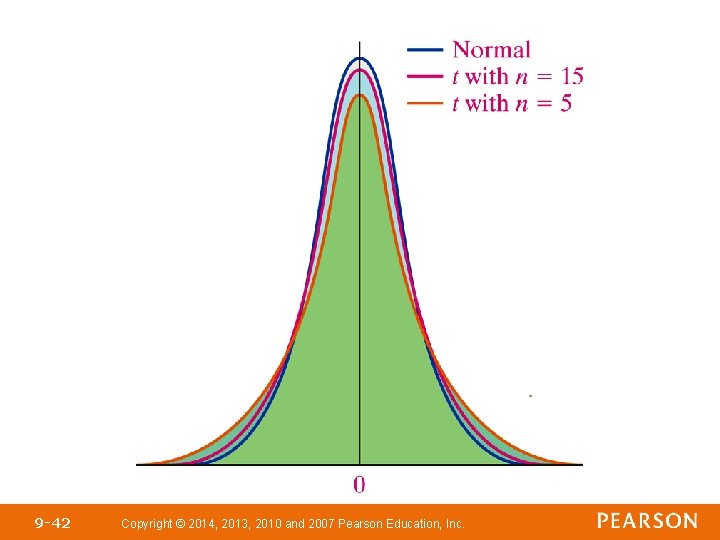
Properties of the t-Distribution 1. The t-distribution is different for different degrees of freedom. 2. The t-distribution is centered at 0 and is symmetric about 0. 3. The area under the curve is 1. The area under the curve to the right of 0 equals the area under the curve to the left of 0, which equals 1/2. 4. As t increases or decreases without bound, the graph approaches, but never equals, zero. 9 -40 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Properties of the t-Distribution 5. The area in the tails of the t-distribution is a little greater than the area in the tails of the standard normal distribution, because we are using s as an estimate of σ, thereby introducing further variability into the tstatistic. 6. As the sample size n increases, the density curve of t gets closer to the standard normal density curve. This result occurs because, as the sample size n increases, the values of s get closer to the values of σ, by the Law of Large Numbers. 9 -41 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

9 -42 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

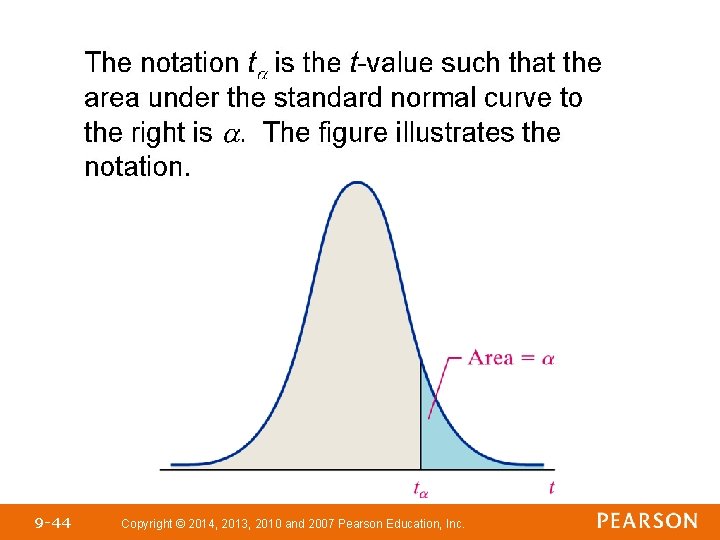
Objective 3 • Determine t-Values 9 -43 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

9 -44 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

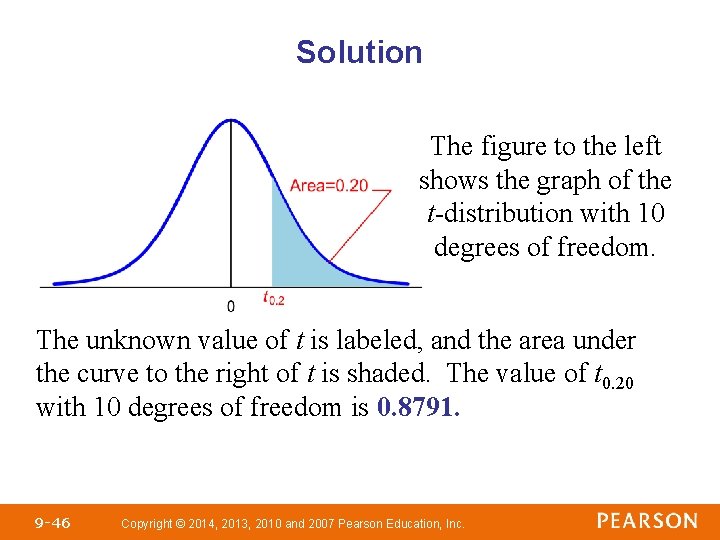
Parallel Example 2: Finding t-values Find the t-value such that the area under the t-distribution to the right of the t-value is 0. 2 assuming 10 degrees of freedom. That is, find t 0. 20 with 10 degrees of freedom. 9 -45 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Solution The figure to the left shows the graph of the t-distribution with 10 degrees of freedom. The unknown value of t is labeled, and the area under the curve to the right of t is shaded. The value of t 0. 20 with 10 degrees of freedom is 0. 8791. 9 -46 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objective 4 • Construct and Interpret a Confidence Interval for the Population Mean 9 -47 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Constructing a (1 – α)100% Confidence Interval for μ Provided • Sample data come from a simple random sample or randomized experiment • Sample size is small relative to the population size (n ≤ 0. 05 N) • The data come from a population that is normally distributed, or the sample size is large A (1 – α)· 100% confidence interval for μ is given by Lower Upper bound: where 9 -48 is the critical value with n – 1 df. Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Constructing a (1 – α)100% Confidence Interval for μ A (1 – α)· 100% confidence interval for μ is given by Lower bound: where 9 -49 Upper bound: is the critical value with n – 1 df. Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Parallel Example 2: Using Simulation to Demonstrate the Idea of a Confidence Interval We will use Minitab to simulate obtaining 30 simple random samples of size n = 8 from a population that is normally distributed with μ = 50 and σ = 10. Construct a 95% confidence interval for each sample. How many of the samples result in intervals that contain μ = 50 ? 9 -50 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

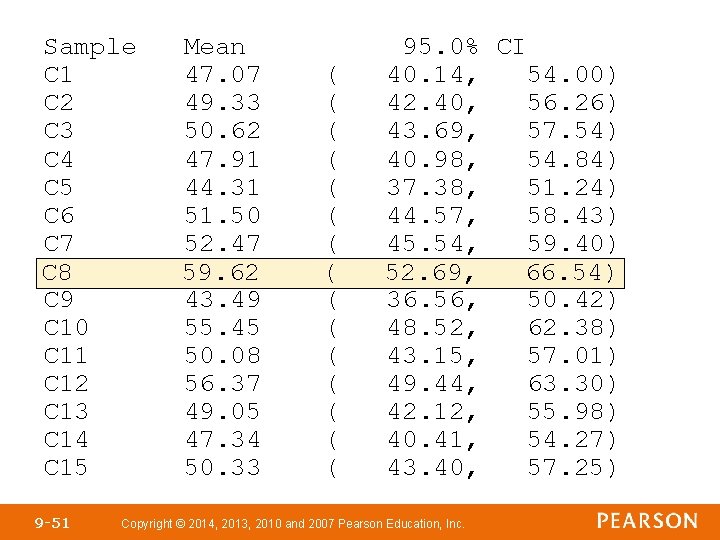
Sample C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 C 9 C 10 C 11 C 12 C 13 C 14 C 15 9 -51 Mean 47. 07 49. 33 50. 62 47. 91 44. 31 51. 50 52. 47 59. 62 43. 49 55. 45 50. 08 56. 37 49. 05 47. 34 50. 33 ( ( ( ( 95. 0% CI 40. 14, 54. 00) 42. 40, 56. 26) 43. 69, 57. 54) 40. 98, 54. 84) 37. 38, 51. 24) 44. 57, 58. 43) 45. 54, 59. 40) 52. 69, 66. 54) 36. 56, 50. 42) 48. 52, 62. 38) 43. 15, 57. 01) 49. 44, 63. 30) 42. 12, 55. 98) 40. 41, 54. 27) 43. 40, 57. 25) Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

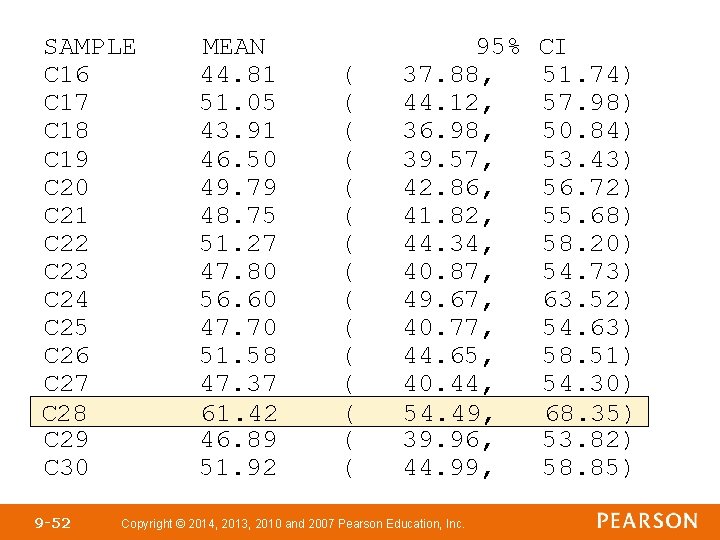
SAMPLE C 16 C 17 C 18 C 19 C 20 C 21 C 22 C 23 C 24 C 25 C 26 C 27 C 28 C 29 C 30 9 -52 MEAN 44. 81 51. 05 43. 91 46. 50 49. 79 48. 75 51. 27 47. 80 56. 60 47. 70 51. 58 47. 37 61. 42 46. 89 51. 92 ( ( ( ( 95% 37. 88, 44. 12, 36. 98, 39. 57, 42. 86, 41. 82, 44. 34, 40. 87, 49. 67, 40. 77, 44. 65, 40. 44, 54. 49, 39. 96, 44. 99, Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc. CI 51. 74) 57. 98) 50. 84) 53. 43) 56. 72) 55. 68) 58. 20) 54. 73) 63. 52) 54. 63) 58. 51) 54. 30) 68. 35) 53. 82) 58. 85)

Note that 28 out of 30, or 93%, of the confidence intervals contain the population mean μ = 50. In general, for a 95% confidence interval, any sample mean that lies within 1. 96 standard errors(area to the left is 0. 975) of the population mean will result in a confidence interval that contains μ. Whether a confidence interval contains μ depends solely on the sample mean, . 9 -53 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

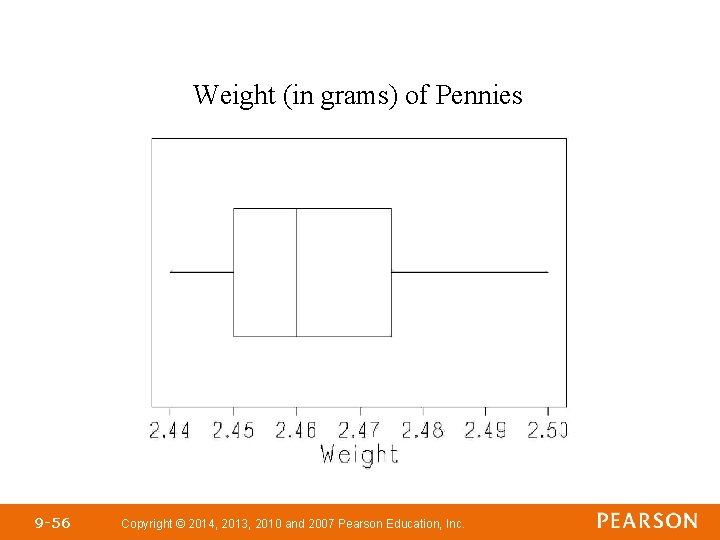
Parallel Example 3: Constructing a Confidence Interval Construct a 99% confidence interval about the population mean weight (in grams) of pennies minted after 1982. Assume μ = 0. 02 grams. 2. 46 2. 47 2. 49 2. 48 2. 50 2. 44 2. 46 2. 45 2. 49 2. 47 2. 45 2. 46 2. 47 2. 44 2. 45 9 -54 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

9 -55 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Weight (in grams) of Pennies 9 -56 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

• • Lower bound: = 2. 464 – 2. 575 = 2. 464 – 0. 012 = 2. 452 • Upper bound: = 2. 464 + 2. 575 = 2. 464 + 0. 012 = 2. 476 We are 99% confident that the mean weight of pennies minted after 1982 is between 2. 452 and 2. 476 grams. 9 -57 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Objective 5 • Find the Sample Size Needed to Estimate the Population Mean within a Given Margin of Error 9 -58 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Determining the Sample Size n The sample size required to estimate the population mean, µ, with a level of confidence (1 – α)· 100% with a specified margin of error, E, is given by where n is rounded up to the nearest whole number. 9 -59 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

Parallel Example 7: Determining the Sample Size Back to the pennies. How large a sample would be required to estimate the mean weight of a penny manufactured after 1982 within 0. 005 grams with 99% confidence? Assume = 0. 02. 9 -60 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.

• • s = 0. 02 • E = 0. 005 Rounding up, we find n = 107. 9 -61 Copyright © 2014, 2013, 2010 and 2007 Pearson Education, Inc.