Chapter 8 Estimating With Confidence Confidence Interval for









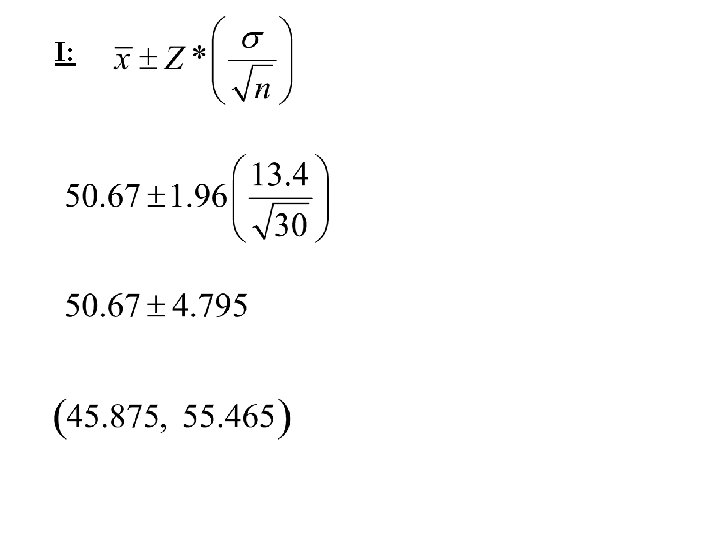




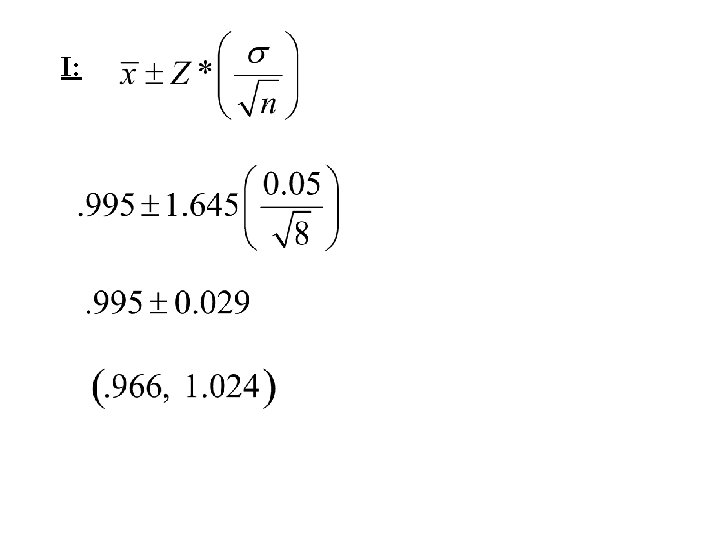





- Slides: 20

Chapter 8: Estimating With Confidence

Confidence Interval for a Population mean ( known) (Z-Interval) estimate margin of error estimate critical value standard error

Properties of Confidence Intervals • The interval is always centered around the statistic • The higher the confidence level, the wider the interval becomes • If you increase n, then the margin of error decreases

Interpreting a Confidence Interval: What you will say: I am C% confident that interval _______ to ____ captures the true parameter. What it means: If we took many, SRS from a population and calculated a confidence interval for each sample, C% of the confidence intervals will contain the true mean

CAUTION! Never Say: The interval will capture the true mean C% of the time. It either does or does not!

Conditions for a Z-Interval for a Mean: 1. SRS (should say) 2. Normality (CLT or population approx normal) 3. Independence (Population 10 x sample size)

Steps to Construct ANY Confidence Interval: PANIC P: Parameter of Interest (what are you looking for? ) A: Assumptions (what are the conditions? ) N: Name the type of interval (what type of data do we have? ) I: Interval (Finally! You can calculate!) C: Conclusion in context (I am ___% confident the true parameter lies between ____ and _____)

Example #1 Serum Cholesterol-Dr. Paul Oswick wants to estimate the true mean serum HDL cholesterol for all of his 20 -29 year old female patients. He randomly selects 30 patients and computes the sample mean to be 50. 67. Assume from past records, the population standard deviation for the serum HDL cholesterol for 20 -29 year old female patients is =13. 4. a. Construct a 95% confidence interval for the mean serum HDL cholesterol for all of Dr. Oswick’s 20 -29 year old female patients. P: The true mean serum HDL cholesterol for all of Dr. Oswick’s 20 -29 year old female patients.

A: SRS: Says randomly selected Normality: Approximately normal by the CLT (n 30) Independence: I am assuming that Dr. Oswick has 300 patients or more. N: One sample Z-Interval
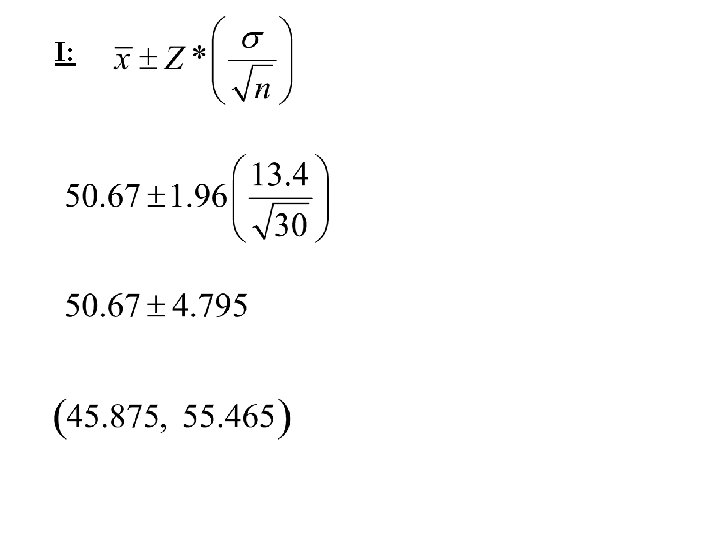
I:

C: I am 95% confident the true mean serum HDL cholesterol for all of Dr. Oswick’s 20 -29 year old female patients is between 45. 875 and 55. 465 b. If the US National Center for Health Statistics reports the mean serum HDL cholesterol for females between 20 -29 years old to be = 53, do Dr. Oswick’s patients appear to have a different serum level compared to the general population? Explain. No, 53 is contained in the interval.

Example #1 Serum Cholesterol-Dr. Paul Oswick wants to estimate the true mean serum HDL cholesterol for all of his 20 -29 year old female patients. He randomly selects 30 patients and computes the sample mean to be 50. 67. Assume from past records, the population standard deviation for the serum HDL cholesterol for 20 -29 year old female patients is =13. 4. c. What two things could you do to decrease your margin of error? Increase n Lower confidence level

Example #2 Suppose your class is investigating the weights of Snickers 1 ounce Fun-Size candy bars to see if customers are getting full value for their money. Assume that the weights are Normally distributed with standard deviation = 0. 05 ounces. Several candy bars are randomly selected and weighed with sensitive balances borrowed from the physics lab. The weights are 0. 95 1. 02 0. 98 0. 97 1. 05 1. 01 0. 98 1. 00 ounces. Determine a 90% confidence interval for the true mean, µ. Can you say that the bars weigh 1 oz on average? P: The true mean weight of Snickers 1 -oz Fun-size candy bars

A: SRS: Says randomly selected Normality: Approximately normal because the population is approximately normal Independence: I am assuming that Snickers has 80 bars or more in the 1 -oz size N: One sample Z-Interval
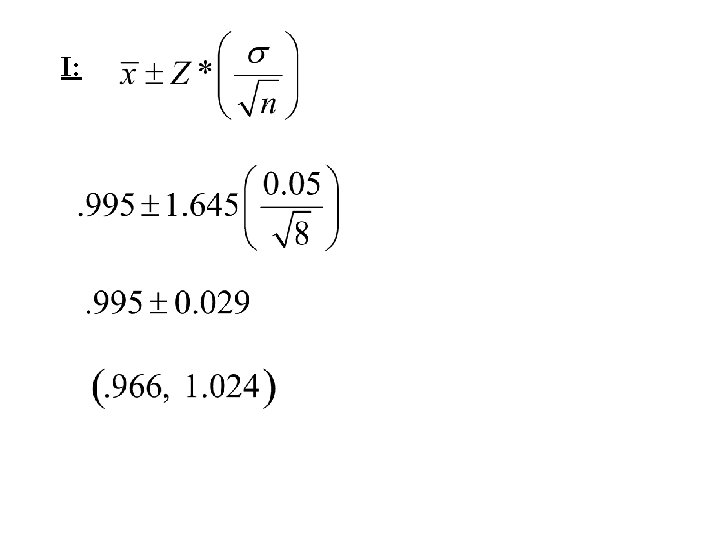
I:

C: I am 90% confident the true mean weight of Snickers 1 -oz Fun-size candy bars is between. 966 and 1. 024 ounces. I am confident that the candy bars weigh as advertised at the 90% level.

Example #3 A statistician calculates a 95% confidence interval for the mean income of the depositors at Bank of America, located in a poverty stricken area. The confidence interval is $18, 201 to $21, 799. a. What is the sample mean income?

Example #3 A statistician calculates a 95% confidence interval for the mean income of the depositors at Bank of America, located in a poverty stricken area. The confidence interval is $18, 201 to $21, 799. b. What is the margin of error? m m = 21, 799 – 20, 000 m = 1, 799

Choosing a Sample Size for a specific margin of error Note: Always round up! You can’t have part of a person! Ex: 163. 2 rounds up to 164.

Example #4 A researcher wishes to estimate the mean number of miles on four-year-old Saturn SCI’s. How many cars should be in a sample in order to estimate the mean number of miles within a margin of error of 1000 miles with 99% confidence assuming =19, 700.