Chapter 9 Estimating the Value of a Parameter


















- Slides: 27

Chapter 9 Estimating the Value of a Parameter Using Confidence Intervals © 2010 Pearson Prentice Hall. All rights reserved

Section 9. 2 Confidence Intervals about a Population Mean When the Population Standard Deviation is Unknown © 2010 Pearson Prentice Hall. All rights reserved

Objectives 1. Know the properties of Student’s t-distribution 2. Determine t-values 3. Construct and interpret a confidence interval for a population mean © 2010 Pearson Prentice Hall. All rights reserved 9 -3

Objective 1 • Know the Properties of Student’s t-Distribution © 2010 Pearson Prentice Hall. All rights reserved 9 -4

Student’s t-Distribution Suppose that a simple random sample of size n is taken from a population. If the population from which the sample is drawn follows a normal distribution, the distribution of follows Student’s t-distribution with n-1 degrees of freedom where is the sample mean and s is the sample standard deviation. © 2010 Pearson Prentice Hall. All rights reserved 9 -5

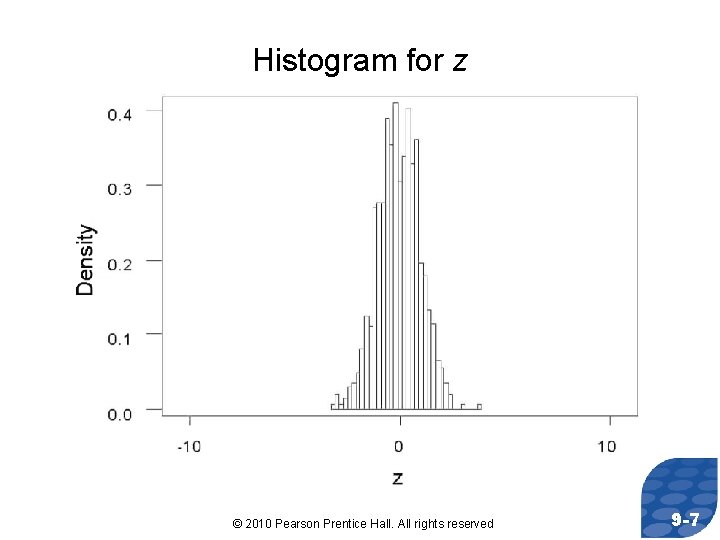
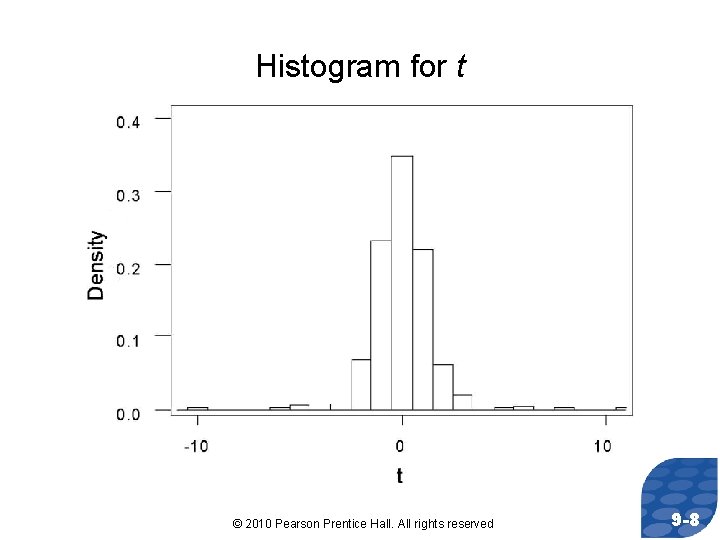
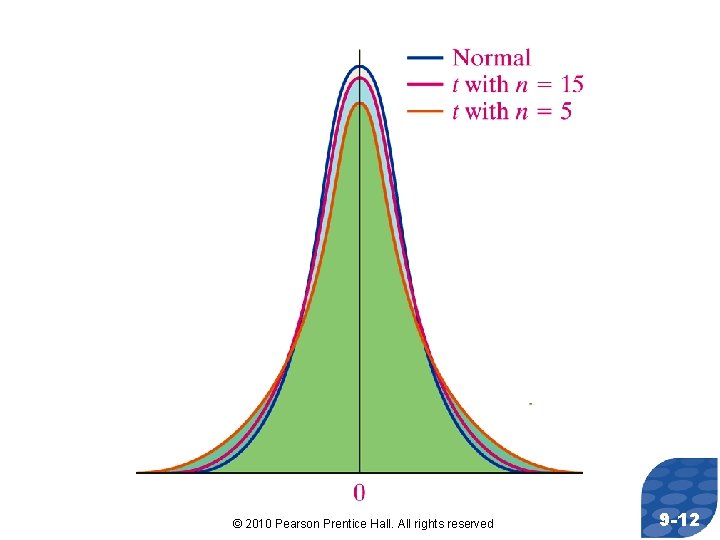
Parallel Example 1: Comparing the Standard Normal Distribution to the t-Distribution Using Simulation a) Obtain 1, 000 simple random samples of size n=5 from a normal population with =50 and =10. b) Determine the sample mean and sample standard deviation for each of the samples. c) Compute and for each sample. d) Draw a histogram for both z and t. © 2010 Pearson Prentice Hall. All rights reserved 9 -6

Histogram for z © 2010 Pearson Prentice Hall. All rights reserved 9 -7

Histogram for t © 2010 Pearson Prentice Hall. All rights reserved 9 -8

CONCLUSIONS: • The histogram for z is symmetric and bell-shaped with the center of the distribution at 0 and virtually all the rectangles between -3 and 3. In other words, z follows a standard normal distribution. • The histogram for t is also symmetric and bell-shaped with the center of the distribution at 0, but the distribution of t has longer tails (i. e. , t is more dispersed), so it is unlikely that t follows a standard normal distribution. The additional spread in the distribution of t can be attributed to the fact that we use s to find t instead of . Because the sample standard deviation is itself a random variable (rather than a constant such as ), we have more dispersion in the distribution of t. © 2010 Pearson Prentice Hall. All rights reserved 9 -9

Properties of the t-Distribution 1. The t-distribution is different for different degrees of freedom. 2. The t-distribution is centered at 0 and is symmetric about 0. 3. The area under the curve is 1. The area under the curve to the right of 0 equals the area under the curve to the left of 0 equals 1/2. 4. As t increases without bound, the graph approaches, but never equals, zero. As t decreases without bound, the graph approaches, but never equals, zero. © 2010 Pearson Prentice Hall. All rights reserved 9 -10

Properties of the t-Distribution 5. The area in the tails of the t-distribution is a little greater than the area in the tails of the standard normal distribution, because we are using s as an estimate of , thereby introducing further variability into the tstatistic. 6. As the sample size n increases, the density curve of t gets closer to the standard normal density curve. This result occurs because, as the sample size n increases, the values of s get closer to the values of , by the Law of Large Numbers. © 2010 Pearson Prentice Hall. All rights reserved 9 -11

© 2010 Pearson Prentice Hall. All rights reserved 9 -12

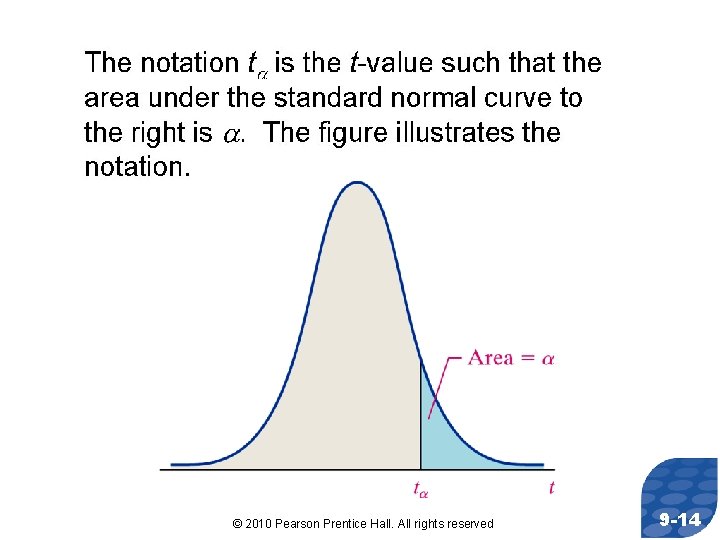
Objective 2 • Determine t-Values © 2010 Pearson Prentice Hall. All rights reserved 9 -13

© 2010 Pearson Prentice Hall. All rights reserved 9 -14

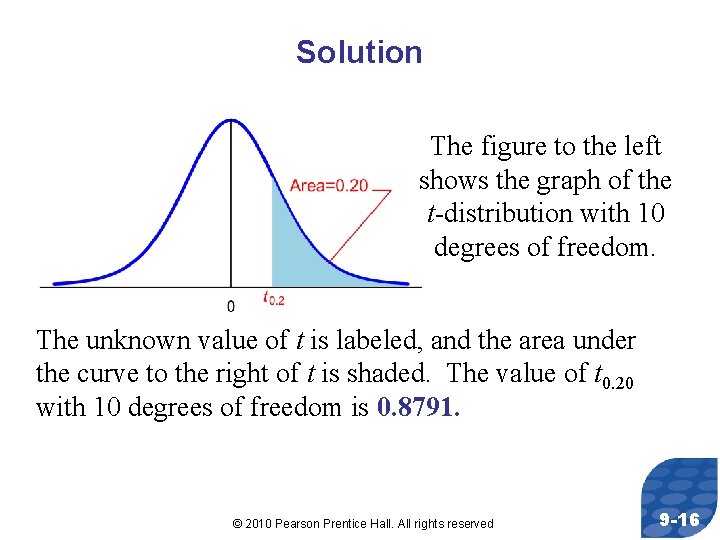
Parallel Example 2: Finding t-values Find the t-value such that the area under the tdistribution to the right of the t-value is 0. 2 assuming 10 degrees of freedom. That is, find t 0. 20 with 10 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 9 -15

Solution The figure to the left shows the graph of the t-distribution with 10 degrees of freedom. The unknown value of t is labeled, and the area under the curve to the right of t is shaded. The value of t 0. 20 with 10 degrees of freedom is 0. 8791. © 2010 Pearson Prentice Hall. All rights reserved 9 -16

Objective 3 • Construct and Interpret a Confidence Interval for a Population Mean © 2010 Pearson Prentice Hall. All rights reserved 9 -17

Constructing a (1 - ) 100% Confidence Interval for , Unknown Suppose that a simple random sample of size n is taken from a population with unknown mean and unknown standard deviation . A (1 - ) 100% confidence interval for is given by Lower bound: Upper bound: Note: The interval is exact when the population is normally distributed. It is approximately correct for nonnormal populations, provided that n is large enough. © 2010 Pearson Prentice Hall. All rights reserved 9 -18

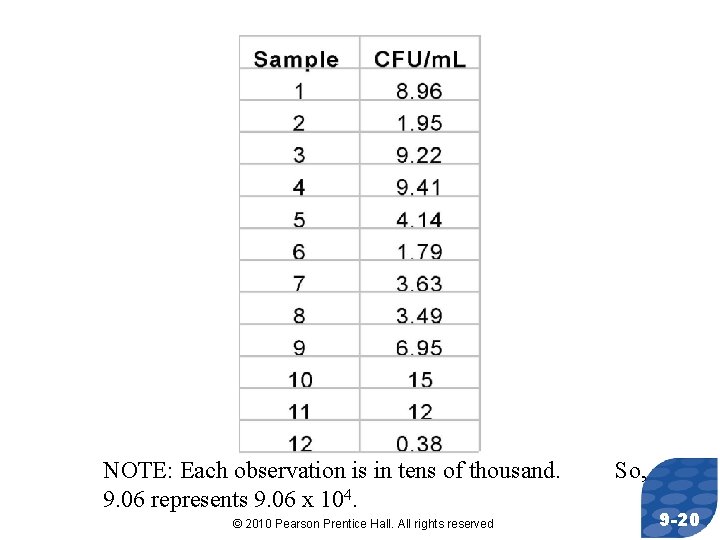
Parallel Example 3: Constructing a Confidence Interval about a Population Mean The pasteurization process reduces the amount of bacteria found in dairy products, such as milk. The following data represent the counts of bacteria in pasteurized milk (in CFU/m. L) for a random sample of 12 pasteurized glasses of milk. Data courtesy of Dr. Michael Lee, Professor, Joliet Junior College. Construct a 95% confidence interval for the bacteria count. © 2010 Pearson Prentice Hall. All rights reserved 9 -19

NOTE: Each observation is in tens of thousand. 9. 06 represents 9. 06 x 104. © 2010 Pearson Prentice Hall. All rights reserved So, 9 -20

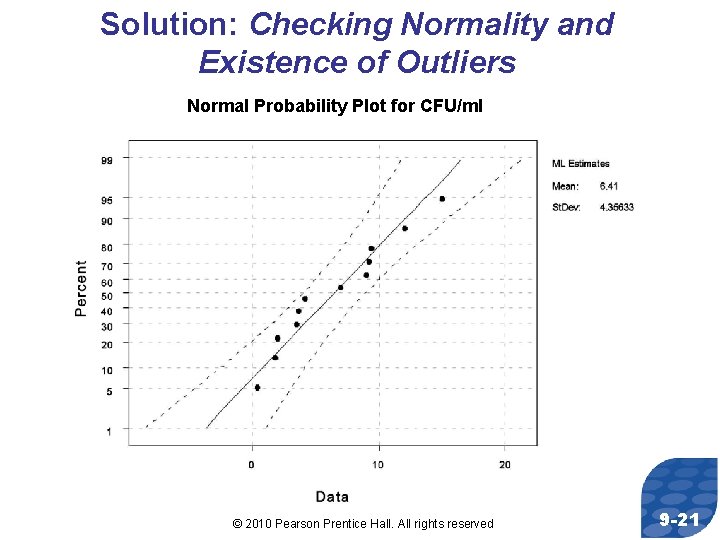
Solution: Checking Normality and Existence of Outliers Normal Probability Plot for CFU/ml © 2010 Pearson Prentice Hall. All rights reserved 9 -21

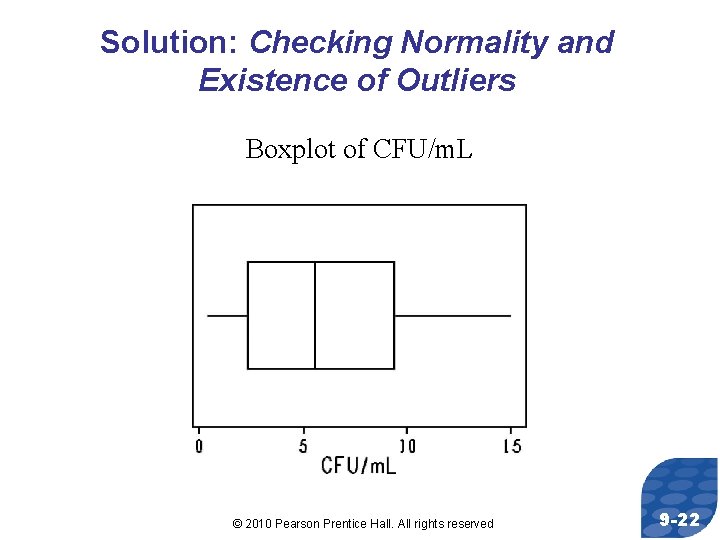
Solution: Checking Normality and Existence of Outliers Boxplot of CFU/m. L © 2010 Pearson Prentice Hall. All rights reserved 9 -22

• • Lower bound: Upper bound: The 95% confidence interval for the mean bacteria count in pasteurized milk is (3. 52, 9. 30). © 2010 Pearson Prentice Hall. All rights reserved 9 -23

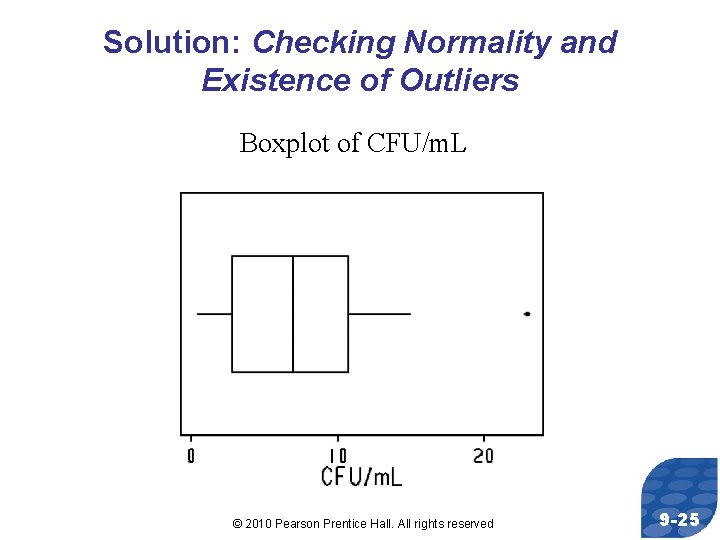
Parallel Example 5: The Effect of Outliers Suppose a student miscalculated the amount of bacteria and recorded a result of 2. 3 x 105. We would include this value in the data set as 23. 0. What effect does this additional observation have on the 95% confidence interval? © 2010 Pearson Prentice Hall. All rights reserved 9 -24

Solution: Checking Normality and Existence of Outliers Boxplot of CFU/m. L © 2010 Pearson Prentice Hall. All rights reserved 9 -25

Solution • • Lower bound: Upper bound: The 95% confidence interval for the mean bacteria count in pasteurized milk, including the outlier is (3. 86, 11. 52). © 2010 Pearson Prentice Hall. All rights reserved 9 -26

CONCLUSIONS: • With the outlier, the sample mean is larger because the sample mean is not resistant • With the outlier, the sample standard deviation is larger because the sample standard deviation is not resistant • Without the outlier, the width of the interval decreased from 7. 66 to 5. 78. s 95% CI Without Outlier 6. 41 4. 55 (3. 52, 9. 30) With Outlier 7. 69 6. 34 (3. 86, 11. 52) © 2010 Pearson Prentice Hall. All rights reserved 9 -27
 Place value and estimating
Place value and estimating Apa itu value creation
Apa itu value creation Readonly struct
Readonly struct Chapter 8 estimating with confidence
Chapter 8 estimating with confidence Suppose your class is investigating the weights of snickers
Suppose your class is investigating the weights of snickers Chapter 8 estimating with confidence
Chapter 8 estimating with confidence Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Slidetodoc
Slidetodoc Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Tư thế worms-breton
Tư thế worms-breton Hát lên người ơi
Hát lên người ơi Các môn thể thao bắt đầu bằng tiếng nhảy
Các môn thể thao bắt đầu bằng tiếng nhảy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công của trọng lực
Công của trọng lực Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Bàn tay mà dây bẩn
Bàn tay mà dây bẩn Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ