TRANSFORMACIONES GEOMTRICAS EN EL PLANO R 2 ECUACIONES

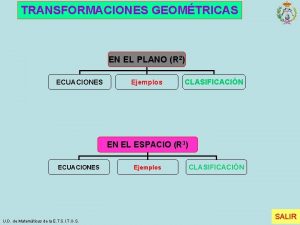
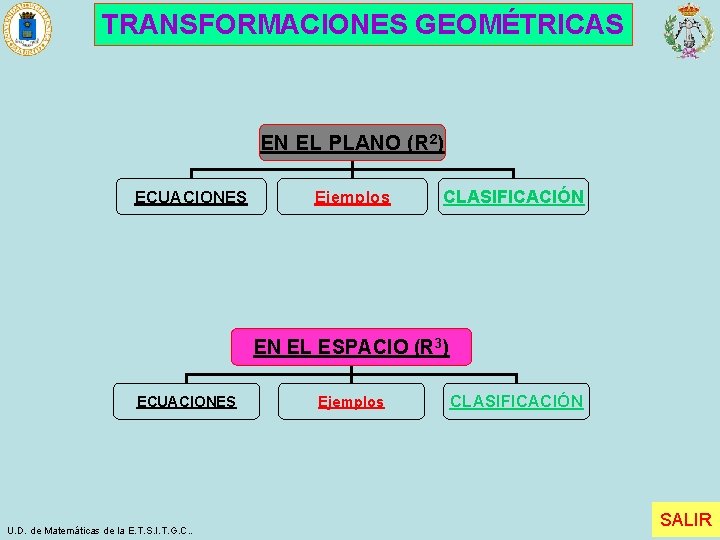
TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO (R 2) ECUACIONES Ejemplos CLASIFICACIÓN EN EL ESPACIO (R 3) ECUACIONES U. D. de Matemáticas de la E. T. S. I. T. G. C. . Ejemplos CLASIFICACIÓN Índice SALIR

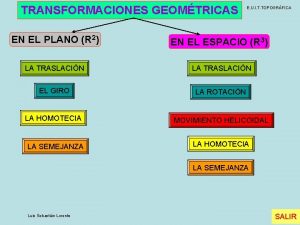
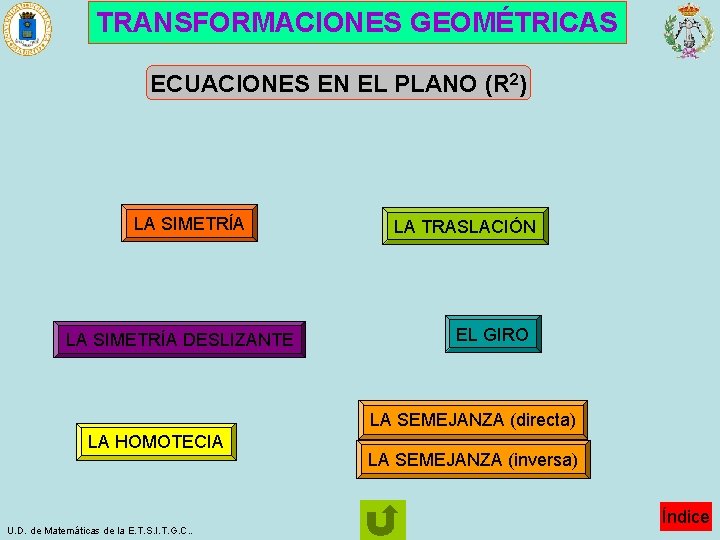
TRANSFORMACIONES GEOMÉTRICAS ECUACIONES EN EL PLANO (R 2) LA SIMETRÍA DESLIZANTE LA TRASLACIÓN EL GIRO LA SEMEJANZA (directa) LA HOMOTECIA U. D. de Matemáticas de la E. T. S. I. T. G. C. . LA SEMEJANZA (inversa) Índice

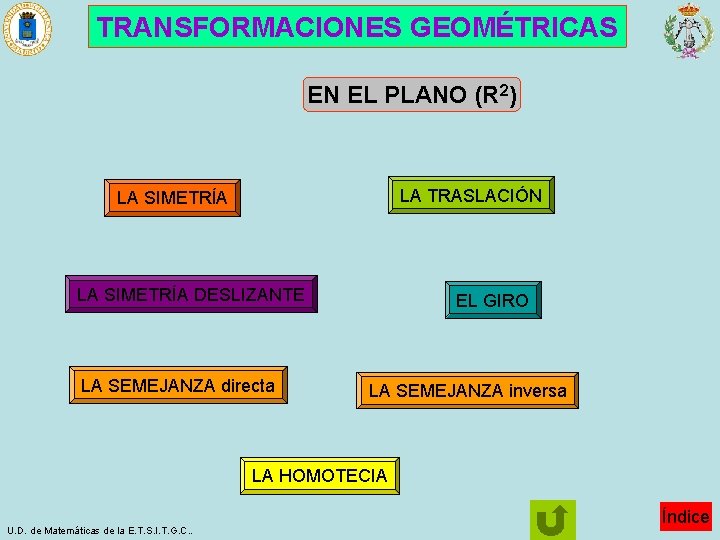
TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO (R 2) LA TRASLACIÓN LA SIMETRÍA DESLIZANTE LA SEMEJANZA directa EL GIRO LA SEMEJANZA inversa LA HOMOTECIA U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

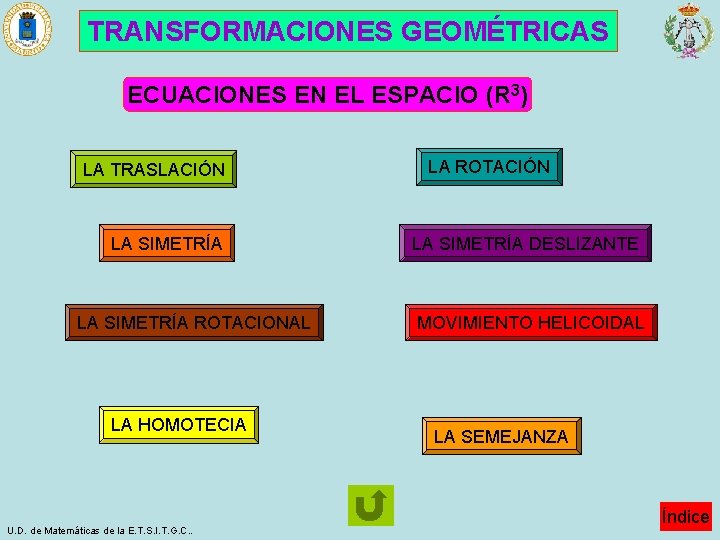
TRANSFORMACIONES GEOMÉTRICAS ECUACIONES EN EL ESPACIO (R 3) LA TRASLACIÓN LA SIMETRÍA ROTACIONAL LA HOMOTECIA U. D. de Matemáticas de la E. T. S. I. T. G. C. . LA ROTACIÓN LA SIMETRÍA DESLIZANTE MOVIMIENTO HELICOIDAL LA SEMEJANZA Índice

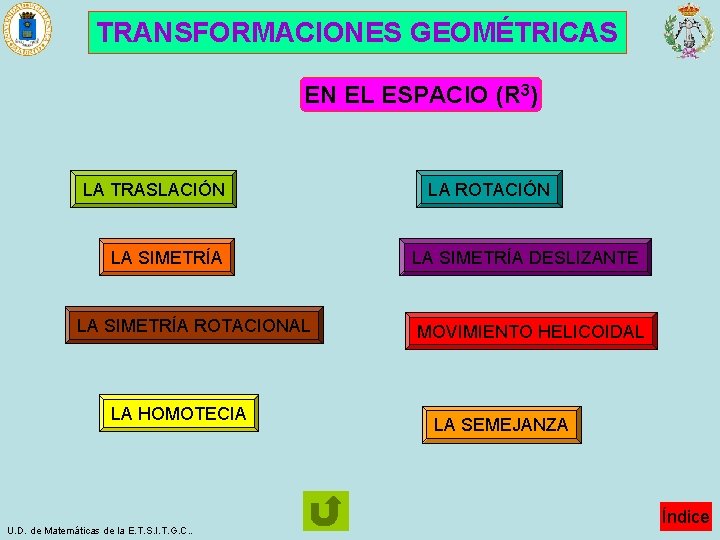
TRANSFORMACIONES GEOMÉTRICAS EN EL ESPACIO (R 3) LA TRASLACIÓN LA SIMETRÍA ROTACIONAL LA HOMOTECIA U. D. de Matemáticas de la E. T. S. I. T. G. C. . LA ROTACIÓN LA SIMETRÍA DESLIZANTE MOVIMIENTO HELICOIDAL LA SEMEJANZA Índice

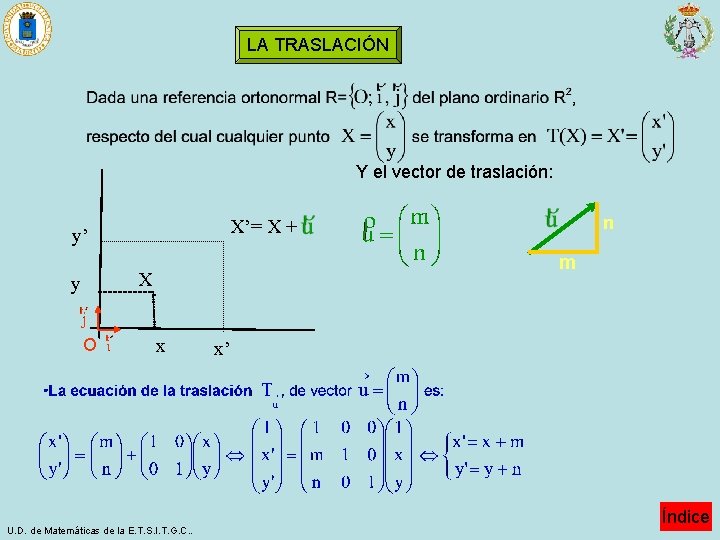
LA TRASLACIÓN Y el vector de traslación: m X y n X’= X + y’ · O x U. D. de Matemáticas de la E. T. S. I. T. G. C. . x’ Índice

El vector que define una traslación es (-2, 3). Se pide: a) Ecuación de la traslación. b) Coordenadas del transformado del punto A(1, 2). c) Ecuación de la circunferencia transformada de x 2+y 2 -2 x-4 y=0. d) La transformada de la recta x/3+y/2=1. U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

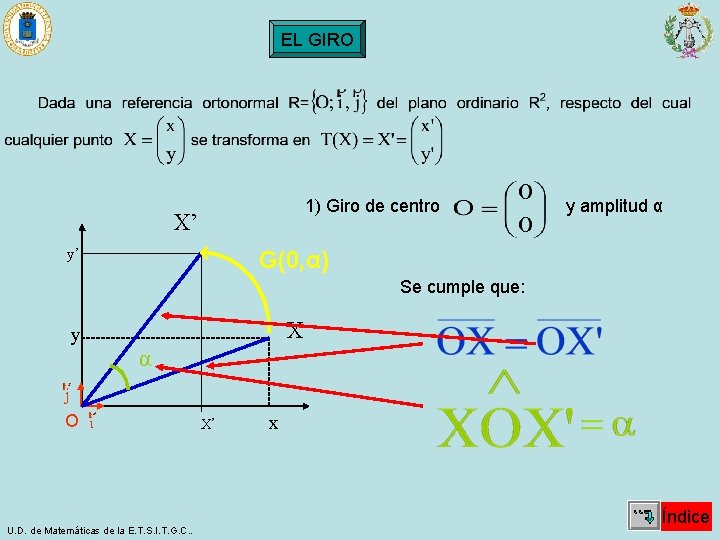
EL GIRO 1) Giro de centro X’ y’ y amplitud α G(0, α) Se cumple que: y X α O U. D. de Matemáticas de la E. T. S. I. T. G. C. . X’ x Índice

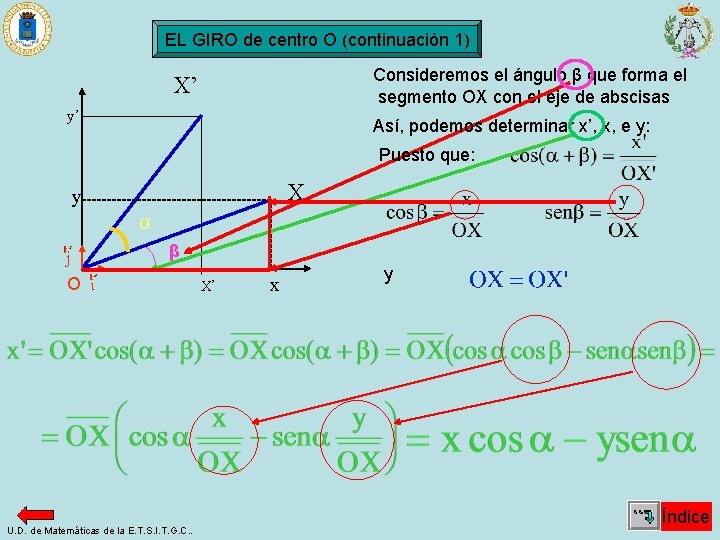
EL GIRO de centro O (continuación 1) Consideremos el ángulo β que forma el segmento OX con el eje de abscisas X’ y’ Así, podemos determinar x’, x, e y: Puesto que: y X α β O U. D. de Matemáticas de la E. T. S. I. T. G. C. . X’ x y Índice

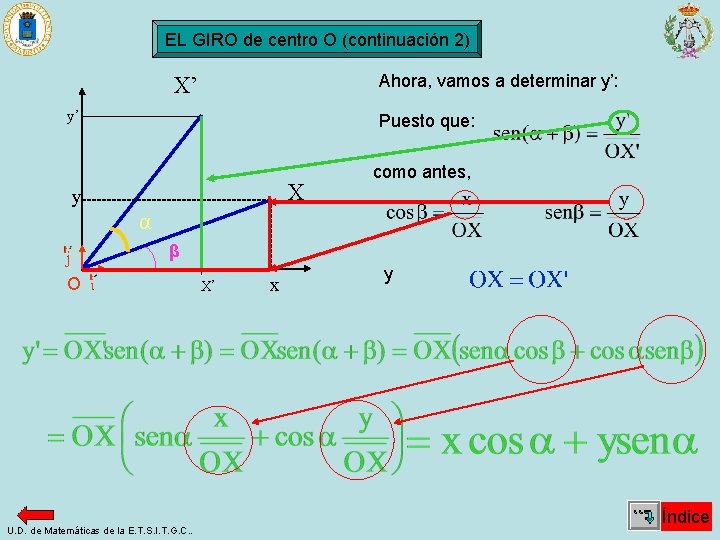
EL GIRO de centro O (continuación 2) Ahora, vamos a determinar y’: X’ y’ y Puesto que: X como antes, α β O U. D. de Matemáticas de la E. T. S. I. T. G. C. . X’ x y Índice

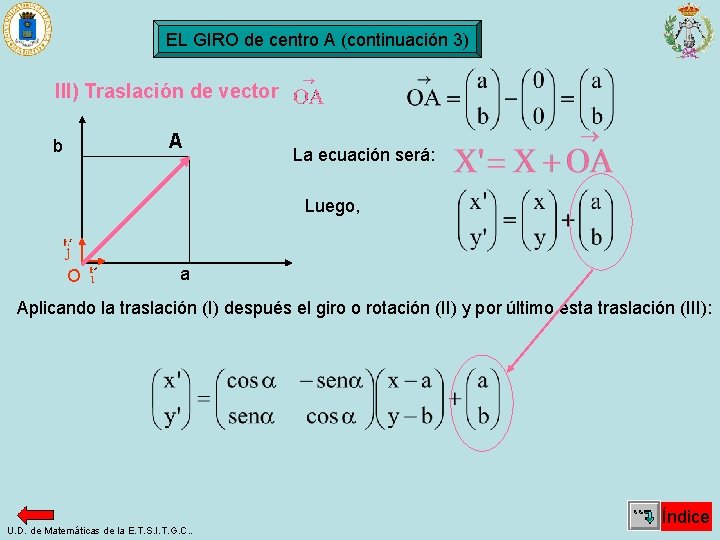
EL GIRO de centro O (continuación 3) Veamos, ahora, para cualquier centro A(a, b): U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

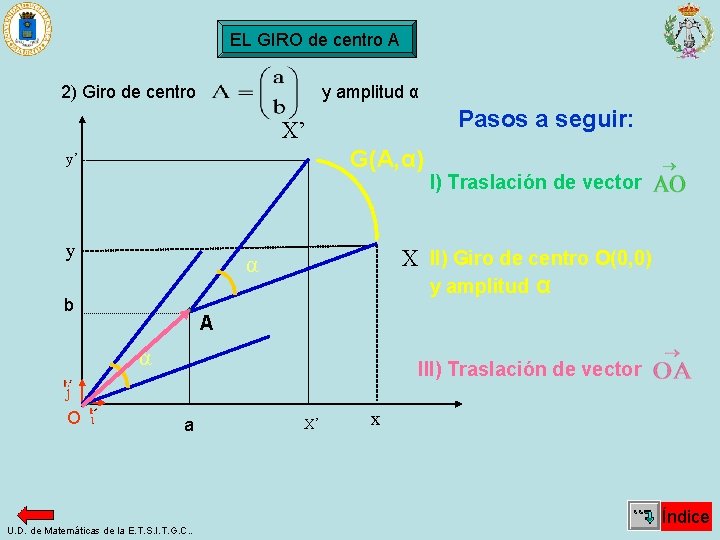
EL GIRO de centro A 2) Giro de centro y amplitud α Pasos a seguir: X’ G(A, α) y’ y X II) Giro de centro O(0, 0) y amplitud α α b A α O I) Traslación de vector III) Traslación de vector a U. D. de Matemáticas de la E. T. S. I. T. G. C. . X’ x Índice

EL GIRO de centro A (continuación 1) I) Traslación de vector b O ; siendo A a La ecuación será: Luego, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

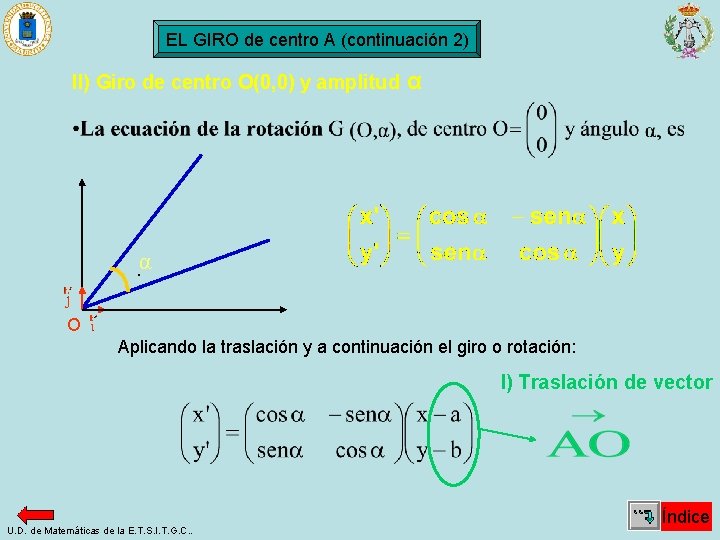
EL GIRO de centro A (continuación 2) II) Giro de centro O(0, 0) y amplitud α α · O Aplicando la traslación y a continuación el giro o rotación: I) Traslación de vector U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

EL GIRO de centro A (continuación 3) III) Traslación de vector A b La ecuación será: Luego, O a Aplicando la traslación (I) después el giro o rotación (II) y por último esta traslación (III): U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

EL GIRO de centro A (continuación 4) O bien, Un caso particular es la simetría central que resulta cuando el ángulo de giro es 180º: U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Aplicando el giro al centro de la circunferencia O(2, 0) se obtiene: resulta la circunferencia: Análogamente, se haría para -60º U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

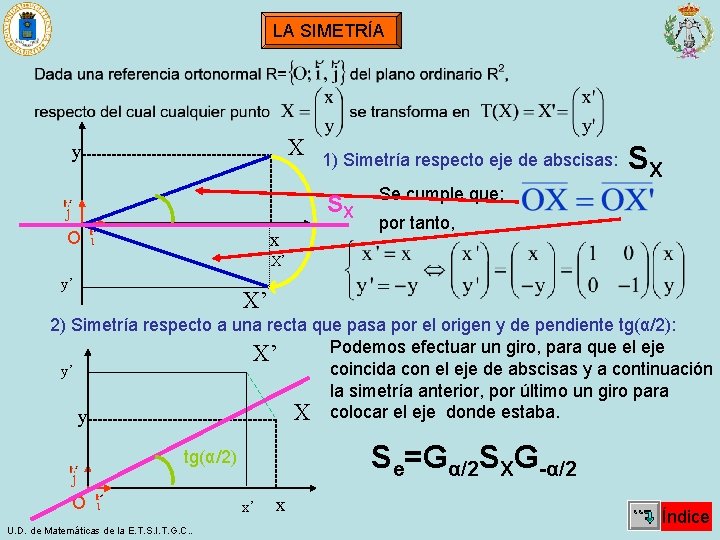
LA SIMETRÍA X y 1) Simetría respecto eje de abscisas: SX O x SX Se cumple que: por tanto, X’ y’ X’ 2) Simetría respecto a una recta que pasa por el origen y de pendiente tg(α/2): Podemos efectuar un giro, para que el eje X’ coincida con el eje de abscisas y a continuación y’ la simetría anterior, por último un giro para X colocar el eje donde estaba. y Se=Gα/2 SXG-α/2 tg(α/2) O U. D. de Matemáticas de la E. T. S. I. T. G. C. . x’ x Índice

LA SIMETRÍA (continuación 1) 2) Simetría respecto a una recta e. O que pasa por el origen y de pendiente tg(α/2): I) Giro de centro e. O y amplitud -α/2: X y tg(α/2) G(0, α/2) O x II) Simetría respecto eje de abscisas: III) Giro de centro y amplitud α/2: Por tanto, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

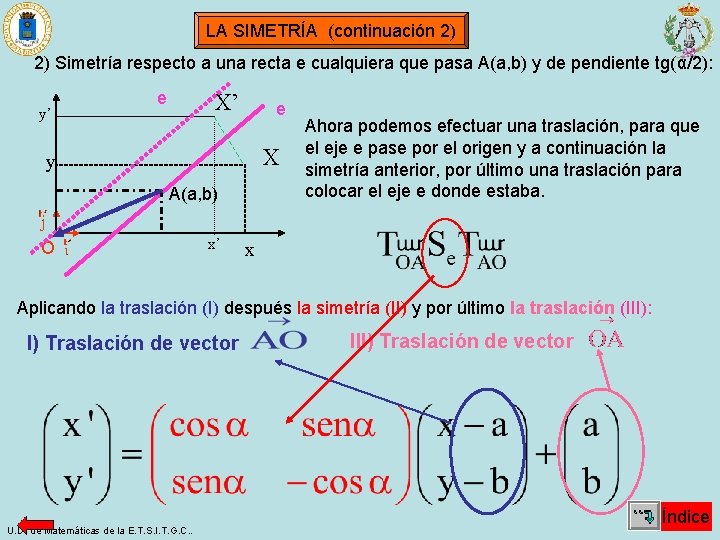
LA SIMETRÍA (continuación 2) 2) Simetría respecto a una recta e cualquiera que pasa A(a, b) y de pendiente tg(α/2): y’ e X y A(a, b) O x’ Ahora podemos efectuar una traslación, para que el eje e pase por el origen y a continuación la simetría anterior, por último una traslación para colocar el eje e donde estaba. x Aplicando la traslación (I) después la simetría (II) y por último la traslación (III): I) Traslación de vector U. D. de Matemáticas de la E. T. S. I. T. G. C. . III) Traslación de vector Índice

LA SIMETRÍA (continuación 3) O bien, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

b) Para transformar una recta (en general, una ecuación) debemos despejar x e y; en este caso, por ser una simetría, queda igual: Para la recta r: 3 x+4 y=0, se tiene: Para la recta t: x+y=1, se tiene: U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

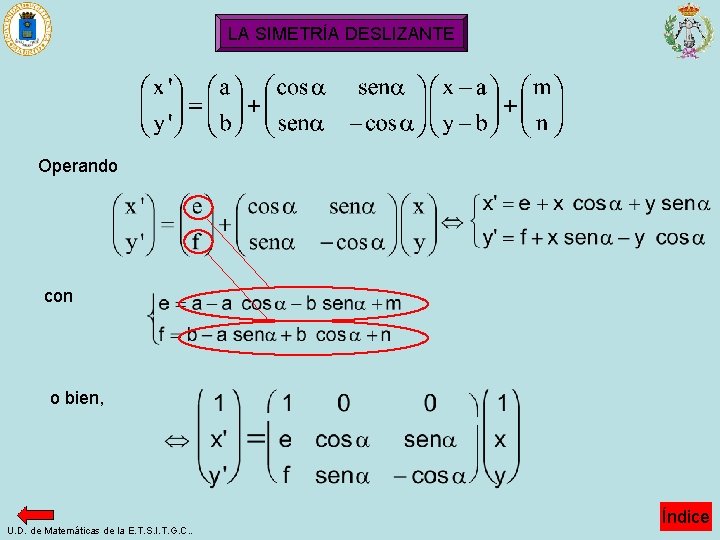
LA SIMETRÍA DESLIZANTE X e X’ U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

LA SIMETRÍA DESLIZANTE Operando con o bien, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

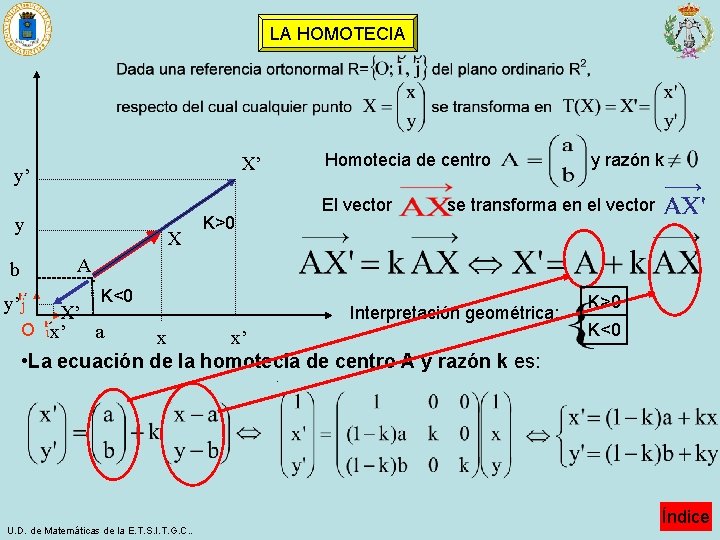
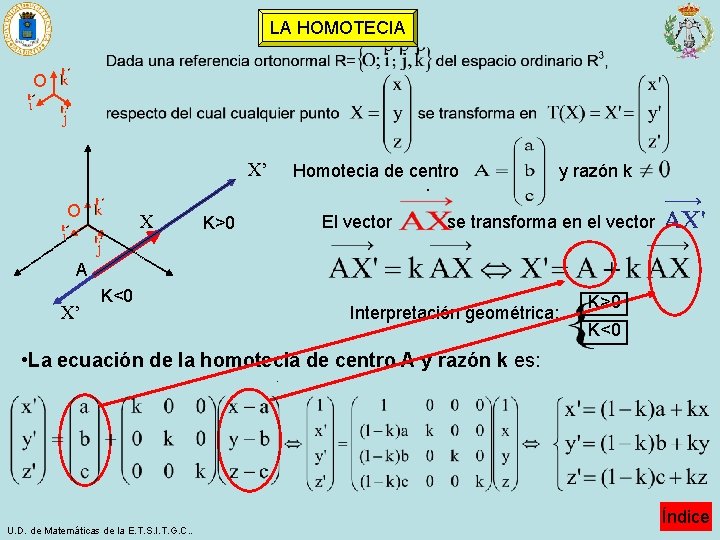
LA HOMOTECIA y’ y b y’ Homotecia de centro X’ X El vector K>0 y razón k se transforma en el vector A · K<0 X’ Interpretación geométrica: O x’ a x’ x • La ecuación de la homotecia de centro A y razón k es: K>0 K<0 . U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

El baricentro se encuentra a un tercio de la base y 2/3 del vértice. Se trata de encontrar las ecuaciones de una homotecia de centro O(0, 0) y razón k=1/3: G O’ Como C recorre una circunferencia el homotético de C, el baricentro recorre la circunferencia homotética, cuyos centros son homólogos. r’=k. r=(1/3). 3=1 centro de la circunferencia homotética de radio 1 U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

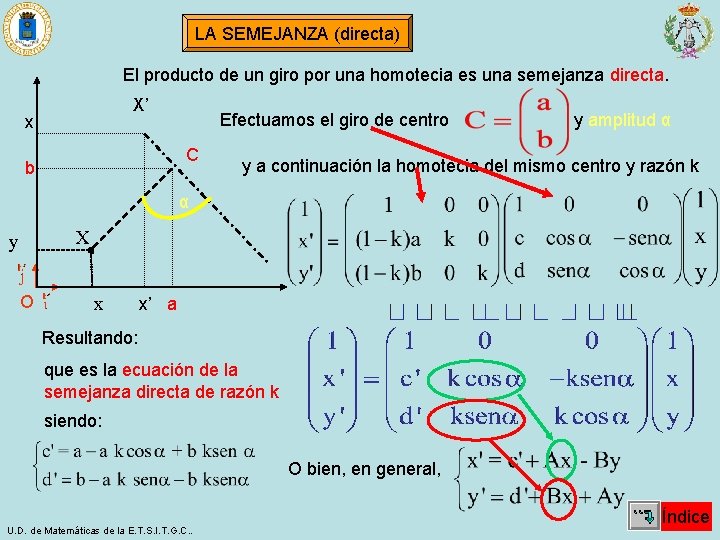
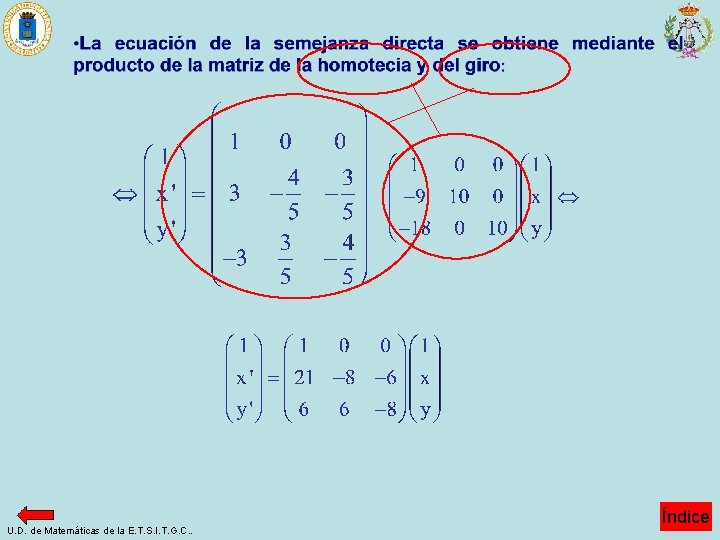
LA SEMEJANZA (directa) El producto de un giro por una homotecia es una semejanza directa. X’ x Efectuamos el giro de centro C b y amplitud α y a continuación la homotecia del mismo centro y razón k α X y · O x x’ a Resultando: que es la ecuación de la semejanza directa de razón k siendo: O bien, en general, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

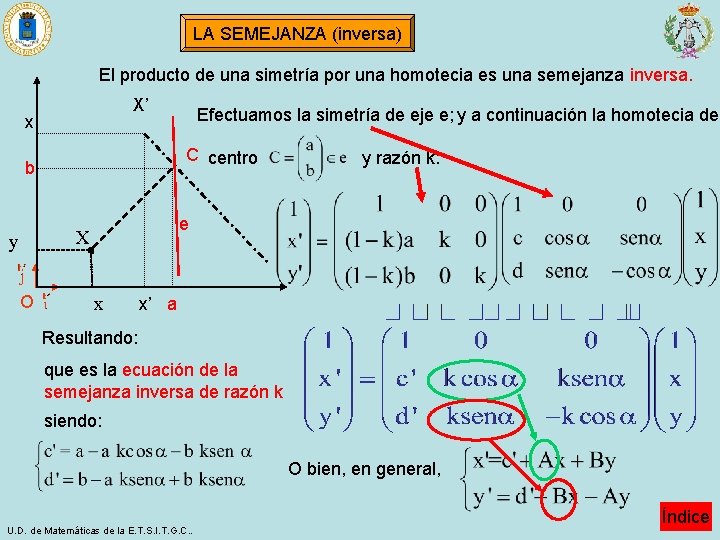
LA SEMEJANZA (inversa) El producto de una simetría por una homotecia es una semejanza inversa. X’ x C centro b y razón k: e X y Efectuamos la simetría de eje e; y a continuación la homotecia de · O x x’ a Resultando: que es la ecuación de la semejanza inversa de razón k siendo: O bien, en general, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

• La ecuación de la homotecia de centro A(1, 2) y razón 10 es: U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

• La ecuación de la homotecia de centro A(1, -1) y razón -2 es: U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

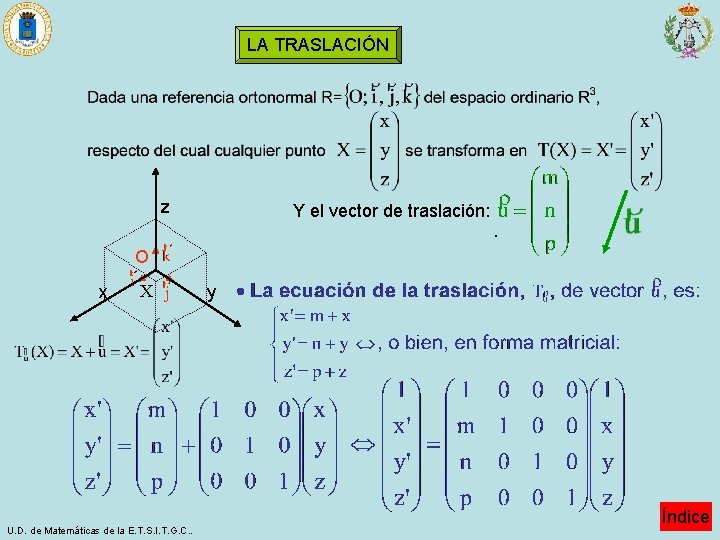
LA TRASLACIÓN z Y el vector de traslación: · O x X U. D. de Matemáticas de la E. T. S. I. T. G. C. . y Índice

Las ecuaciones de la recta r’, transformada de la recta r por la traslación: La ecuación del plano п’, transformado del plano п por la traslación: U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

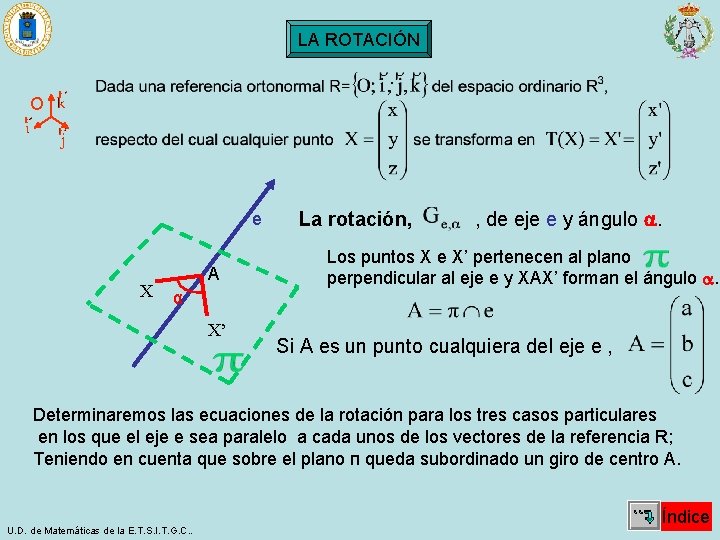
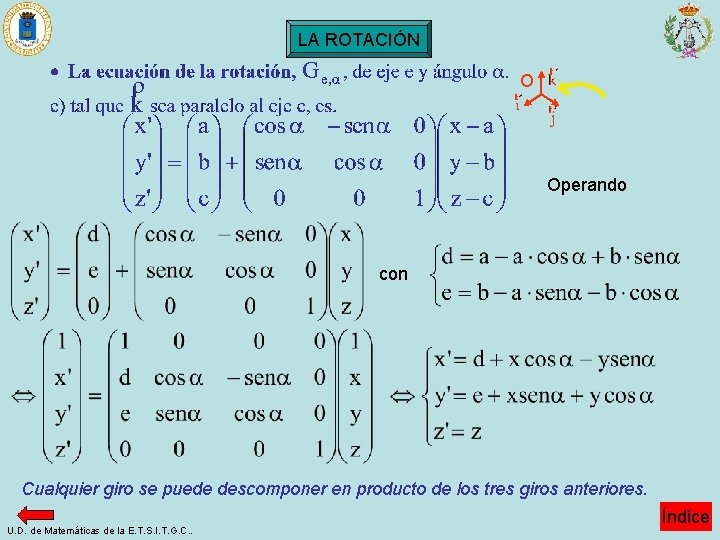
LA ROTACIÓN · O e X A α X’ La rotación, , de eje e y ángulo . Los puntos X e X’ pertenecen al plano perpendicular al eje e y XAX’ forman el ángulo . Si A es un punto cualquiera del eje e , Determinaremos las ecuaciones de la rotación para los tres casos particulares en los que el eje e sea paralelo a cada unos de los vectores de la referencia R; Teniendo en cuenta que sobre el plano п queda subordinado un giro de centro A. U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

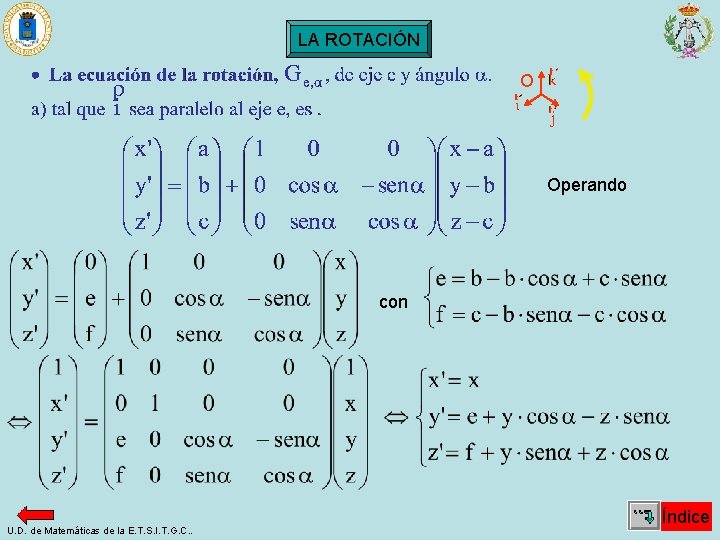
LA ROTACIÓN O Operando con U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

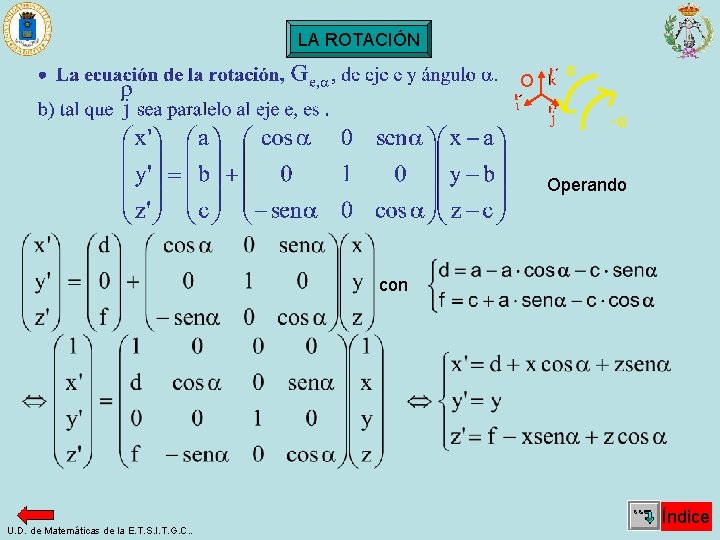
LA ROTACIÓN O α -α Operando con U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

LA ROTACIÓN O Operando con Cualquier giro se puede descomponer en producto de los tres giros anteriores. U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

en nuestro caso, por tanto, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

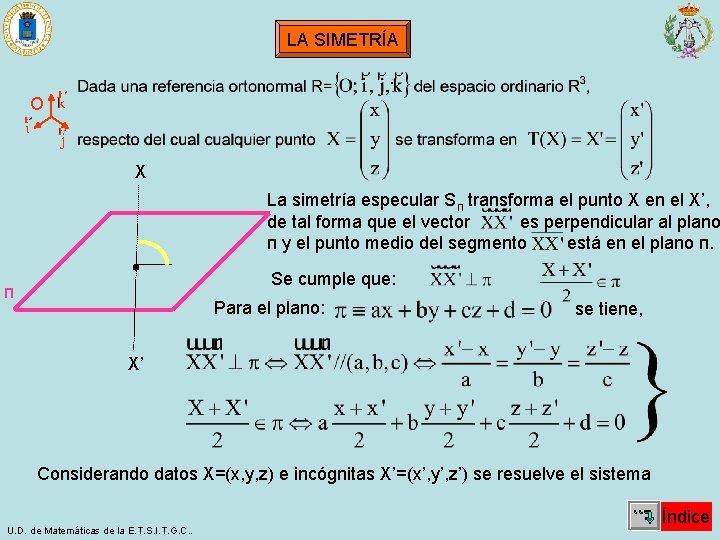
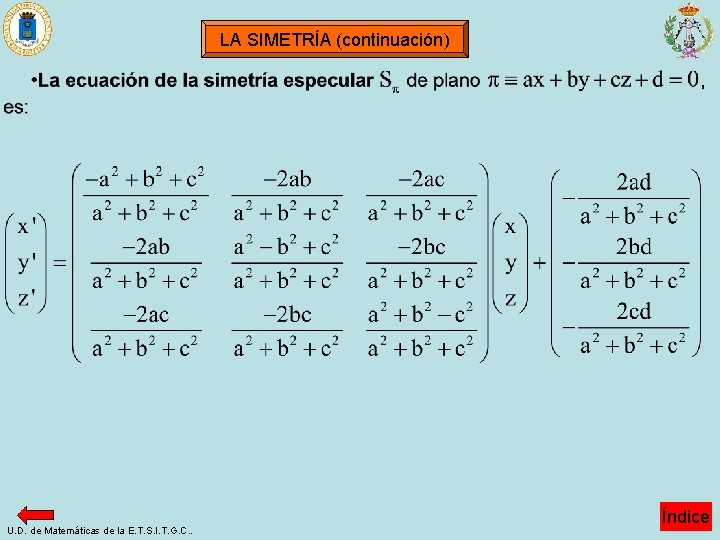
LA SIMETRÍA · O X La simetría especular Sп transforma el punto X en el X’, de tal forma que el vector es perpendicular al plano п y el punto medio del segmento está en el plano п. Se cumple que: п Para el plano: se tiene, X’ Considerando datos X=(x, y, z) e incógnitas X’=(x’, y’, z’) se resuelve el sistema U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

LA SIMETRÍA (continuación) U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Ecuaciones de la simetría especular respecto al plano x+y+z=0 Como, se tiene que cumplir: en nuestro caso: Considerando datos X=(x, y, z) e incógnitas X’=(x’, y’, z’) se resuelve el sistema U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

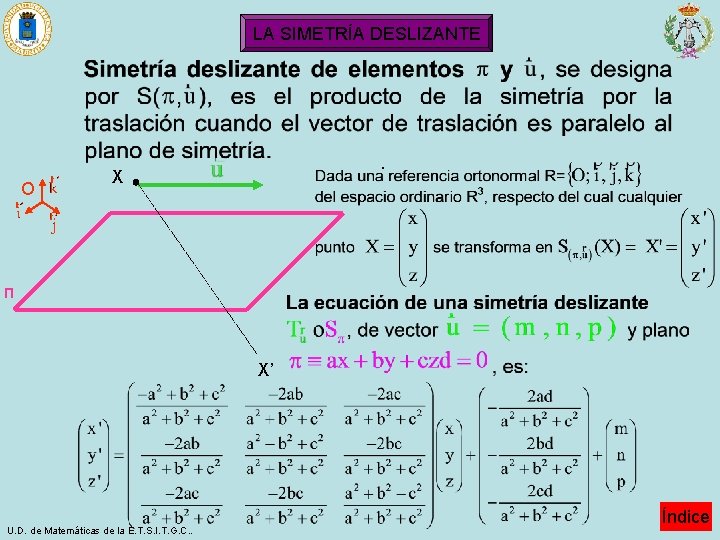
LA SIMETRÍA DESLIZANTE O · X п X’ U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Ecuaciones de la simetría deslizante de plano x+y+z=0 y vector (1, 0, -1). Las ecuaciones de la simetría especular son: véase el ejemplo y a continuación la traslación: U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

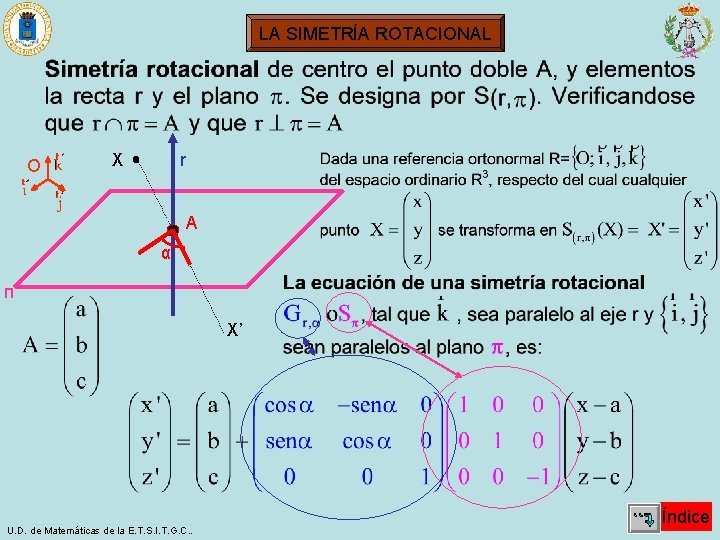
LA SIMETRÍA ROTACIONAL O X r A α п X’ U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

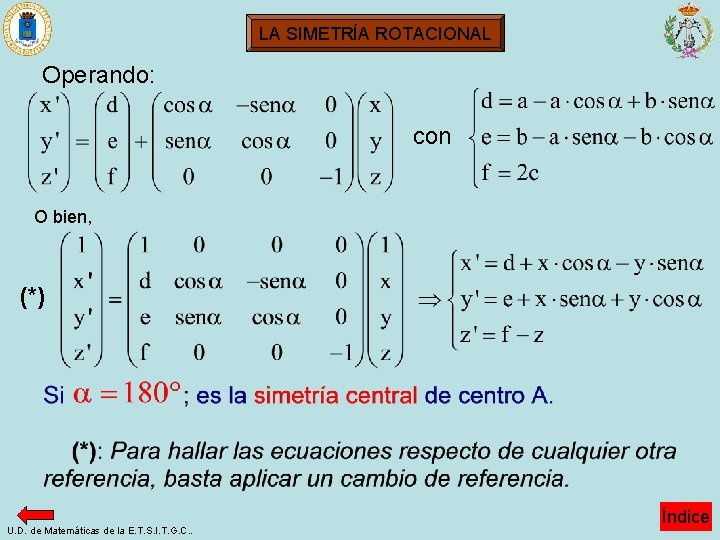
LA SIMETRÍA ROTACIONAL Operando: con O bien, (*) U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

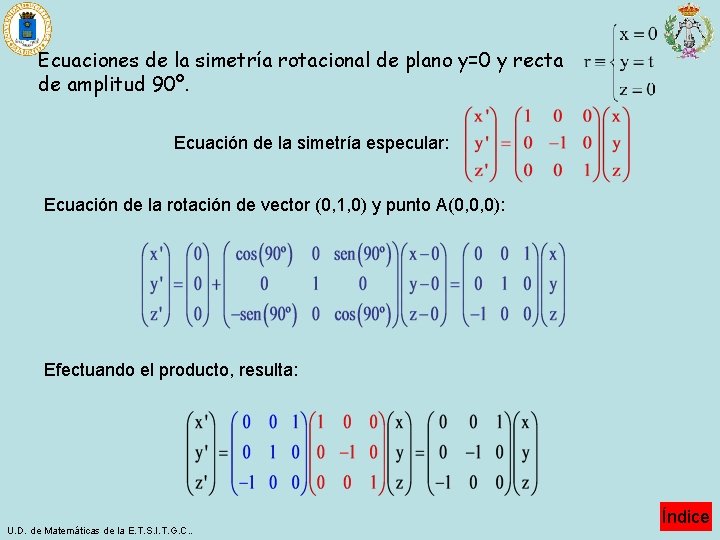
Ecuaciones de la simetría rotacional de plano y=0 y recta de amplitud 90º. Ecuación de la simetría especular: Ecuación de la rotación de vector (0, 1, 0) y punto A(0, 0, 0): Efectuando el producto, resulta: U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

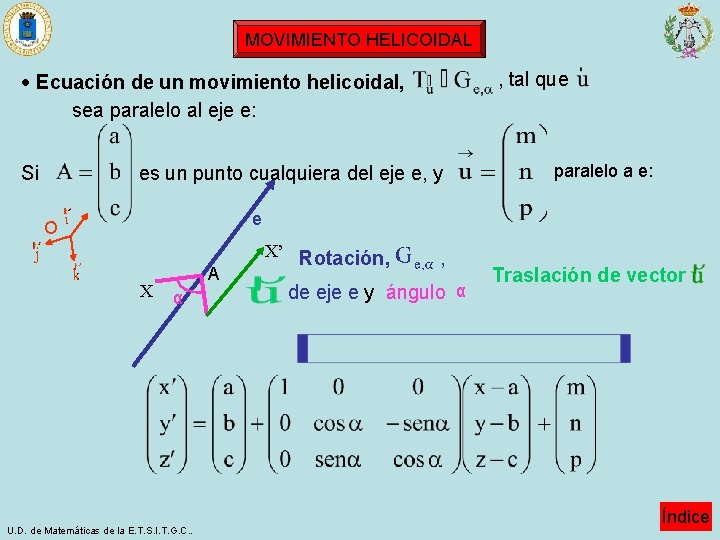
MOVIMIENTO HELICOIDAL , tal que Ecuación de un movimiento helicoidal, sea paralelo al eje e: Si es un punto cualquiera del eje e, y paralelo a e: e O X A α U. D. de Matemáticas de la E. T. S. I. T. G. C. . X’ Rotación, , de eje e y ángulo α Traslación de vector Índice

Ecuación de la traslación: Ecuación del giro: véase el ejemplo Ecuación de un movimiento helicoidal, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

LA HOMOTECIA · O X’ O X Homotecia de centro · El vector K>0 y razón k se transforma en el vector A X’ K<0 Interpretación geométrica: K>0 K<0 • La ecuación de la homotecia de centro A y razón k es: . U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Despejando, obtenemos la inversa de la Homotecia: Sustituyendo en la ecuación de la recta: U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

LA SEMEJANZA La semejanza se obtiene por el producto de las transformaciones anteriores. U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

La semejanza se obtiene por el producto de las transformaciones anteriores. O bien, U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

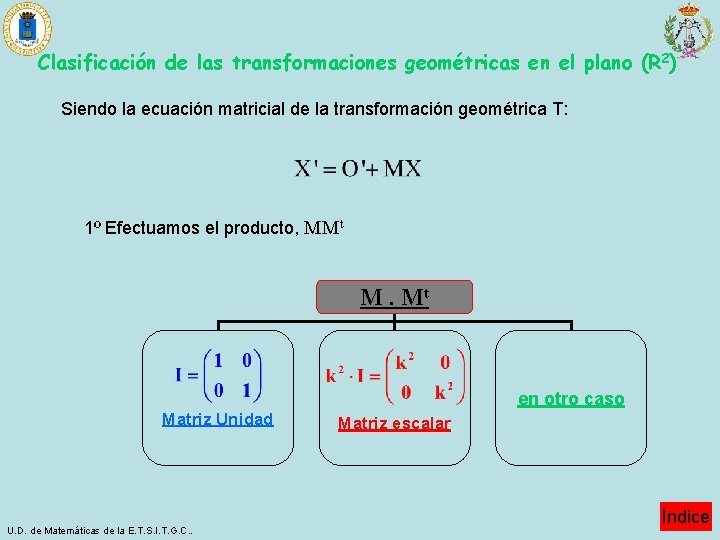
Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: 1º Efectuamos el producto, MMt M. Mt en otro caso Matriz Unidad U. D. de Matemáticas de la E. T. S. I. T. G. C. . Matriz escalar Índice

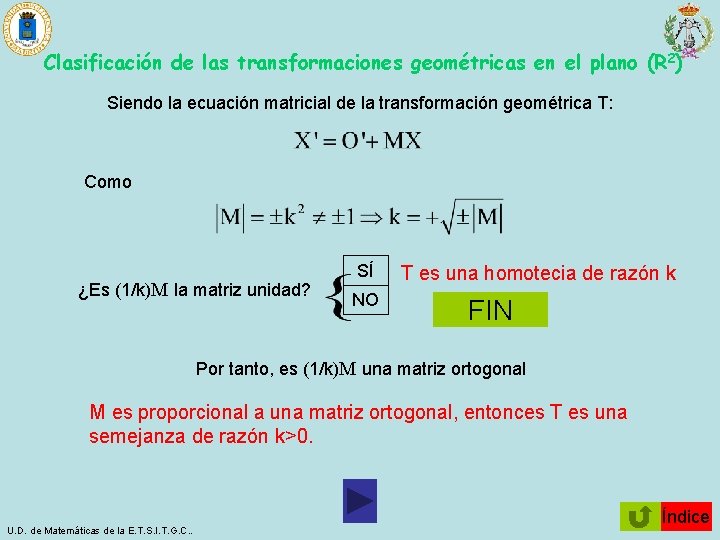
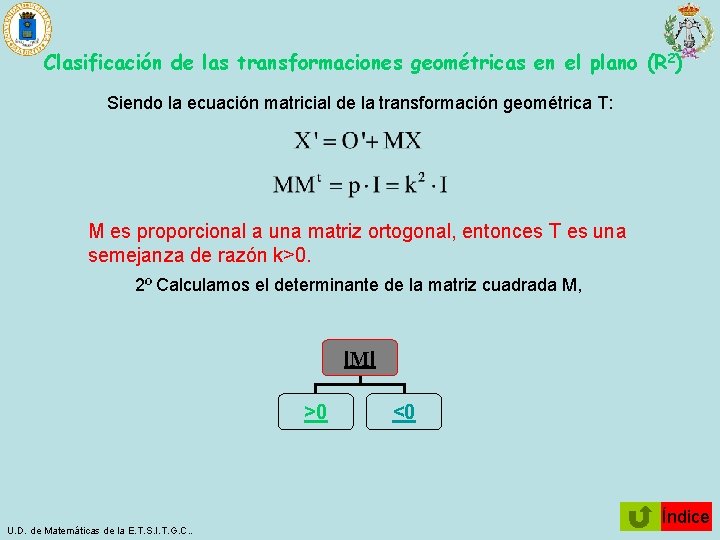
Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: Como ¿Es (1/k)M la matriz unidad? SÍ NO T es una homotecia de razón k FIN Por tanto, es (1/k)M una matriz ortogonal M es proporcional a una matriz ortogonal, entonces T es una semejanza de razón k>0. U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: M es proporcional a una matriz ortogonal, entonces T es una semejanza de razón k>0. 2º Calculamos el determinante de la matriz cuadrada M, IMI >0 U. D. de Matemáticas de la E. T. S. I. T. G. C. . <0 Índice

Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: T es un movimiento, ya que M es una matriz ortogonal. 2º Calculamos los puntos dobles, es decir, la solución al sistema: 3º Si es necesario, calculamos el determinante de la matriz cuadrada M: U. D. de Matemáticas de la E. T. S. I. T. G. C. . FIN Índice

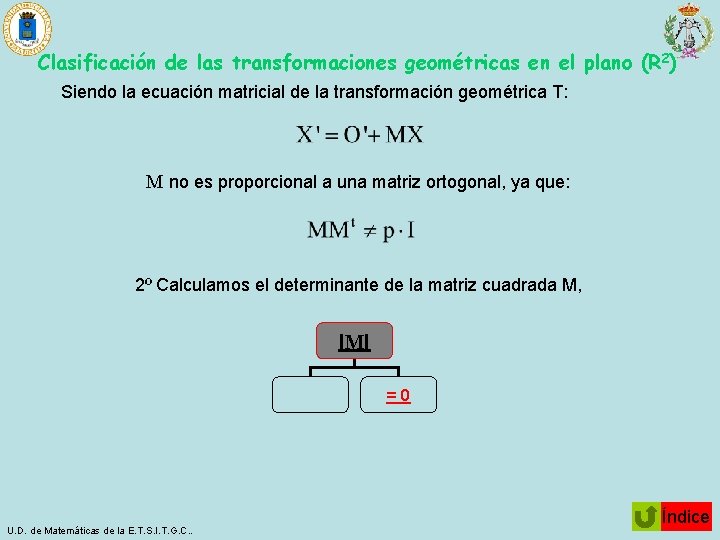
Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: M no es proporcional a una matriz ortogonal, ya que: 2º Calculamos el determinante de la matriz cuadrada M, IMI =0 U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: T no es biyectiva y por lo tanto no es una transformación geométrica. FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: M no es proporcional a una matriz ortogonal, entonces T es una transformación afín, no es una semejanza, ni un movimiento. FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el plano (R 2) Siendo la ecuación matricial de la transformación geométrica T: T no es biyectiva y por lo tanto no es una transformación geométrica. FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

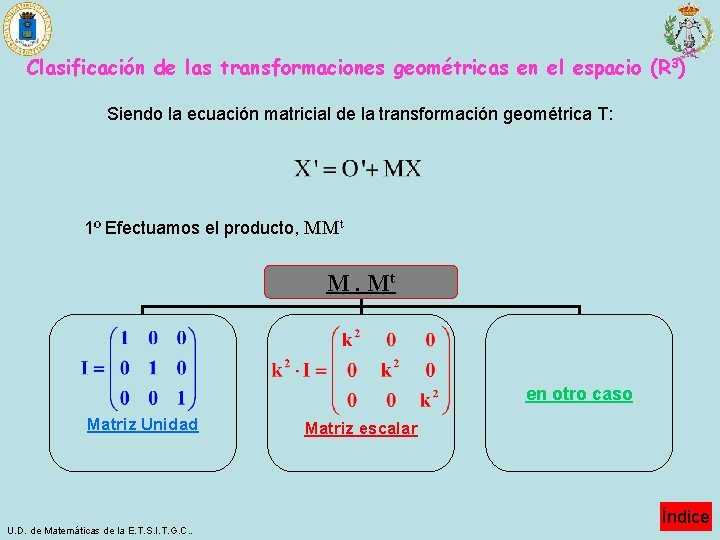
Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: 1º Efectuamos el producto, MMt M. Mt en otro caso Matriz Unidad U. D. de Matemáticas de la E. T. S. I. T. G. C. . Matriz escalar Índice

Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: T es un movimiento, ya que M es una matriz ortogonal. 2º Calculamos los puntos dobles, es decir, la solución al sistema: 3º Si es necesario, calculamos el determinante de la matriz cuadrada M: U. D. de Matemáticas de la E. T. S. I. T. G. C. . FIN Índice

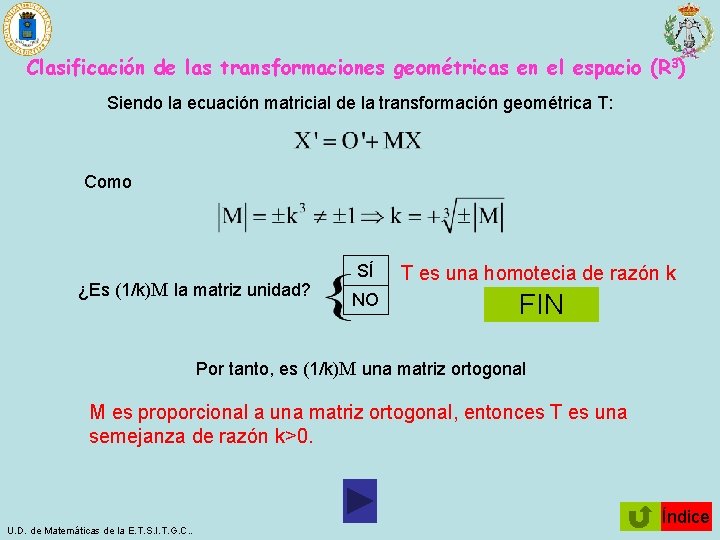
Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: Como ¿Es (1/k)M la matriz unidad? SÍ T es una homotecia de razón k NO FIN Por tanto, es (1/k)M una matriz ortogonal M es proporcional a una matriz ortogonal, entonces T es una semejanza de razón k>0. U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: M es proporcional a una matriz ortogonal, entonces T es una semejanza de razón k>0. 2º Calculamos el determinante de la matriz cuadrada M, IMI >0 U. D. de Matemáticas de la E. T. S. I. T. G. C. . <0 Índice

Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

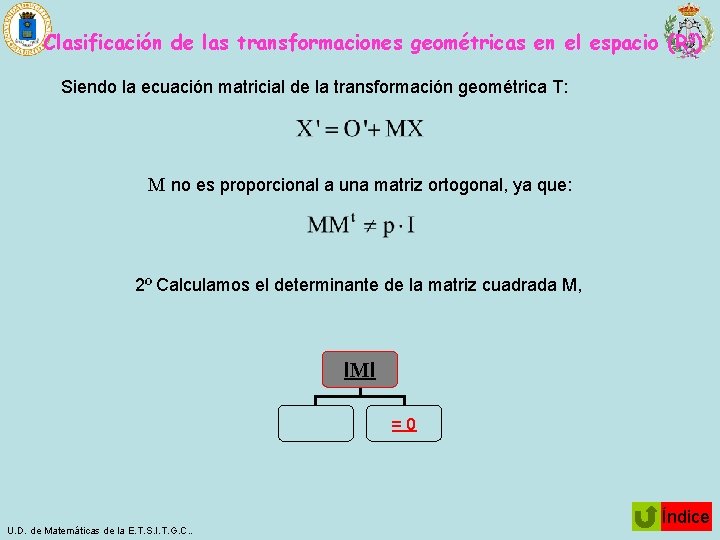
Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: M no es proporcional a una matriz ortogonal, ya que: 2º Calculamos el determinante de la matriz cuadrada M, IMI =0 U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: M no es proporcional a una matriz ortogonal, entonces T es una transformación afín, no es una semejanza, ni un movimiento. FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

Clasificación de las transformaciones geométricas en el espacio (R 3) Siendo la ecuación matricial de la transformación geométrica T: T no es biyectiva y por lo tanto no es una transformación geométrica. FIN U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice

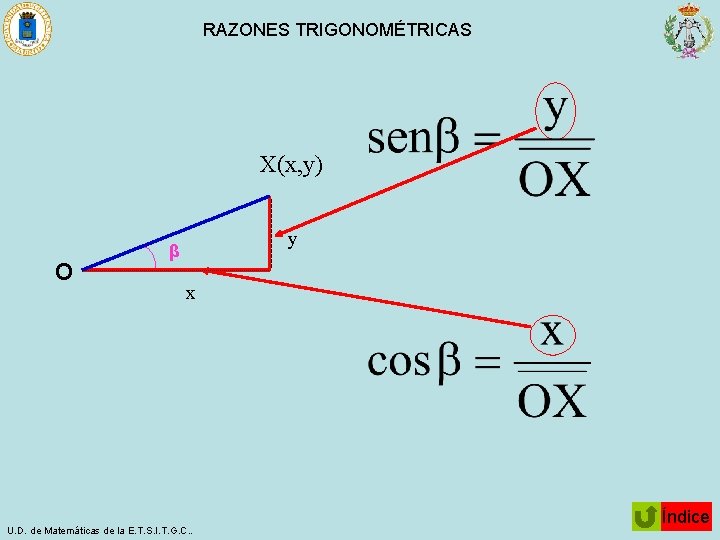
RAZONES TRIGONOMÉTRICAS X(x, y) O y β x U. D. de Matemáticas de la E. T. S. I. T. G. C. . Índice