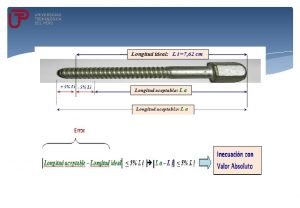
Inecuaciones con Valor Absoluto Propiedades para resolver inecuaciones

Inecuaciones con Valor Absoluto Propiedades para resolver inecuaciones con valor absoluto

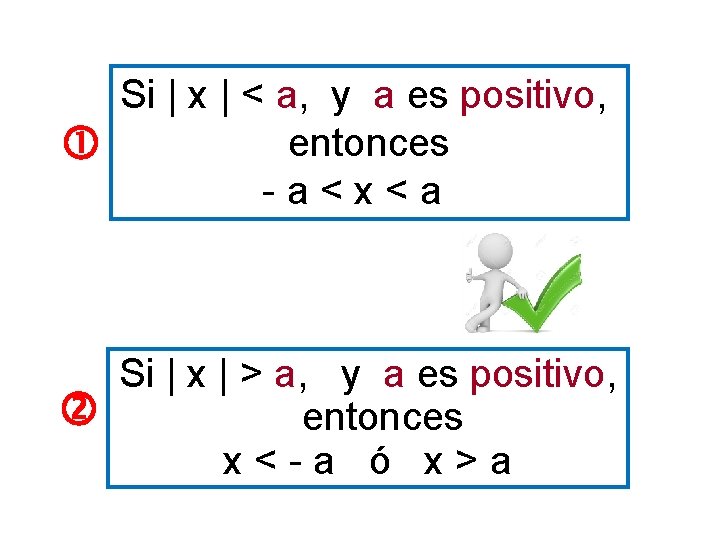
Si | x | < a, y a es positivo, entonces - a < x < a Si | x | > a, y a es positivo, entonces x < - a ó x > a

Ejemplo 1 v | x + 5 | ≤ 10 -10 ≤ x + 5 ≤ 10 -10 + - 5 ≤ x ≤ 10 + – 5 - 15 ≤ x ≤ 5 • La gráfica es: -15 -10 -5 0 5 10 15

Ejemplo 2 v | -3 x + 6 | > 18 -3 x + 6 < -18 ó -3 x + 6 > 18 -3 x < -24 -3 x > 12 x > 8 x < -4 • La gráfica es: -4 -2 0 2 4 6 8

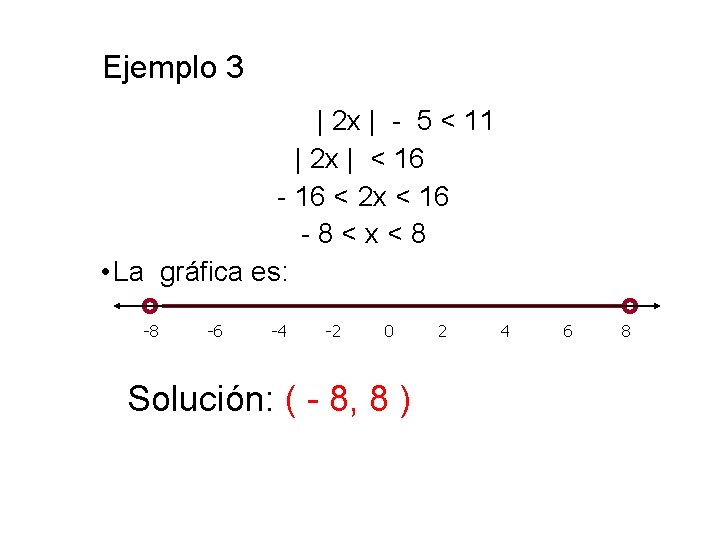
Ejemplo 3 | 2 x | - 5 < 11 | 2 x | < 16 - 16 < 2 x < 16 - 8 < x < 8 • La gráfica es: -8 -6 -4 -2 0 Solución: ( - 8, 8 ) 2 4 6 8

¿ Qué hacer si después de despejar se obtiene un número negativo? • Se resuelve por lógica , es decir, analizando la situación (no por cálculos, ni aplicando la propiedad) ¿Cuándo es un valor absoluto menor que un número negativo? NUNCA. Esto significa que no tiene solución. Ejemplo | x - 1 | – 5 • L a solución es ya que la función valor absoluto debe ser mayor o igual a cero ¿Cuándo es un valor absoluto mayor que un número negativo? SIEMPRE. Esto significa que la solución son todos los números Reales. | Ejemplo | x - 3 | ≥ – 2 • La solución son todos los números Reales ( - , + ) • La gráfica es toda la recta numérica