Graficacin IA 7200 T Transformaciones Geomtricas Transformaciones Geomtricas

Graficación IA 7200 -T Transformaciones Geométricas

Transformaciones Geométricas • Producto Matricial • Transformaciones Lineales • Rotaciones • Escalamiento • Acizallamiento • Translaciones Graficación • • • Coordenadas Homogéneas Transformaciones Inversas Rotaciones Arbitrarias Cambio de Coordenadas Rotaciones 3 D 2

Producto Matricial Graficación 3

Transformaciones Lineales Una transformación T es un mapeo Una transformación es lineal si para todos v y w (vectores) y λ (real) Si T es lineal: Graficación 4

Transformaciones Lineales En el espacio x-y, asociemos un punto P al vector V, tal que: T es un mapeo de puntos a puntos: Para todo punto P en x-y, donde: Graficación 5

Transformaciones Lineales Las TLs pueden ser escritas como un producto de matrices. Por ejemplo Se puede escribir como el producto Graficación 6

Transformaciones Lineales Ejemplo: 1. 2 1 Los renglones de T son las imágenes de (1, 0) y (0, 1) 0. 8 P 0. 6 Pt 0. 4 0. 2 0 0 Graficación 0. 5 1 1. 5 2 2. 5 7

Rotación Graficación 8

Escalamiento Graficación Sx=Sy=-1 Reflexión con respecto a O Sx=1, Sy=-1 Reflexión con respecto a X Sx=-1, Sy=1 Reflexión con respecto a Y 9

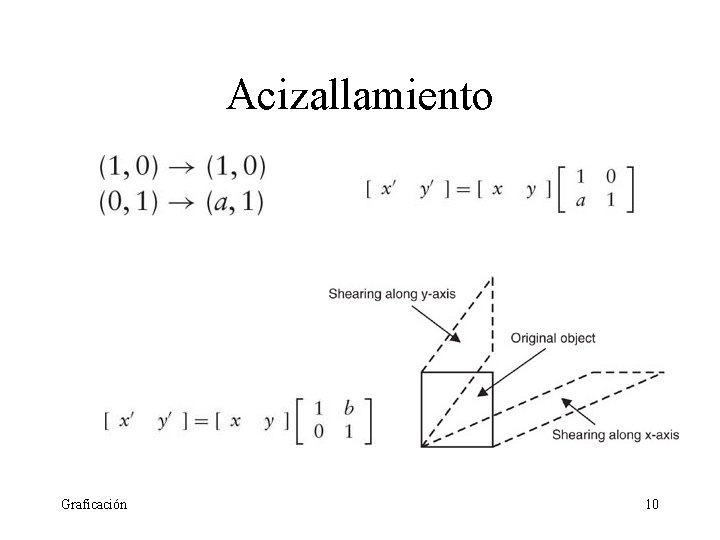
Acizallamiento Graficación 10

Translaciones ¿Cuál es la matriz T para translaciones? T no es lineal (i. e. T(0) = (a, b)≠ 0) (a, b) se llama vector de desplazamiento (shift vector) Graficación 11

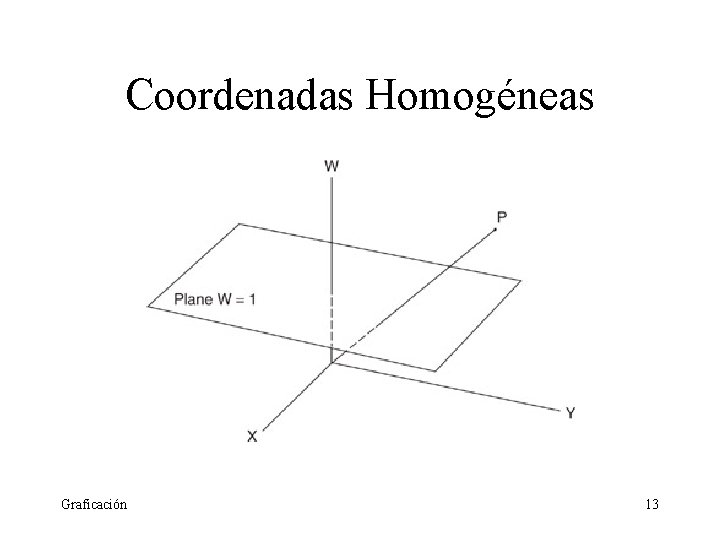
Coordenadas Homogéneas Para combinar todas las transfomaciones vistas hasta aquí, añadimos una dimensión mas, W. La dimensión extra hace que P=(x, y) tenga toda una familia de representaciones coordenadas (wx, wy, w) w≠ 0. Por ejemplo, (3, 6, 1), (0. 3, 0. 6, 0. 1), (6, 12, 2), (12, 24, 4), etc. Cuando un punto se mapea al plano W=1, se dice que está homogeneizado. Conversión: (x, y) (x, y, 1) (wx, wy, w) (wx/w, wy/w) Graficación 12

Coordenadas Homogéneas Graficación 13

Coordenadas Homogéneas T en coordenadas homogéneas Translación Rotación Graficación 14

Ejercicios • Dibuje un rectángulo unitario en un espacio R 2 • Genere una matriz T 1 para una rotación de 15° • Genere una matriz T 2 para un escalamiento de 1. 5 en x y 2 en y • Genere una matriz T 3 para un acizallamiento de 0. 5 en la horizontal • Combínelas, para formar una sola matriz T de transformación que además desplace el rectángulo por (1, 0. 5) • Aplique la matriz resultante al rectángulo Graficación 15

Ejercicios Ver Programa de Mathematica Graficación 16

Transformaciones Inversas • Si R mapea de P a P’, la inversa mapea de P’ a P. • Ej. Rotación Inversa • Se debe cumplir que Graficación 17

Transformaciones Inversas • Sin embargo, no todas las transformaciones son reversibles • Ej. Una transformación que mapea de cualquier punto al eje x no lo es. • La matriz no tiene inversa • Para que una matriz tenga inversa, su determinante debe ser diferente de cero Graficación 18

Transformaciones Inversas • La matriz de transformación del mapeo Graficación 19

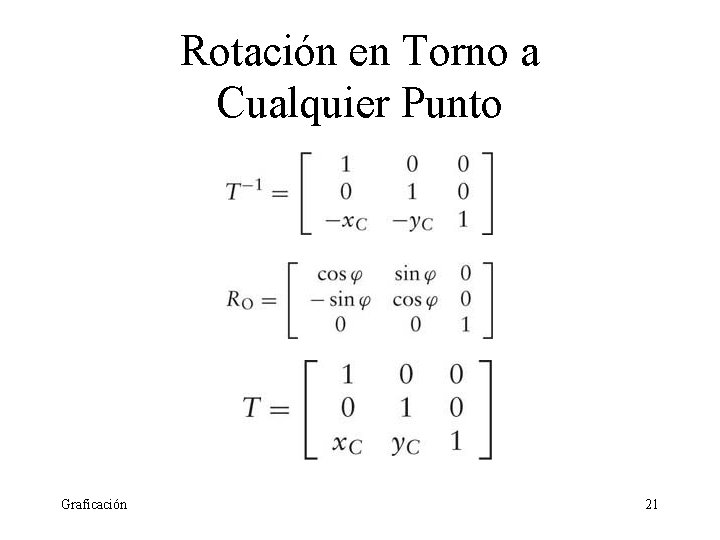
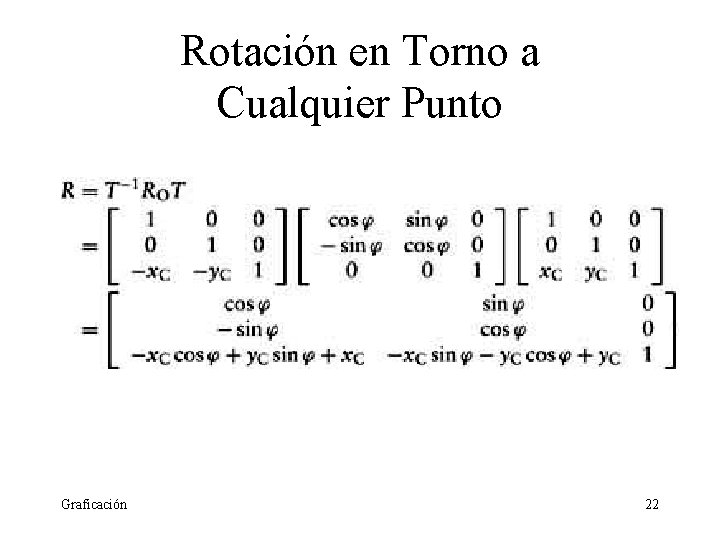
Rotación en Torno a Cualquier Punto • No es lineal • Puede ser descrita como un producto matricial (coordenadas homogéneas) • La rotación en el punto C(Xc, Yc) en un ángulo φ se puede hacer en tres pasos: • Translación al origen • Rotación en el origen • Translación de regreso Graficación 20

Rotación en Torno a Cualquier Punto Graficación 21

Rotación en Torno a Cualquier Punto Graficación 22

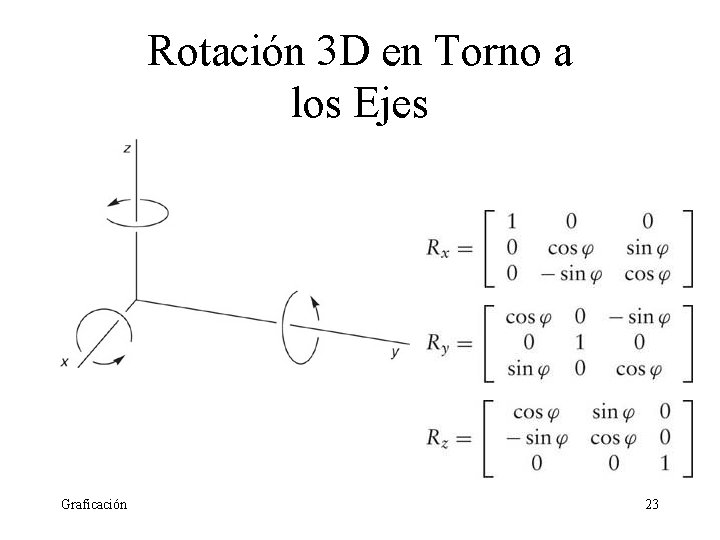
Rotación 3 D en Torno a los Ejes Graficación 23

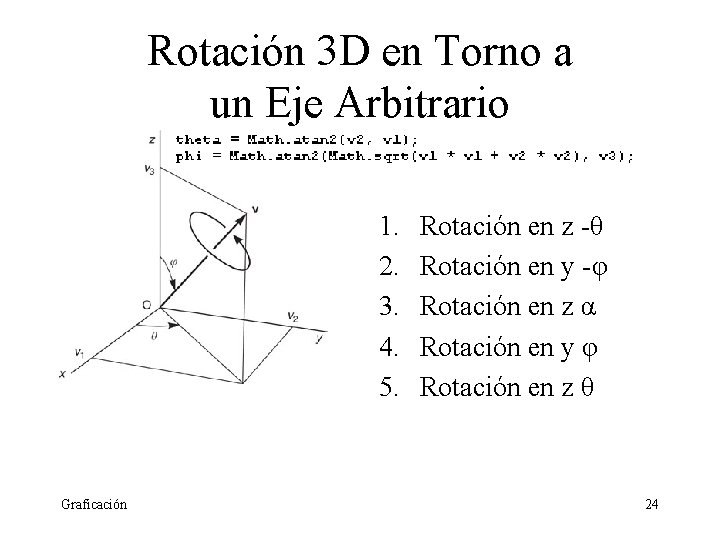
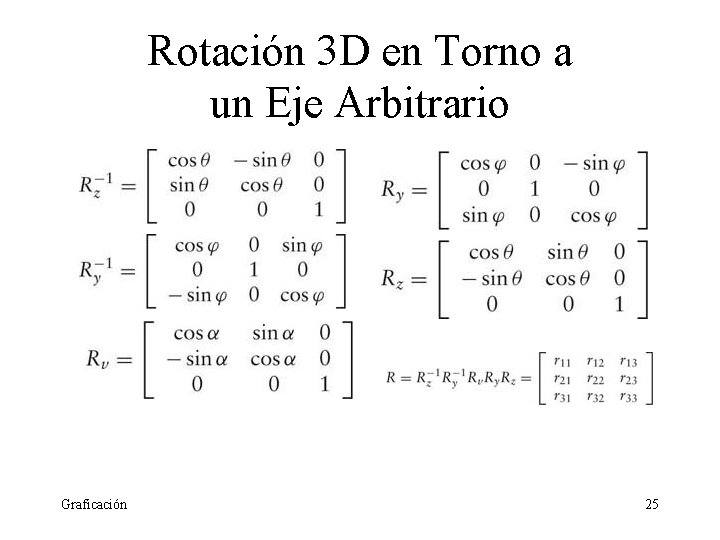
Rotación 3 D en Torno a un Eje Arbitrario 1. 2. 3. 4. 5. Graficación Rotación en z -θ Rotación en y -φ Rotación en z α Rotación en y φ Rotación en z θ 24

Rotación 3 D en Torno a un Eje Arbitrario Graficación 25

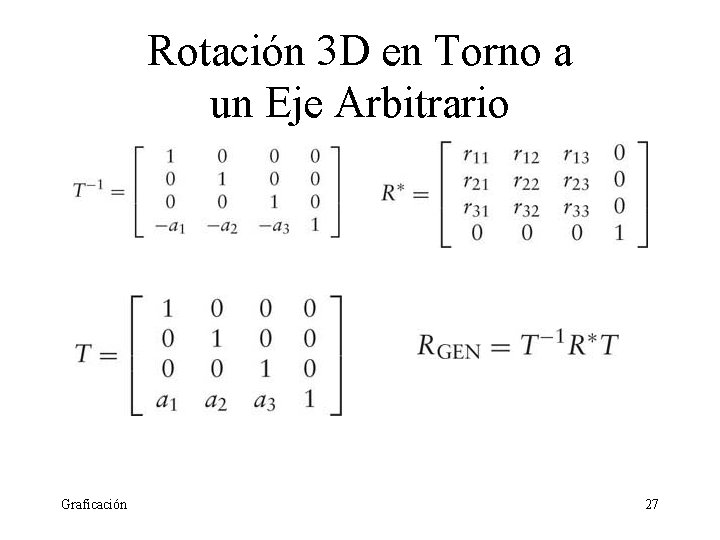
Rotación 3 D en Torno a un Eje Arbitrario Si el punto de inicio no es el origen, sino un punto arbitrario A(a 1, a 2, a 3) ① Translación de A a O ② La rotación R, descrita anteriormente ③ Translación inversa de O a A Graficación 26

Rotación 3 D en Torno a un Eje Arbitrario Graficación 27