TRANSFORMACIONES GEOMTRICAS GRAFICACIN I Transformaciones en dos dimensiones

TRANSFORMACIONES GEOMÉTRICAS GRAFICACIÓN I

Transformaciones en dos dimensiones Los objetos se definen mediante un conjunto de puntos. Las transformaciones son procedimientos para calcular nuevas posiciones de estos puntos, cambiado el tamaño y orientación del objeto. Las operaciones básicas de transformación son q Traslación q Escalamiento q Rotación.

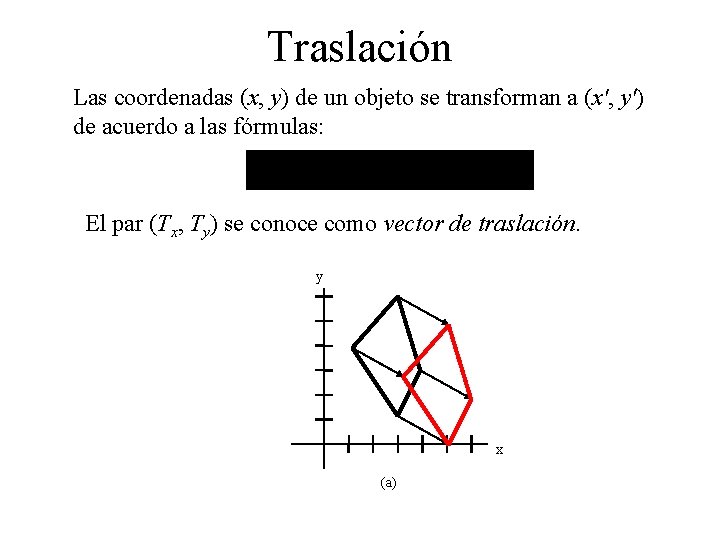
Traslación Las coordenadas (x, y) de un objeto se transforman a (x', y') de acuerdo a las fórmulas: El par (Tx, Ty) se conoce como vector de traslación. y x (a)

Ejemplo traslación Vector de desplazamiento T = (– 3, – 2) (x 1, y 1) = (2, 3) (x 2, y 2) = (1, 1) (x 3, y 3) = (3, 1) (x 1’, y 1’) = (2, 3) + (– 3, – 2) = (– 1, 1) (x 2’, y 2’) = (1, 1) + (– 3, – 2) = (– 2, – 1) (x 3’, y 3’) = (3, 1) + (– 3, – 2) = (0, – 1) (x 1, y 1) Vector de desplazamiento (x 1’, y 1’) (x 2’, y 2’) (x 2, y 2) (x 3’, y 3’) (x 3, y 3)

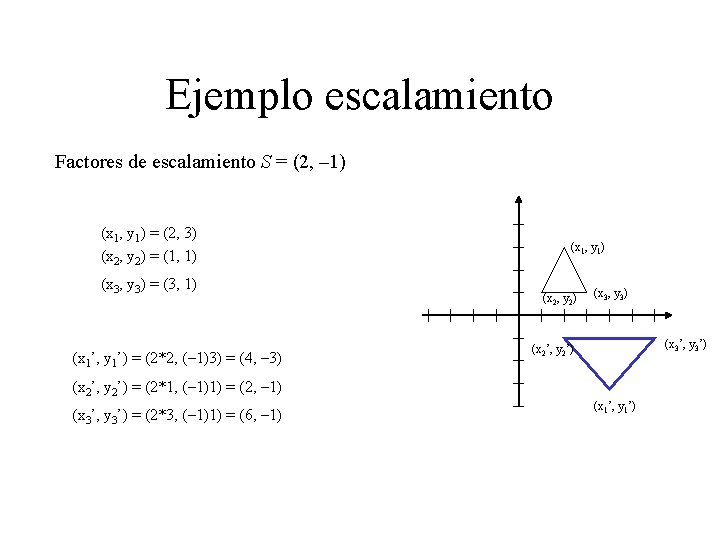
Escalamiento El escalamiento modifica el tamaño de un polígono. Para obtener este efecto, se multiplica cada par coordenado (x, y) por un factor de escala en la dirección x y en la dirección y para obtener el par (x', y'). Las fórmulas son

Ejemplo escalamiento Factores de escalamiento S = (2, – 1) (x 1, y 1) = (2, 3) (x 2, y 2) = (1, 1) (x 3, y 3) = (3, 1) (x 1’, y 1’) = (2*2, (– 1)3) = (4, – 3) (x 1, y 1) (x 2, y 2) (x 3, y 3) (x 3’, y 3’) (x 2’, y 2’) = (2*1, (– 1)1) = (2, – 1) (x 3’, y 3’) = (2*3, (– 1)1) = (6, – 1) (x 1’, y 1’)

Rotación La rotación gira los puntos de una figura alrededor de un punto fijo. De la figura se obtiene Simplificando

Ejemplo rotación Ángulo de rotación q = 45° (x 1, y 1) = (2, 3) (x 1’, y 1’) (x 3’, y 3’) (x 1, y 1) (x 2, y 2) = (1, 1) (x 3, y 3) = (3, 1) (x 1’, y 1’) = (2 cos(45°) – 3 sen(45°), 3 cos(45°) + 2 sen(45°)) = (2*0. 707– 3*0. 707, 3*0. 707+2*0. 707) = (– 0. 707, 3, 54) (x 2’, y 2’) = (3 cos(45°) –sen(45°), cos(45°) + 3 sen(45°)) = (3*0. 707– 0. 707, 0. 707+3*0. 707) = (1. 414, 2. 828) (x 3’, y 3’) = (cos(45°) – sen(45°), cos(45°) + sen(45°)) = (0. 707– 0. 707, 0. 707+0. 707) = (0, 1. 414) (x 2’, y 2’) (x 2, y 2) (x 3, y 3)

Escalamiento respecto a un punto fijo Se puede llevar a cabo un escalamiento respecto a un punto fijo trasladando primero ese punto al origen, después escalando y luego regresando el objeto a la posición original. Las ecuaciones son Reacomodando

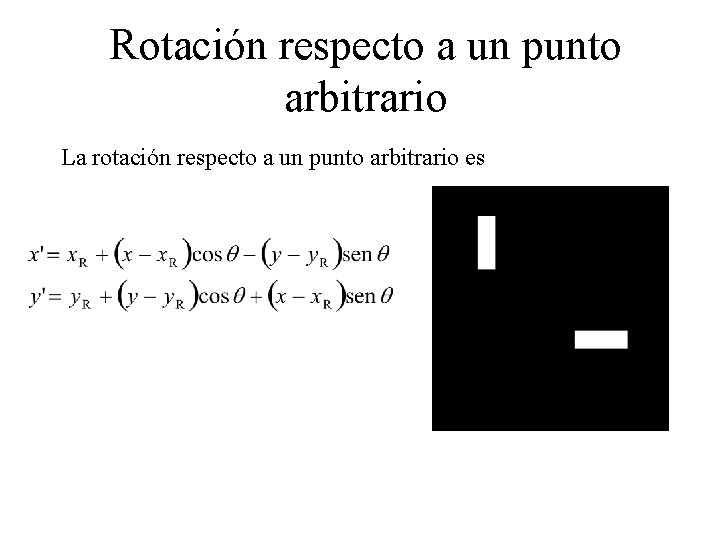
Rotación respecto a un punto arbitrario La rotación respecto a un punto arbitrario es

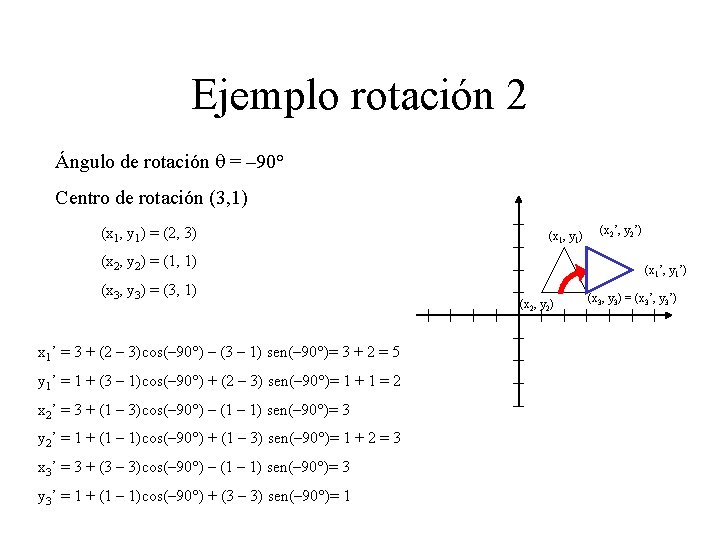
Ejemplo rotación 2 Ángulo de rotación q = – 90° Centro de rotación (3, 1) (x 1, y 1) = (2, 3) (x 1, y 1) (x 2, y 2) = (1, 1) (x 3, y 3) = (3, 1) x 1’ = 3 + (2 – 3)cos(– 90°) – (3 – 1) sen(– 90°)= 3 + 2 = 5 y 1’ = 1 + (3 – 1)cos(– 90°) + (2 – 3) sen(– 90°)= 1 + 1 = 2 x 2’ = 3 + (1 – 3)cos(– 90°) – (1 – 1) sen(– 90°)= 3 y 2’ = 1 + (1 – 1)cos(– 90°) + (1 – 3) sen(– 90°)= 1 + 2 = 3 x 3’ = 3 + (3 – 3)cos(– 90°) – (1 – 1) sen(– 90°)= 3 y 3’ = 1 + (1 – 1)cos(– 90°) + (3 – 3) sen(– 90°)= 1 (x 2’, y 2’) (x 1’, y 1’) (x 2, y 2) (x 3, y 3) = (x 3’, y 3’)

Código en C struct point{ float x, y; }; void translate(point &p, float tx, float ty){ p. x = p. x + tx; p. y = p. y + ty; } void scale(point &p, float sx, float sy){ p. x = sx*p. x; p. y = sy*p. y; } void rotate(point &p, float a){ float sn = sin(a*PI/180); float cs = cos(a*PI/180); p. x = cs*p. x - sn*p. y; p. y = cs*p. y + sn*p. x; }

void rotate. Fix(point &p, float a, float xr, float yr){ translate(p, -xr, -yr); rotate(p, a); translate(p, xr, yr); } void scale. Fix(point &p, float sx, float sy, float xf, float yf){ translate(p, -xf, -yf); scale(p, sx, sy); translate(p, xf, yf); } void translate. Poly(point *p, int n, float tx, float ty){ for(int i=0; i<n ; i++) translate(p[i], tx, ty); }

Tarea Escriba una función que dibuje un polígono relleno. Haciendo uso de esa función, escriba un programa en C que dibuje la figura que se muestra transformada mediante traslaciones, escalamientos y rotaciones para crear la imagen que se muestra.

Coordenadas homogéneas Para poder representar las tres transformaciones en forma matricial como producto de matrices, es necesario representar los puntos en coordenadas homogéneas. Estas coordenadas agregan una tercer componente a las coordenadas bidimensionales. De tal forma que, un punto (x, y) pasa a ser (x, y, W). El punto en coordenadas Cartesianas representado por esta tríada es el (x/W, y/W). El valor de W es generalmente 1.

Representación matricial de traslaciones Haciendo uso de coordenadas homogéneas la traslación puede representarse como: En forma abreviada la transformación se representará por T(Tx, Ty)

Representación matricial de escalamientos Haciendo uso de coordenadas homogéneas el escalamiento puede representarse como: En forma abreviada la transformación se representará por S(Sx, Sy)

Representación matricial de rotaciones Haciendo uso de coordenadas homogéneas la rotación puede representarse como: En forma abreviada la transformación se representará por R(q)

Composición de transformaciones Para aplicar varias transformaciones a un conjunto de puntos basta con combinar las matrices de transformación en una sola, mediante multiplicación matricial. En caso de tener solo transformaciones del mismo tipo, la combinación sigue reglas muy simples. Traslación: Escalamiento: Rotación:

Escalamiento respecto a un punto fijo en forma matricial Para llevar a cabo un escalamiento respecto a un punto fijo, se procede multiplicando una matriz de traslación para llevar el punto fijo al origen por una de escalamiento y posteriormente por otra de traslación para llevar al punto fijo a su posición original.

Rotación respecto a un punto fijo en forma matricial Para llavar a cabo una rotación respecto a un punto fijo, se procede multiplicando una matriz de traslación para llevar el punto fijo al origen por una de rotación y posteriormente por otra de traslación para llevar al punto fijo a su posición original.

Forma general En general una transformación que utilice traslaciones, escalamientos y rotaciones tendrá la forma: Por tanto, el cálculo de las coordenadas transformadas se podrá hacer con las siguientes ecuaciones

Otras transformaciones que permiten llevar a cabo operaciones muy útiles, estas son: q Reflexiones q Corte.

Reflexiones en x y y Las reflexiones respecto al eje x y y se obtienen con las matrices siguientes:

Reflexión respecto al origen La reflexión respecto al origen se obtiene con :

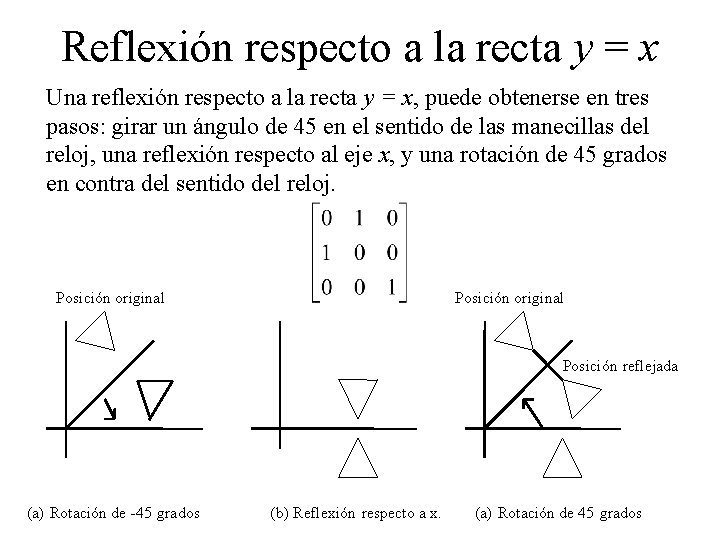
Reflexión respecto a la recta y = x Una reflexión respecto a la recta y = x, puede obtenerse en tres pasos: girar un ángulo de 45 en el sentido de las manecillas del reloj, una reflexión respecto al eje x, y una rotación de 45 grados en contra del sentido del reloj. Posición original Posición reflejada (a) Rotación de -45 grados (b) Reflexión respecto a x. (a) Rotación de 45 grados

Corte en x El corte produce una deformación similar al deslizamiento de una capa sobre otra. El corte en x se produce por la matriz:

Corte en y El corte en y se produce por la matriz

Implementación de transformaciones con matrices Para la implementación de matrices es conveniente definir tipos para punto y matriz. Luego funciones para crear las matrices de las transformaciones básicas. Lo primero es crear una matriz unitaria y a partir de está crear las demás funciones. Es necesaria definir una función para multiplicar matrices y poder acumular las transformaciones. Otra función debe aplicar una matriz de transformación a un punto y regresar el punto transformado. Finalmente aplicar la matriz a un ppolígono.

Tipos básicos Los tipos básicos para punto, matriz y polígono son los siguientes: typedef double Point[3]; typedef double Matrix[3][3]; typedef Point poligono[10]; El punto p(1, -4) se define como Point p = {1, -4, 1};

Crear matriz identidad La matriz identidad es la base para las demás funciones void set_identity(Matrix m){ int i, j; for(i = 0; i<3 ; i++) for(j = 0; j<3 ; j++) m[i][j] = (i==j); }

Matrices de traslación y escalamiento Matriz de traslación. void create_traslation_matrix(double tx, double ty, Matrix t){ set_identity(t); t[2][0] = tx; t[2][1] = ty; } Matriz de escalamiento: void create_scale_matrix(double sx, double sy, Matrix t){ set_identity(t); t[0][0] = sx; t[1][1] = sy; }

Matriz de rotación El ángulo se especifica en grados. void create_rotation_matrix(double a, Matrix t){ set_identity(t); double sn = sin(a*PI/180); double cs = cos(a*PI/180); t[0][0] = cs; t[0][1] = sn; t[1][0] = -sn; t[1][1] = cs; }

Matriz de corte Solo es necesario definir una matriz de corte. Si se hace solo corte en x, shy = 0 y si se hace solo corte en y, shx = 0. void create_shear_matrix(double shx, double shy, Matrix t){ set_identity(t); t[0][1] = shy; t[1][0] = shx; }

Acumula dos transformaciones Los parámetros m 1 y m 2 son de entrada, el resultado se almacena en m. void accumulate_matrices(Matrix m 1, Matrix m 2, Matrix m){ int i, j, k; double s; for(i = 0; i<3 ; i++) for(j = 0; j<3 ; j++){ s = 0; for(k = 0; k<3 ; k++) s = s+m 1[i][k]*m 2[k][j]; m[i][j] = s; } }

Transformar un punto y un polígono El punto de entrada es p 1 y el de salida p 2. void transform. Point(Point p 1, Matrix m, Point p 2){ p 2[0] = m[0][0]*p 1[0]+m[1][0]*p 1[1]+m[2][0]*p 1[2]; p 2[1] = m[0][1]*p 1[0]+m[1][1]*p 1[1]+m[2][1]*p 1[2]; p 2[2] = m[0][2]*p 1[0]+m[1][2]*p 1[1]+m[2][2]*p 1[2]; } El polígono de entrada es p 1 y el de salida p 2. n es el número de puntos del polígono. void transform. Poly(poligono p 1, int n, Matrix m, poligono p 2){ for(int i = 0; i<n; i++) transform. Point(p 1[i], m, p 2[i]); }

Dibujar polígono Dibuja un polígono. Note que la tercer coordenada no se usa. void draw(poligono p, int n){ moveto((int)p[0][0], (int)p[0][1]); for(int i=1; i<n; i++){ lineto((int)p[i][0], (int)p[i][1]); } }

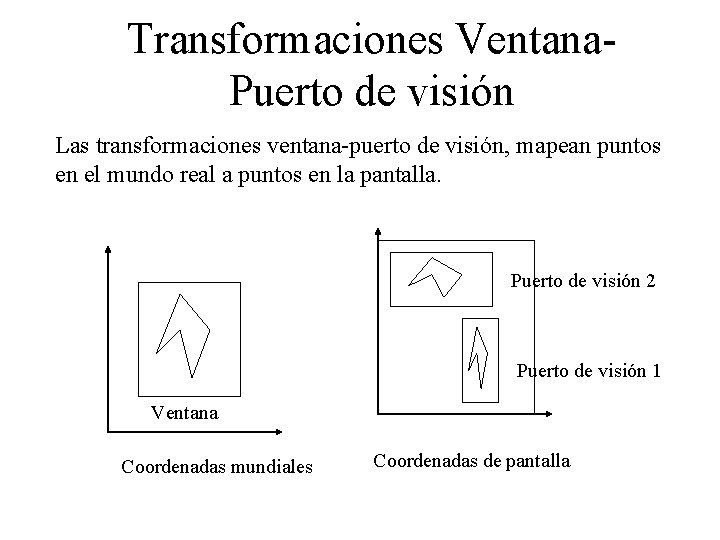
Transformaciones Ventana. Puerto de visión Las transformaciones ventana-puerto de visión, mapean puntos en el mundo real a puntos en la pantalla. Puerto de visión 2 Puerto de visión 1 Ventana Coordenadas mundiales Coordenadas de pantalla

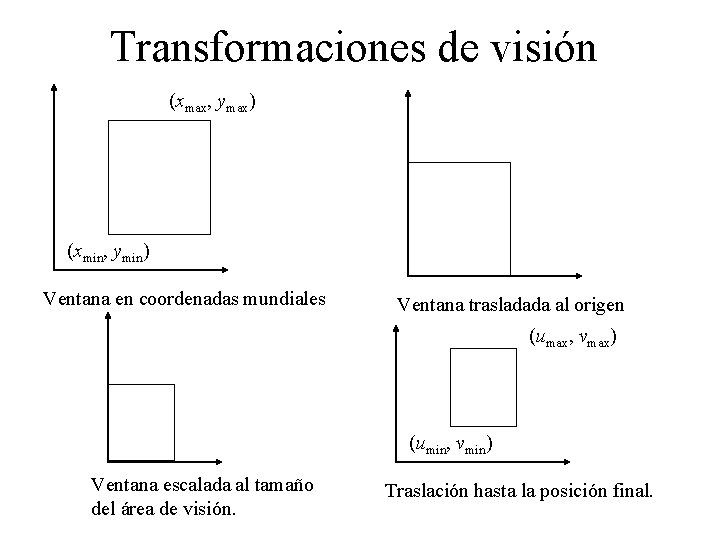
Transformaciones de visión (xmax, ymax) (xmin, ymin) Ventana en coordenadas mundiales Ventana trasladada al origen (umax, vmax) (umin, vmin) Ventana escalada al tamaño del área de visión. Traslación hasta la posición final.

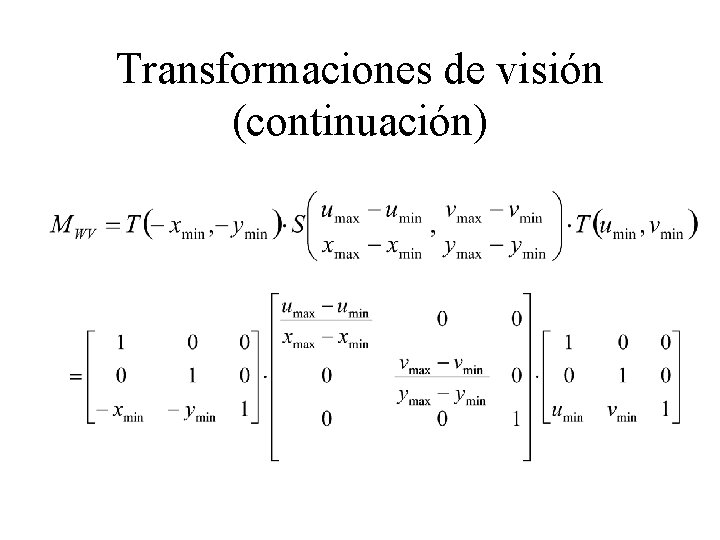
Transformaciones de visión (continuación)

Transformaciones de visión (continuación)

Implementación en C void crate_window_view_matrix( double xmin, double ymin, double xmax, double ymax, int umin, int vmin, int umax, int vmax, Matrix m){ Matrix m 1, m 2, m 3, m 4; create_traslation_matrix(-xmin, -ymin, m 1); create_scale_matrix((umax-umin)/(xmax-xmin), (vmax-vmin)/(ymax-ymin), m 2); create_traslation_matrix(umin, vmin, m 3); accumulate_matrices(m 1, m 2, m 4); accumulate_matrices(m 4, m 3, m); }

Rutina de despliegue void show_polygon( double xmin, double ymin, double xmax, double ymax, int umin, int vmin, int umax, int vmax, poligono p){ Matrix m 1, m 2; poligono p 2, p 3; //poligonos transformados int xv 1, xv 2, yv 1, yv 2; //coordenadas del viewport //es necesario ordenar las coordenadaas del viewport if(umin>umax){ xv 1 = umax; xv 2 = umin; }else{ xv 1 = umin; xv 2 = umax; } if(vmin>vmax){ yv 1 = vmax; yv 2 = vmin; }else{ yv 1 = vmin; yv 2 = vmax; }

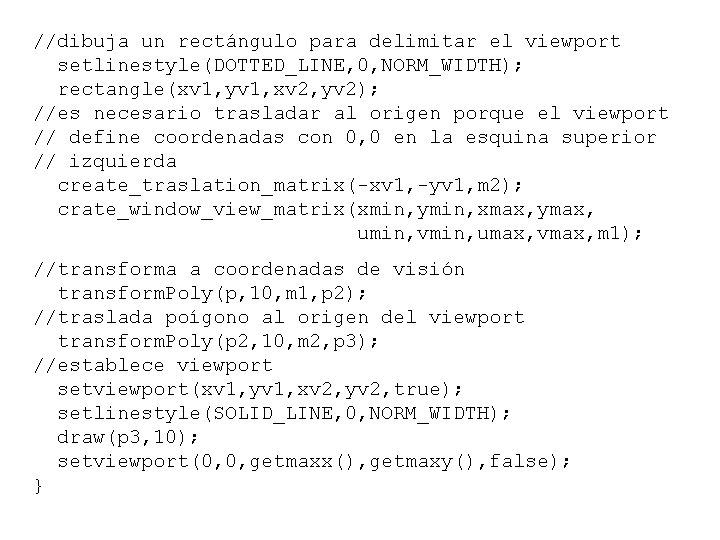
//dibuja un rectángulo para delimitar el viewport setlinestyle(DOTTED_LINE, 0, NORM_WIDTH); rectangle(xv 1, yv 1, xv 2, yv 2); //es necesario trasladar al origen porque el viewport // define coordenadas con 0, 0 en la esquina superior // izquierda create_traslation_matrix(-xv 1, -yv 1, m 2); crate_window_view_matrix(xmin, ymin, xmax, ymax, umin, vmin, umax, vmax, m 1); //transforma a coordenadas de visión transform. Poly(p, 10, m 1, p 2); //traslada poígono al origen del viewport transform. Poly(p 2, 10, m 2, p 3); //establece viewport setviewport(xv 1, yv 1, xv 2, yv 2, true); setlinestyle(SOLID_LINE, 0, NORM_WIDTH); draw(p 3, 10); setviewport(0, 0, getmaxx(), getmaxy(), false); }

Ejemplo de función main(){ poligono p, p 2; Matrix m 1, m 2; init. Pol(p); initwindow(500, 500); show_polygon(5, 5, 20, 220, 350, 450, 20, p); show_polygon(-1, 11, 20, 100, 20, p); show_polygon(-10, 20, 20, 200, 120, p); show_polygon(-1, 5, 5, 20, 370, 140, 250, p); getch(); }

Salida del ejemplo

Propiedades de las transformaciones Los vectores fila de la submatriz superior 2 x 2 de rotación tienen tres propiedades: 1. Cada uno es un vector unidad 2. Cada uno es perpendicular al otro (su producto punto es cero) 3. El primer y segundo vector se rotarán por R(q) para que caigan sobre los ejes x y y positivos. 4. Una matriz que cumple esto se le llama ortogonal especial.

Una matriz de transformación de la forma: Donde la submatriz superior de 2 x 2 es ortogonal, conserva los ángulos y las longitudes. Estas transformaciones se denominan de cuerpo rígido. Una secuencia arbitraria de traslaciones, rotaciones y escalamientos conserva el paralelismo de las líneas, pero no la longitud ni los ángulos. Estas transformaciones se denominan transformaciones afines.

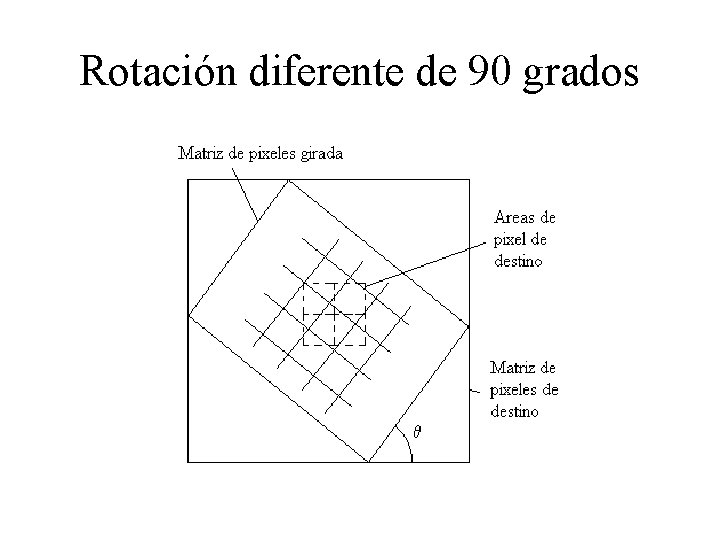
Operaciones de rastreo El buffer de pantalla se puede manipular directamente para llevar a cabo algunas transformaciones. La más sencilla es la copia de un bloque de un lugar de la pantalla a otro. Para girar una figura un ángulo múltiplo de 90 grados se pueden lograr invirtiendo renglones por columnas. La rotación por 180 grados se logra invirtiendo cada renglón y posteriormente invirtiendo los renglones. Para otros ángulos cada área de pixel de destino se diagrama sobre la matriz que se gira y se calcula la cantidad de superposición con las áreas de pixel que se giran. Entonces se calcula una intensidad para el pixel al promediar las intensidades de los pixeles fuente superpuestos.

Rotación diferente de 90 grados

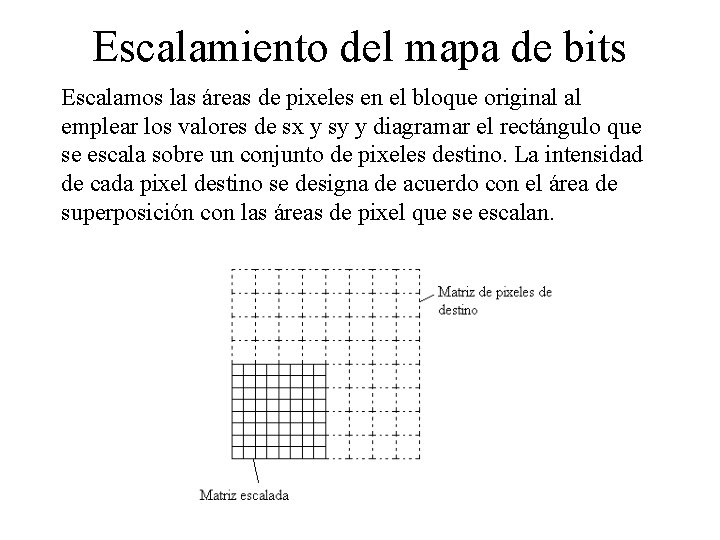
Escalamiento del mapa de bits Escalamos las áreas de pixeles en el bloque original al emplear los valores de sx y sy y diagramar el rectángulo que se escala sobre un conjunto de pixeles destino. La intensidad de cada pixel destino se designa de acuerdo con el área de superposición con las áreas de pixel que se escalan.

Tarea Escribir una biblioteca para realizar transformaciones de 2 D utilizando matrices, defina lo siguiente: - Tipo vector y tipo matriz en coordenadas homogéneas - Rutinas para: trasladar, rotar, escalar, reflejar, cortar y transformación de puerto de visión.

Animación Para lograr una animación mediante transformaciones es conveniente mantener una copia del los objetos sin transformar. Para lograr la animación se copia el objeto original, luego se le aplican a esta copia las transformaciones a realizar y se dibuja el objeto transformado. -Copiar objeto - transformar - dibujar

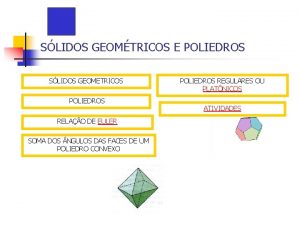
Ejemplo Define un cruz: void init(){ poly[0]. x = 0; poly[0]. y = 10; poly[1]. x = 10; poly[1]. y = 10; poly[2]. x = 10; poly[2]. y = 0; poly[3]. x = 20; poly[3]. y = 0; poly[4]. x = 20; poly[4]. y = 10; poly[5]. x = 30; poly[5]. y = 10; poly[6]. x = 30; poly[6]. y = 20; poly[7]. x = 20; poly[7]. y = 20; poly[8]. x = 20; poly[8]. y = 30; poly[9]. x = 10; poly[9]. y = 30; poly[10]. x = 10; poly[10]. y = 20; poly[11]. x = 0; poly[11]. y = 20; }

void play(){ while(true){ char c; if(kbhit()){ int i, p=0; c = (char)getch(); unsigned int size; switch(c){ point p 1[20]; case 27: return; float a=0, da = 0, vx=0, vy=0, x=0, y=0; case 'i': vy--; break; setactivepage(1); case 'm': vy++; break; for(i = 0; i< 1000; i++){ putpixel(rand()%400, rand()%15+1); case 'j': vx--; break; case 'k': vx++; break; } case 'r': da--; break; size = imagesize(0, 0, 400); case 't': da++; break; /* allocate memory to hold the image */ case ‘e': s--; break; img = malloc(size); case ‘w': s++; break; /* grab the image */ } getimage(0, 0, 400, img); } x += vx; y += vy; a += da; inicia Lee teclado a=(a>360)? a-360: a; a=(a<-360)? a+360: a; if(x>400) x= 0; if(y>400) y= 0; if(x<0) x= 400; if(y<0) y= 400;

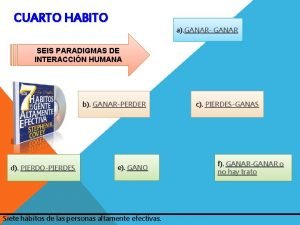
//copia el polígono orignal for(i = 0; i<12 ; i++) p 1[i] = poly[i]; setfillstyle(1, BLUE); setcolor(BLUE); Objeto original rotate. Poly(p 1, 12, a, 15); scale. Poly(p 1, 12, 3+s); Gira a grados translate. Poly(p 1, 12, x, y); setvisualpage(1 -p); Se escala 3+s veces setactivepage(p); putimage(0, 0, img, COPY_PUT); Traslada a x, y fill. Poly(p 1, 12); delay(10); swapbuffers( ); p = 1 -p; } Doble búfer para animar

Biblioteca de transformaciones //archivo: transform. h struct point{ float x, y; }; void translate(point &p, float tx, float ty); void scale(point &p, float sx, float sy); void rotate(point &p, float a); void rotate. Fix(point &p, float a, float xr, float yr); void scale. Fix(point &p, float sx, float sy, float xf, float yf); void translate. Poly(point *p, int n, float tx, float ty); void dibuja. Punto(point p); void dibuja. Poly(point *p, int n); void trans. W 2 V(point *p, int n, float xmin, float ymin, float xmax, float ymax, int umin, int vmin, int umax, int vmax); void copia(point *p 1, point *p 2, int n);

//archivo: transform. cpp #include <graphics. h> #include <math. h> #include "transform. h" float PI = 3. 14159265; void translate(point &p, float tx, float ty){. . . void trans. W 2 V(point *p, int n, float xmin, float ymin, float xmax, float ymax, int umin, int vmin, int umax, int vmax){ int i; for(i=0; i<n ; i++){ translate(p[i], -xmin, -ymin); scale(p[i], (umax-umin)/(xmax-xmin), (vmax-vmin)/(ymax-ymin)); translate(p[i], umin, vmin); } rectangle(umin, vmin, umax, vmax); } void copia(point *p 1, point *p 2, int n){ int i; for(i=0; i<n; i++) p 2[i] = p 1[i]; }

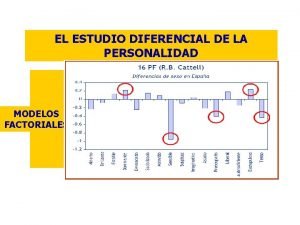
#include <graphics. h> #include "transform. h" main(){ initwindow(400, 400); point p[10], p 1[10]; p[0]. x = 0; p[0]. y = 10; p[1]. x = 10; p[1]. y = 10; p[2]. x = 10; p[2]. y = 0; p[3]. x = 20; p[3]. y = 0; p[4]. x = 20; p[4]. y = 10; p[5]. x = 30; p[5]. y = 10; dibuja. Poly(p, 6); copia(p, p 1, 6); trans. W 2 V(p 1, 6, 0, 0, 30, 100, 150); dibuja. Poly(p 1, 6); copia(p, p 1, 6); trans. W 2 V(p 1, 6, 0, 0, 30, 200, 100, 350, 300); dibuja. Poly(p 1, 6); // setviewport(100, 200, true); // dibuja. Poly(p, 6); getch(); }