SLIDOS GEOMTRICOS E POLIEDROS SLIDOS GEOMETRICOS POLIEDROS RELAO

SÓLIDOS GEOMÉTRICOS E POLIEDROS SÓLIDOS GEOMETRICOS POLIEDROS RELAÇÃO DE EULER SOMA DOS NGULOS DAS FACES DE UM POLIEDRO CONVEXO POLIEDROS REGULARES OU PLATÔNICOS ATIVIDADES

SÓLIDOS GEOMÉTRICOS Introdução Grande parte dos objetos que nos são familiares tem formas geométricas definidas; são denominados sólidos geométricos. São objetos que lembram sólidos geométricos:

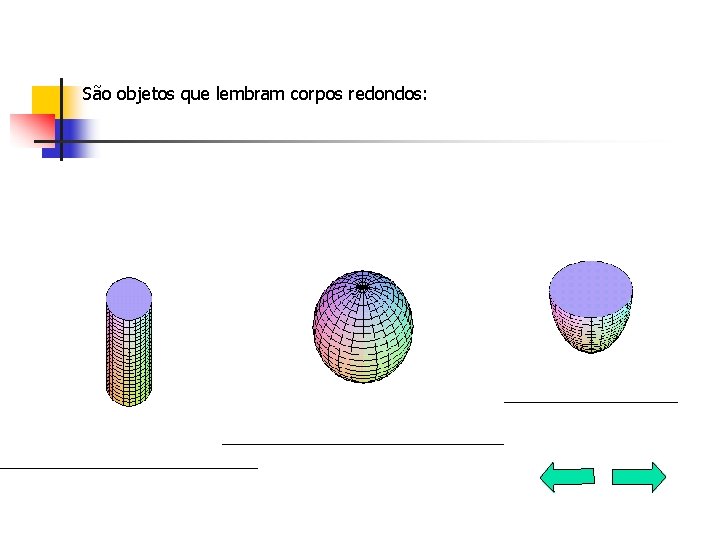
São objetos que lembram corpos redondos:

POLIEDRO Denomina-se Poliedros o sólido geométrico limitado por polígonos planos que têm, dois a dois, um lado comum. Elementos de um poliedro: Vértice Face Aresta Face: Região poligonal que limita o poliedro. Aresta: Interseção de duas faces. Vértice: Interseção de 3 ou mais arestas. Obs: Um poliedro possui no mínimo 4 faces.

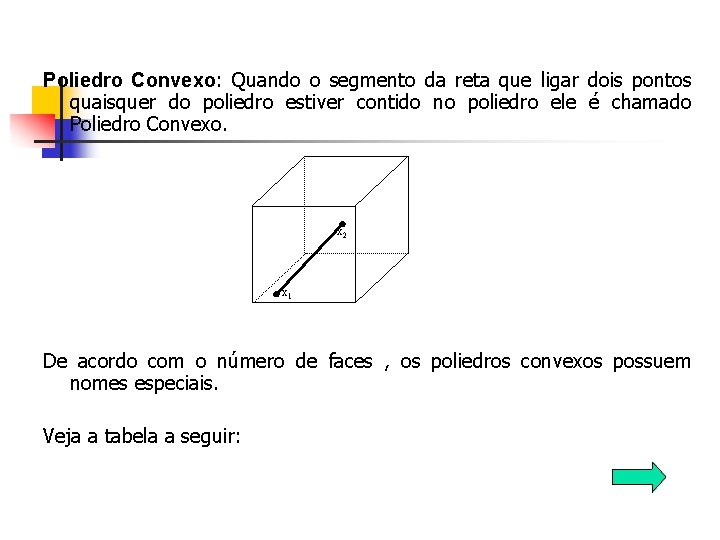
Poliedro Convexo: Quando o segmento da reta que ligar dois pontos quaisquer do poliedro estiver contido no poliedro ele é chamado Poliedro Convexo. x 2 x 1 De acordo com o número de faces , os poliedros convexos possuem nomes especiais. Veja a tabela a seguir:

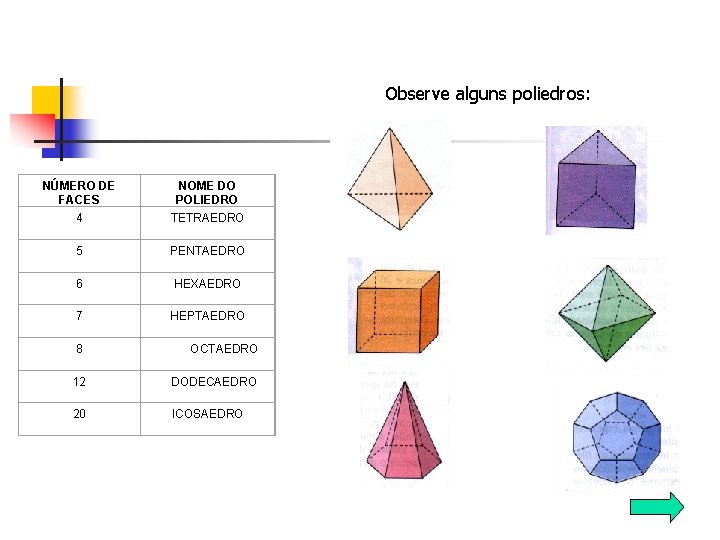
Observe alguns poliedros: NÚMERO DE FACES NOME DO POLIEDRO 4 TETRAEDRO 5 PENTAEDRO 6 HEXAEDRO 7 HEPTAEDRO 8 OCTAEDRO 12 DODECAEDRO 20 ICOSAEDRO

Poliedro Não- Convexo: Observe a figura abaixo: x 1 x 2 Nela vemos que existem pontos X 1 e X 2 do poliedro tais que o segmento de reta X 1 X 2 não está contido no poliedro, ou seja, uma parte do segmento “esta fora” do poliedro. De acordo com o seu n. de faces um poliedro pode ser classificado em Tetraedro(4 faces), Pentaedro(5 faces), Hexaedro(6 faces) e assim por diante. A relação que veremos a seguir estabelece correspondência entre o número de vértices, o número de arestas e o número de faces de um poliedro convexo.

Fórmula de Euler O autor desta façanha é Leonardo Euler (lê-se Óiler), grande matemático suíço (1707 - 1783), que produziu trabalhos em diversos ramos da ciência, como física, astronomia, biologia, matemática etc. Tinha uma memória inigualável e uma incrível destreza com a matemática. Euler escrevia seus trabalhos com a mesma facilidade com que um escritor redige uma carta. Nem a cegueira total que o afligiu durante os últimos dezessete anos de vida modificou isso; parece até que a cegueira o ajudou a desvendar mais ainda o seu mundo interior. Em qualquer poliedro convexo vale a seguinte relação: V-A+F = 2 Onde V= nº de vértices A= nº de arestas F= nº de faces Faremos apenas a verificação dessa relação através de um exemplo, no qual contaremos os vértices, as arestas e as faces de um poliedro. V=8 F =6 A = 12 V – A + F = 2 8 – 12 + 6 = 2

SOMA DOS NGULOS DAS FACES Soma dos ngulos das Faces A soma dos ângulos de todas as faces de um poliedro convexo é: S = (V-2). 360º onde V é o número de vértices. Demonstração: V, A e F são nesta ordem o número de vértices, arestas e faces do poliedro. Sejam n 1, n 2, n 3, . . . , n. F os números de lados das faces 1, 2, 3, . . . , F, ordenadamente. A soma dos ângulos de uma face é (n-2). 180º Para toda as faces temos: S = (n 1 -2). 180º + (n 2 -2). 180º + (n 3 -2). 180º +. . . + (n. F-2). 180º S = n 1180º - 360º + n 2180º - 360º + n 3180º - 360º +. . . + n. F 180º - 360º S = (n 1 + n 2 + n 3 +. . . +n. F). 180º - F. 360º mas n 1 + n 2 + n 3 +. . . +n. F = 2 A, logo S = 2 A. 180º - F. 360º S = 360º. A – F. 360º S = (A – F). 360º Da relação de Euler, temos V-A+F = 2 V-2 = A – F S = (V – 2). 360º

Poliedros Regulares ou Platônicos Os cinco tipos possíveis de poliedros regulares são o tetraedro, o hexaedro ou cubo, o octaedro, o dodecaedro e o icosaedro. Ë muito interessante observarmos a presença desses poliedros, ou formas poliédricas derivadas, na natureza e na infinita capacidade do engenho humano de copiá-los em estruturas arquitetônicas belíssimas, em objetos, em moléculas e até mesmo na lapidação de pedras preciosas. Na verdade até podemos dizer que o estudo dos poliedros sempre foi um esforço que os os matemáticos, arquitetos, artesões e artistas fizeram no sentido de dominar as relações entre suas formas para poder reproduzi-las e recriar sua estética. Observe a seguir algumas formas que encontramos na natureza e uma geodésica. Investigue a semelhança entre elas e as formas que estudaremos a seguir

DEFINIÇÃO Denomina-se poliedro regular ou de de Platão[1] ao poliedro convexo que satisfaz as seguintes condições: as faces são polígonos regulares; seus ângulos poliédricos congruentes; - todas as faces têm o mesmo número de arestas; - de cada vértice parte o mesmo número de arestas. 1 PLATÃO(427 ac). Filósofo e matemático grego. Ficou conhecido não como matemático, mas como “O Criador de Matemáticos”. Os poliedros regulares foram chamados de “Sólidos Platônicos” devido a maneira pela qual Platão os aplicou para explicar fenômenos científicos. Vejamos a seguir os cinco poliedros regulares

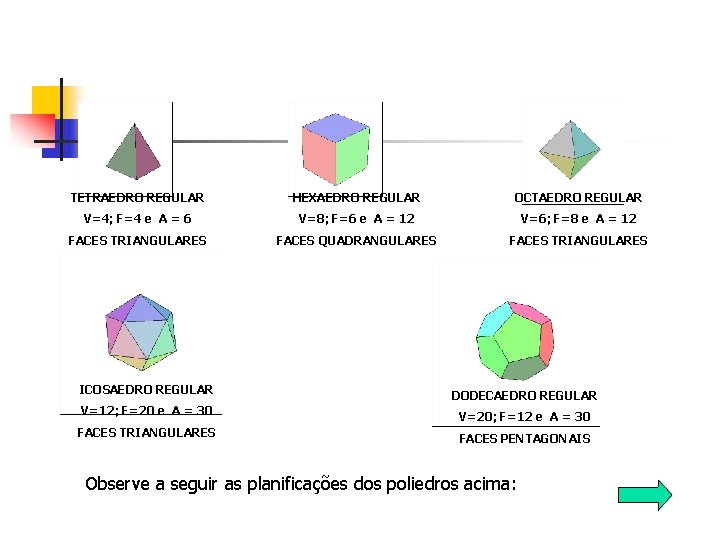
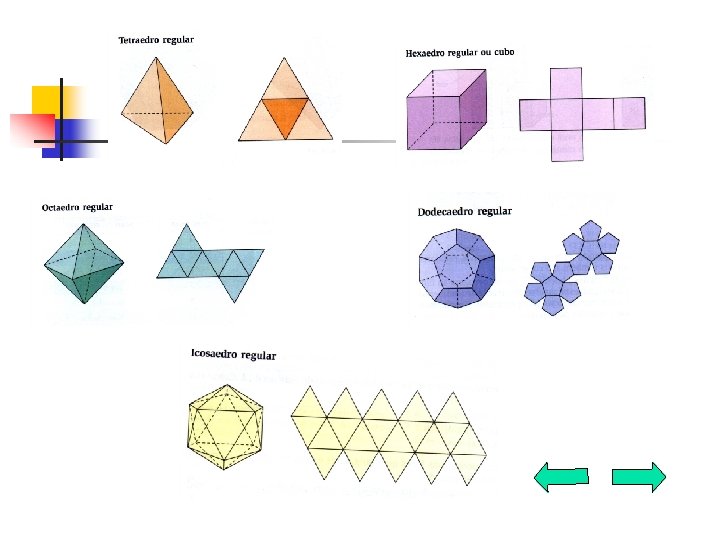
TETRAEDRO REGULAR HEXAEDRO REGULAR OCTAEDRO REGULAR V=4; F=4 e A = 6 V=8; F=6 e A = 12 V=6; F=8 e A = 12 FACES TRIANGULARES FACES QUADRANGULARES FACES TRIANGULARES ICOSAEDRO REGULAR DODECAEDRO REGULAR V=12; F=20 e A = 30 V=20; F=12 e A = 30 FACES TRIANGULARES FACES PENTAGONAIS Observe a seguir as planificações dos poliedros acima:

ATIVIDADES 1) Determinar o número de vértices de um poliedro convexo que tem 2 faces quadrangulares e 8 faces triangulares. Resp: V= 8 2) Determinar o número de faces de um poliedro convexo com 9 vértices. Sabe-se que de 4 vértices partem 3 arestas e dos outros 5 vértices partem 4 arestas. Resp: F = 9 3) Um poliedro convexo tem 14 arestas e 6 faces. Determinar: a) o número de vértices desse poliedro, Resp: 10 b) a soma das medidas dos ângulos das faces desse poliedro. Resp: 2880º 4) Em um poliedro convexo de 20 arestas, o número de faces é igual ao número de vértices. Quantas faces tem esse poliedro ? Resp: 11 faces 5) ( FAAP-SP) Num poliedro convexo, o número de aresta excede o número de vértices em 6 unidades Calcule o número de faces. Resp: 8 faces

ATIVIDADES 6) A soma dos ângulos das faces de um poliedro convexo é 1080º. Determine o número de faces, sabendo que o poliedro tem 8 arestas. Resp: 5 faces 7) Calcule a soma dos ângulos das faces do: a) tetraedro regular Resp: 720º b) octraedro regular Resp: 1440º c) icosaedro regular Resp: 3600º 8) Qual a área da superfície de: a) tetraedro regular de aresta 6 m, Resp: 72 m 2 b) icosaedro regular de aresta 5 cm Resp: 125 cm 2 9) (UNIRIO-RJ) Um geólogo encontrou, numa de suas explorações, um cristal de rocha no formato de um poliedro, que satisfaz a relação de Euler, de 60 faces triangulares. O número de vértices é: a)35 b) 34 c) 33 d) 32 e) 31 Resp: d 10) ( FUVEST-SP) O número de faces triangulares de uma pirâmide é 11. Pode-se, então, afirmar que essa pirâmide possui: a) 33 vértices e 22 arestas b)12 vértices e 11 arestas c)22 vértices e 11 arestas d)11 vértices e 22 arestas e)12 vértices e 22 arestas Resp: e

AULA ELABORADA PELO: n PROF. LUIZ CARLOS S 0 UZA SANTOS É SHOW