Computacin Grfica Transformaciones geomtricas 2 D y 3

Computación Gráfica Transformaciones geométricas 2 D y 3 D Semestre 201321 CRN Septiembre 2012 – Febrero 2013 Ciro Durán Ingeniero en Computación ciro. duran@gmail. com http: //www. ciroduran. com @chiguire Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

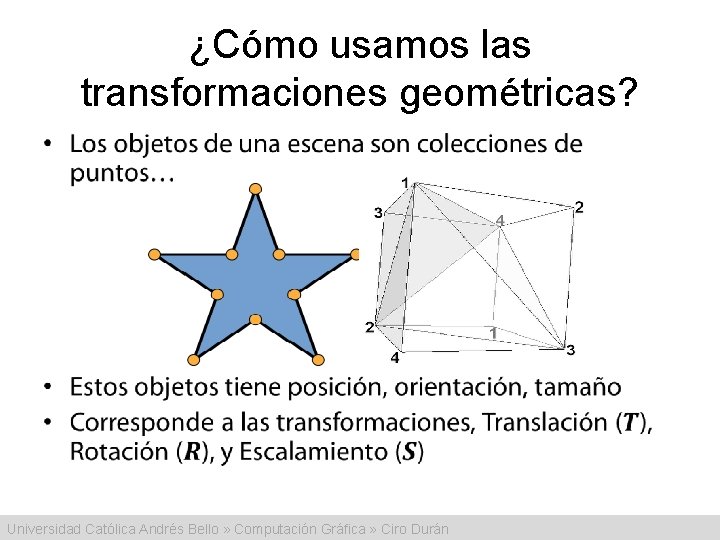
¿Cómo usamos las transformaciones geométricas? • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

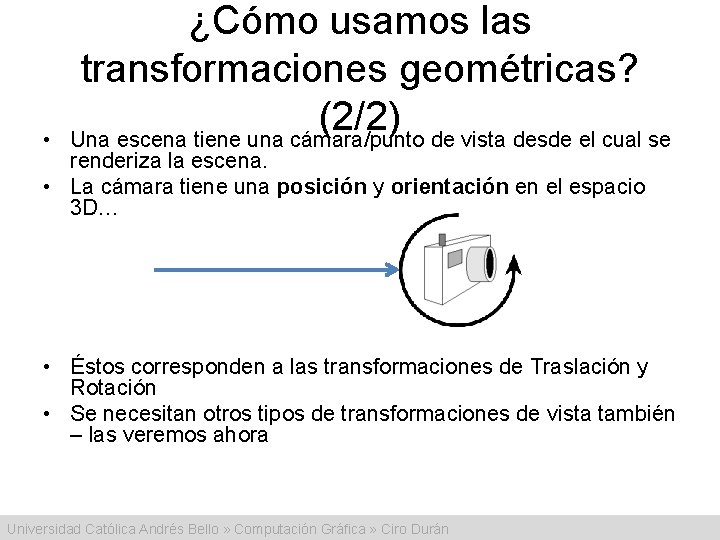
• ¿Cómo usamos las transformaciones geométricas? (2/2) Una escena tiene una cámara/punto de vista desde el cual se renderiza la escena. • La cámara tiene una posición y orientación en el espacio 3 D… • Éstos corresponden a las transformaciones de Traslación y Rotación • Se necesitan otros tipos de transformaciones de vista también – las veremos ahora Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Algunos conceptos de álgebra lineal… • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Transformaciones lineales (1/3) • b a Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Transformaciones lineales (2/3) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

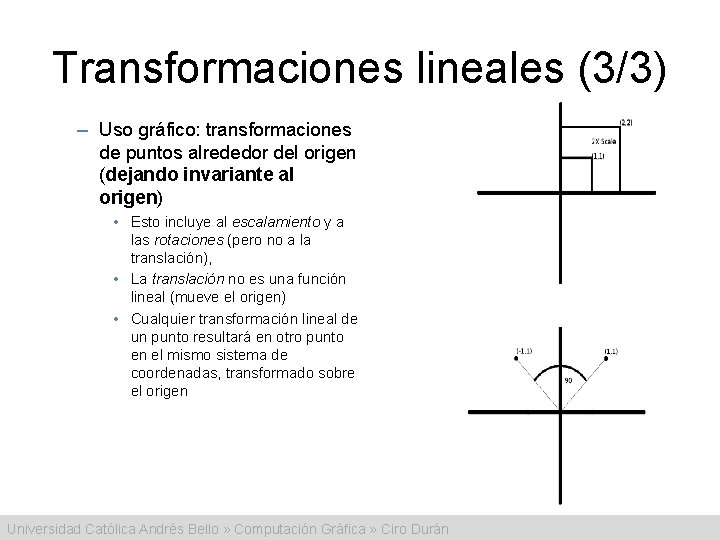
Transformaciones lineales (3/3) – Uso gráfico: transformaciones de puntos alrededor del origen (dejando invariante al origen) • Esto incluye al escalamiento y a las rotaciones (pero no a la translación), • La translación no es una función lineal (mueve el origen) • Cualquier transformación lineal de un punto resultará en otro punto en el mismo sistema de coordenadas, transformado sobre el origen Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Transformaciones lineales como matrices (1/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Transformaciones lineales como matrices (2/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Escalando en 2 D (1/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán Efecto lateral: la casa cambia su posición relativa al origen

Escalando en 2 D (2/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

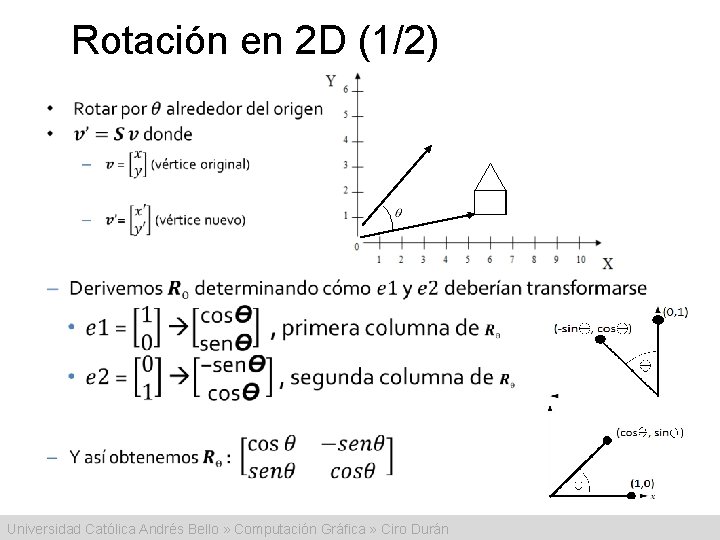
Rotación en 2 D (1/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Rotación en 2 D (2/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

¿Qué hay sobre la traslación? • Si tratamos todas las transformaciones de una manera consistente, es decir, con representación de matrices, entonces podríamos combinar las trnasformaciones al componer sus matrices � Usemos nuevamente una matriz � ¿Cómo? Con coordenadas homogéneas: agrega una dimensión adicional, el eje w, y una coordenada extra, el componente w. � � Y así 2 D -> 3 D (efectivamente el hiperespacio para colocar el espacio 2 D) Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Coordenadas homogéneas (1/3) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Coordenadas homogéneas (2/3) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Coordenadas homogéneas (3/3) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

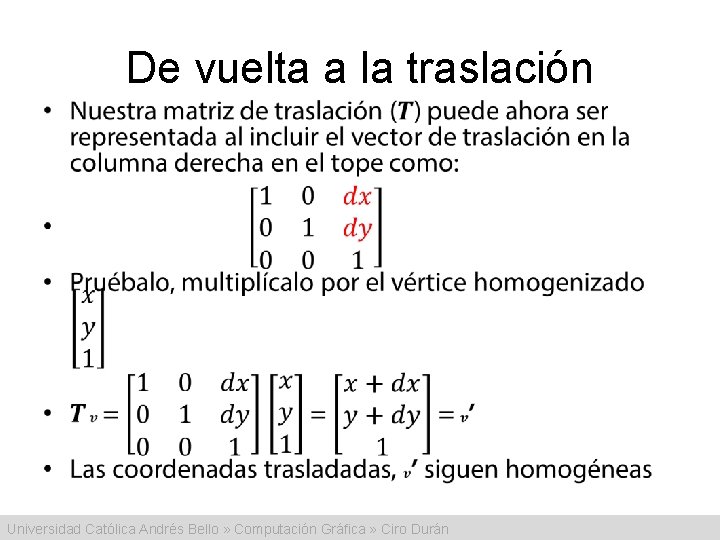
De vuelta a la traslación • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

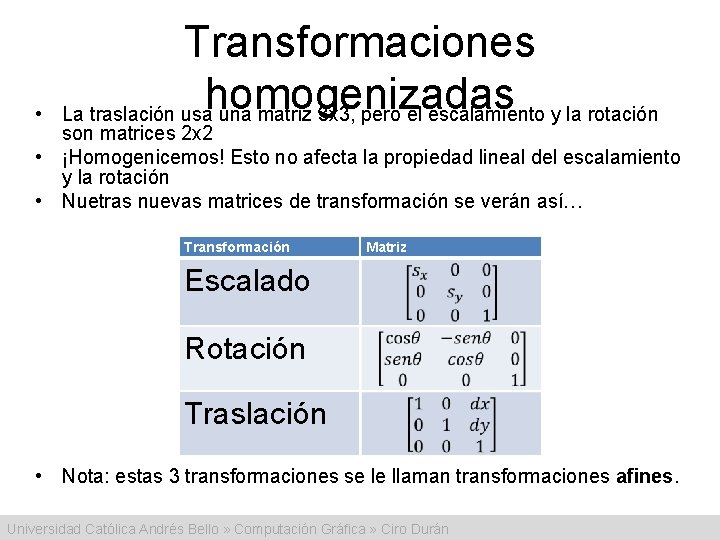
• Transformaciones homogenizadas La traslación usa una matriz 3 x 3, pero el escalamiento y la rotación son matrices 2 x 2 • ¡Homogenicemos! Esto no afecta la propiedad lineal del escalamiento y la rotación • Nuetras nuevas matrices de transformación se verán así… Transformación Matriz Escalado Rotación Traslación • Nota: estas 3 transformaciones se le llaman transformaciones afines. Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Ejemplos • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

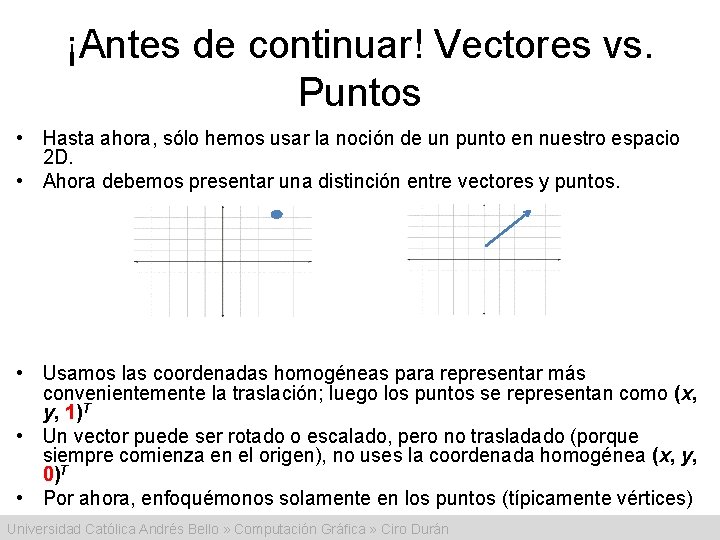
¡Antes de continuar! Vectores vs. Puntos • Hasta ahora, sólo hemos usar la noción de un punto en nuestro espacio 2 D. • Ahora debemos presentar una distinción entre vectores y puntos. • Usamos las coordenadas homogéneas para representar más convenientemente la traslación; luego los puntos se representan como (x, y, 1)T • Un vector puede ser rotado o escalado, pero no trasladado (porque siempre comienza en el origen), no uses la coordenada homogénea (x, y, 0)T • Por ahora, enfoquémonos solamente en los puntos (típicamente vértices) Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Inversas • How do we find the inverse of a transformation? • Take the inverse of the transformation matrix Transformation Matrix Inverse Does it make sense? If you scale something by factor X, the (thanks to homogenization, they’re all invertible!): Scaling inverse is scaling by 1/X Rotation Not so obvious, but can use math! Rotation Matrix is orthonormal, so inverse should just be the transpose, (proof on slide 23) Translation If you translate by X, the inverse is translating by -X Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

More with Homogeneous Coordinates • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

A moment of appreciation for linear algebra • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Composition of Transformations (2 D) (1/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Composition of Transformations (2 D) (2/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

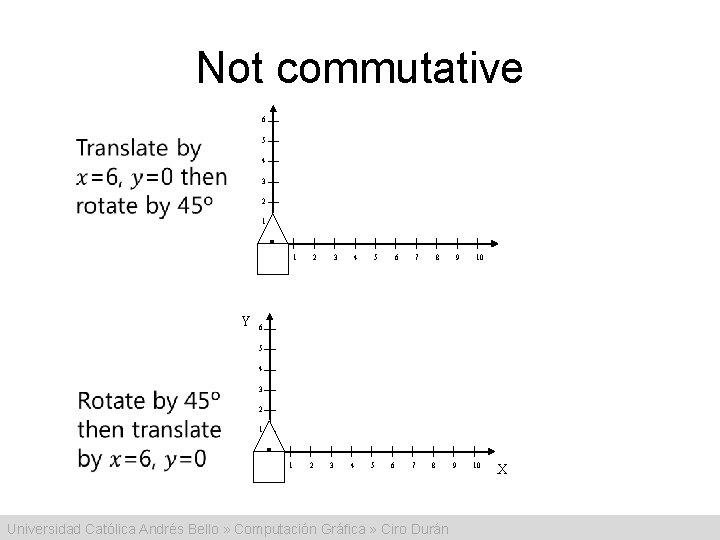
Not commutative 6 5 4 3 2 1 0 1 Y 2 3 4 5 6 7 8 9 10 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 9 10 X

Composition (an example) (2 D) • (1/2) Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

• Composition (an example) (2 D) (2/2) Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

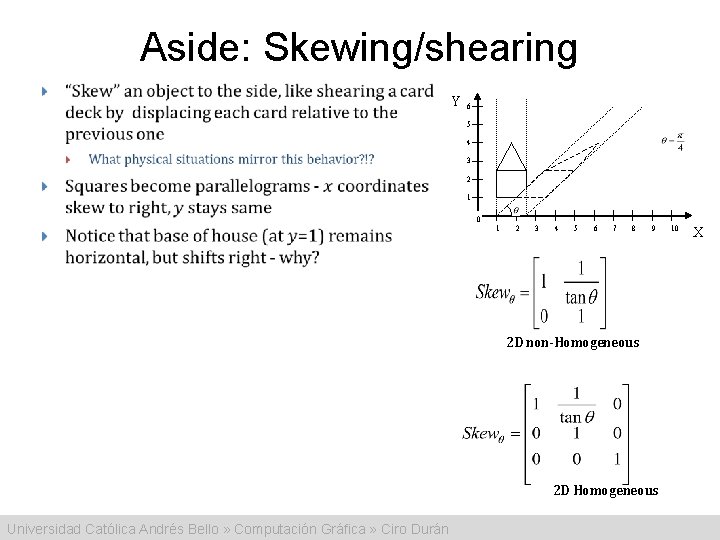
Aside: Skewing/shearing Y 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 2 D non-Homogeneous 2 D Homogeneous Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 10 X

Inverses Revisited • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

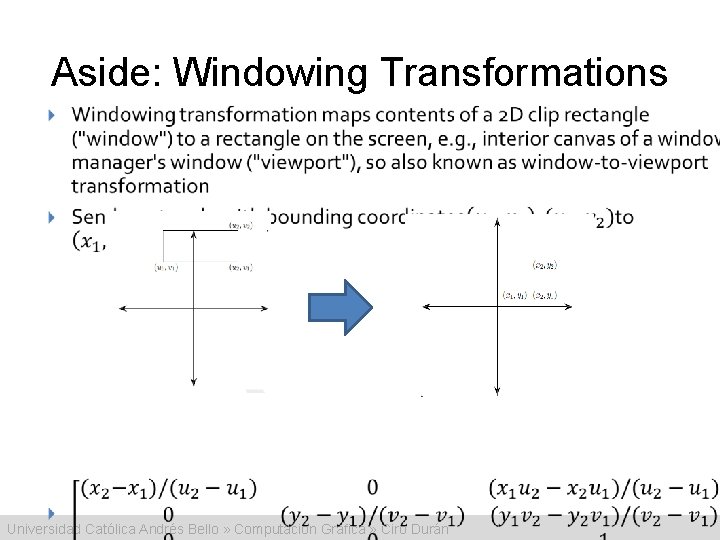
Aside: Windowing Transformations • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

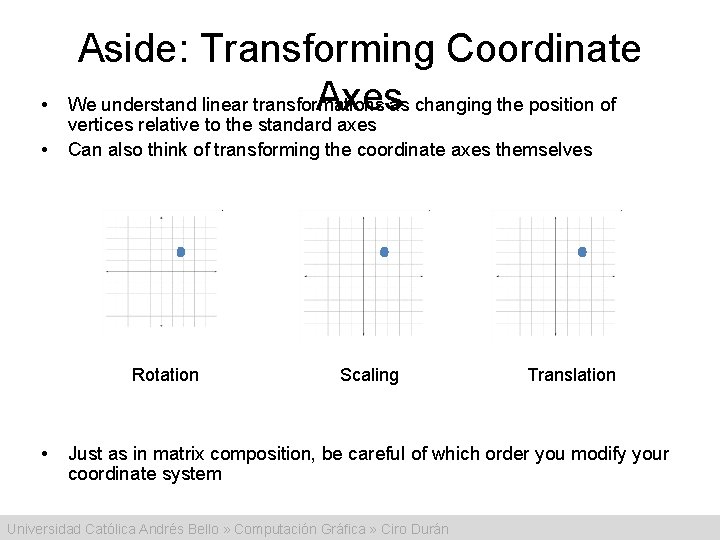
• • Aside: Transforming Coordinate Axes We understand linear transformations as changing the position of vertices relative to the standard axes Can also think of transforming the coordinate axes themselves Rotation • Scaling Translation Just as in matrix composition, be careful of which order you modify your coordinate system Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

Dimension++ (3 D!) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán

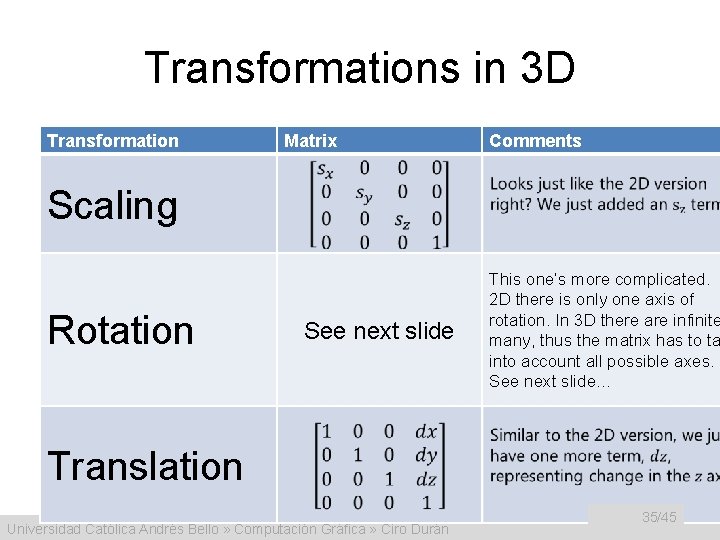
Transformations in 3 D Transformation Matrix Comments Scaling Rotation See next slide This one’s more complicated. I 2 D there is only one axis of rotation. In 3 D there are infinite many, thus the matrix has to ta into account all possible axes. See next slide… Translation Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 35/45

Rodrigues’s Formula… • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 36/45

• Rotating axis by axis (1/2) Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 37/45

Rotating axis by axis (2/2) • Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 38/45

Inverses and Composition in 3 D! • Inverses are once again parallel to their 2 D versions… Transformation Matrix Inverse Scaling Rotation • Composition works exactly the same way… Translation Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 39/45

• Example in 3 D! Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 40/45

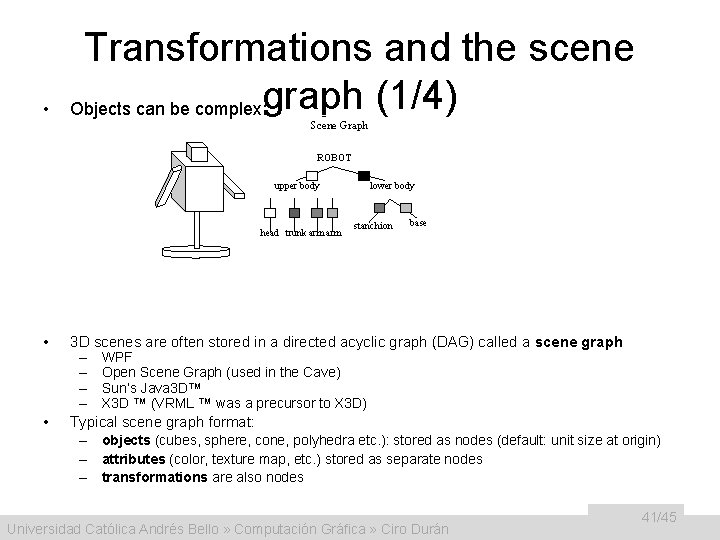
• Transformations and the scene Objects can be complex: graph (1/4) Scene Graph ROBOT upper body head trunk arm • • lower body stanchion base 3 D scenes are often stored in a directed acyclic graph (DAG) called a scene graph – WPF – Open Scene Graph (used in the Cave) – Sun’s Java 3 D™ – X 3 D ™ (VRML ™ was a precursor to X 3 D) Typical scene graph format: – objects (cubes, sphere, cone, polyhedra etc. ): stored as nodes (default: unit size at origin) – attributes (color, texture map, etc. ) stored as separate nodes – transformations are also nodes Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 41/45

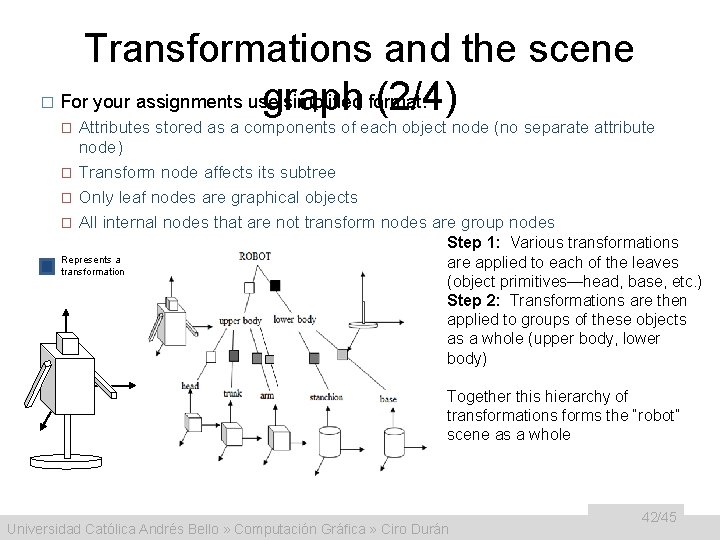
� Transformations and the scene For your assignments use simplified format: graph (2/4) � � Attributes stored as a components of each object node (no separate attribute node) Transform node affects its subtree Only leaf nodes are graphical objects All internal nodes that are not transform nodes are group nodes Represents a transformation Step 1: Various transformations are applied to each of the leaves (object primitives—head, base, etc. ) Step 2: Transformations are then applied to groups of these objects as a whole (upper body, lower body) Together this hierarchy of transformations forms the “robot” scene as a whole Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 42/45

Transformations and the scene • graph (3/4) object nodes (geometry) transformation nodes group nodes Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán 43/45

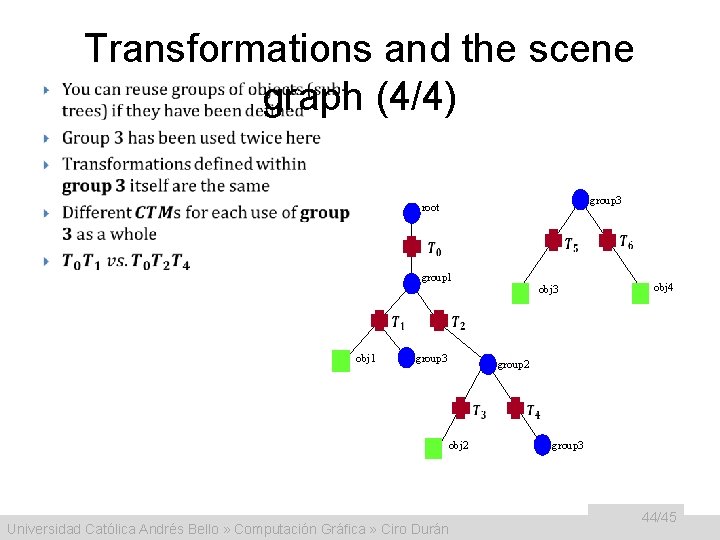
Transformations and the scene • graph (4/4) group 3 root group 1 obj 1 obj 3 obj 4 group 3 group 2 obj 2 Universidad Católica Andrés Bello » Computación Gráfica » Ciro Durán group 3 44/45